关于熵的一些数学知识

本文主要是介绍关于熵的一些数学知识，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一些信息熵的含义

(1)   信息熵的定义：假设X是一个离散随即变量，即它的取值范围R={x₁，x₂...}是有限可数的。设p_i=P{X=x_i}，X的熵定义为：

                                               (a)

若(a)式中，对数的底为2，则熵表示为H₂(x)，此时以2为基底的熵单位是bits，即位。若某一项p_i=0，则定义该项的p_ilogp_i^-1为0。

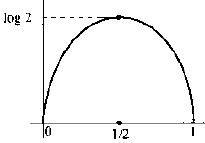
(2)   设R={0,1}，并定义P{X=0}=p，P{X=1}=1-p。则此时的H(X)=-plogp-(1-p)log(1-p)。该H(x)非常重要，称为熵函数。熵函数的的曲线如下图表示：

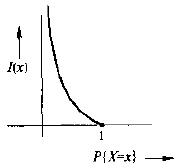
再者，定义对于任意的x∈R，I(x)=-logP{X =x}。则H(X)就是I(x)的平均值。此时的I(x)可视为x所提供的信息量。I(x)的曲线如下：

(3)   H(X)的最大值。若X在定义域R={x₁,x₂,...x_r}，则0<=H(X)<=logr。

(4)   条件熵：定义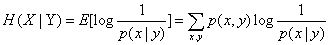

推导：H(X|Y=y)= ∑p(x|y)log{1/p(x,y)}

H(X|Y)=∑p(y)H(X|Y=y)= ∑p(y)*∑p(x|y)log{1/p(x/y)}

       H(X|Y)表示得到Y后，X的平均信息量，即平均不确定度。

(5)   Fano不等式：设X和Y都是离散随机变量，都取值于集合{x₁,x₂,...x_r}。则

H(X|Y)<=H(Pe)+Pe*log(r-1)

其中Pe=P{X≠Y}。Fano表示在已经知道Y后，仍然需要通过检测X才能获得的信息量。检测X的一个方法是先确定X=Y。若X=Y，就知道X；若X≠Y，那么还有r-1个可能。

(6)   互信息量：I(X;Y)=H(X)-H(X|Y)。I(X;Y)可以理解成知道了Y后对于减少X的不确定性的贡献。

来源：http://blog.csdn.net/kxy_tech/article/details/3993457

I(X;Y)的公式：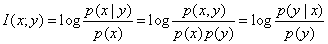

I(X;Y)=∑_(x,y)p(x,y)log{p(y|x)/p(y)}

 

(7)   联合熵定义为两个元素同时发生的不确定度。

联合熵H(X,Y)= ∑_(x,y)p(x,y)logp(x,y)=H(X)+H(Y|X)

 

(8)   信道中互信息的含义

互信息的定义得：

I(X,Y)=H(X)-H(X|Y)= I(Y,X)=H(Y)-H(Y|X)

若信道输入为H(X)，输出为H(Y)，则条件熵H(X|Y)可以看成由于信道上存在干扰和噪声而损失掉的平均信息量。条件熵H(X|Y)又可以看成由于信道上的干扰和噪声的缘故，接收端获得Y后还剩余的对符号X的平均不确定度，故称为疑义度。

条件熵H(Y|X)可以看作唯一地确定信道噪声所需要的平均信息量，故称为噪声熵或者散布度。

(9)   I(X,Y)的重要结论

互信息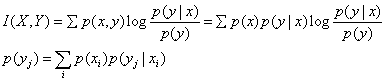 

互信息I(X,Y)只是输入信源X的概率分布P(x_i)和信道转移概率P(y_j|x_i)的函数，可以证明当P(x_i)一定时，I是关于P(y_j|x_i)的∪函数，存在极小值；当P(y_j|x_i)一定时，I是关于P(x_i)的∩函数，存在极大值。

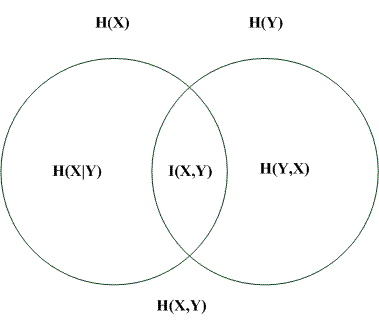
(10)   联合熵、条件熵的关系图。H(X)>=H(X|Y)，H(Y)>=H(Y|X)。

 

 

 

这篇关于关于熵的一些数学知识的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---