本文主要是介绍【重拾数学知识】导数、极值和最值,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
在深度学习中,梯度下降法是一种常用的优化算法,用于更新模型参数以最小化损失函数。这梯度下降法中涉及到数学中的导数、极值等相关知识,因此我们重新回顾相关内容,以便加深理解。
相关概念
导数
一个问题
如何求得一个曲线f(x)中任意一点(x0)的斜率?
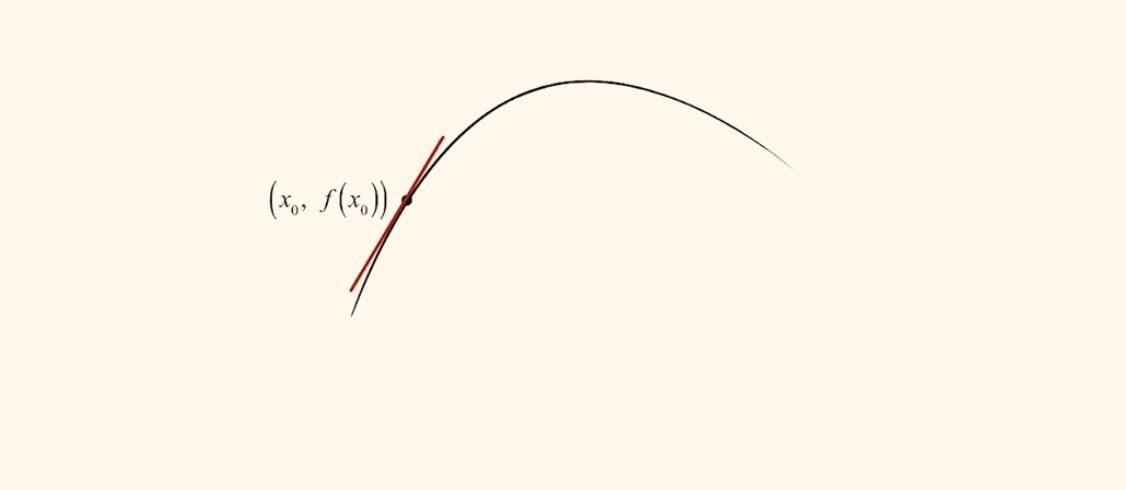
核心思想:在曲线上另外存在一个P点,P点无限接近x0,x0和P的连线将无限接近x0点的斜率。
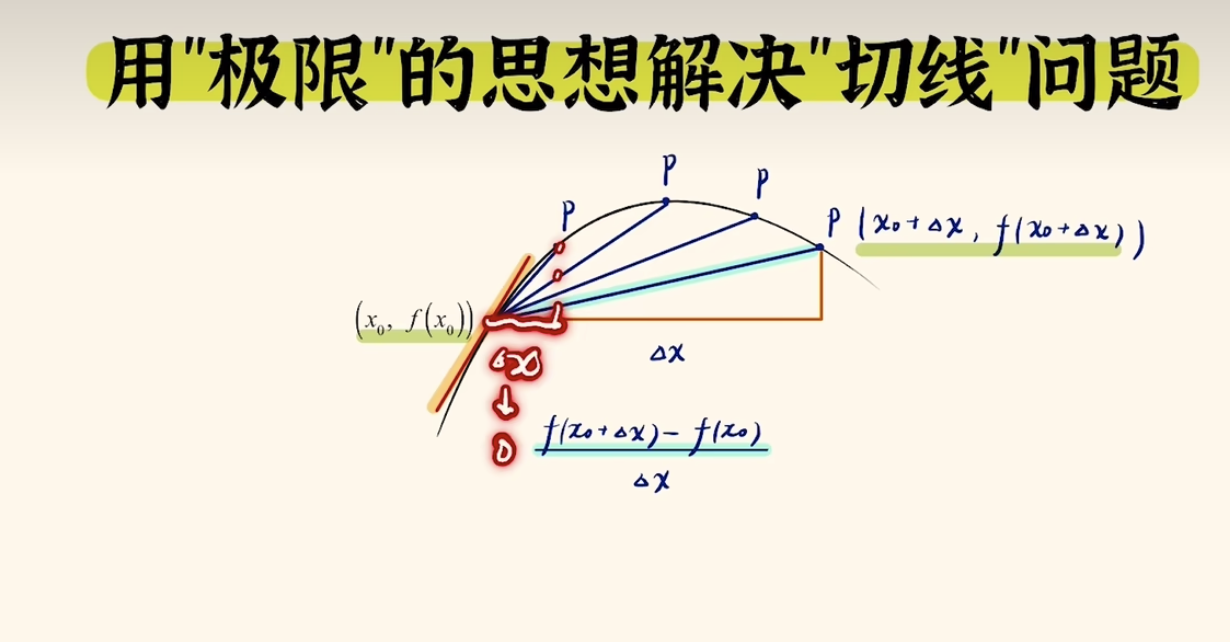
在上图中:
-
我们求x0点和P点的之间的斜率为:
斜率公式:
k = y 1 − y 2 x 1 − x 2 = f ( x 0 + Δ x ) − f ( x 0 ) Δ x k = \frac{y_1-y_2}{x_1-x_2} = \frac{f(x_0+Δx) - f(x_0)}{Δx} k=x1−x2y1−y2=Δxf(x0+Δx)−f(x0)
-
加入极限条件Δx→0趋近于0时
f ′ ( x ) = l i m ( Δ x − > 0 ) f ( x + Δ x ) − f ( x ) Δ x f'(x) = lim(Δx->0) \frac{f(x + Δx) - f(x)}{Δx} f′(x)=lim(Δx−>0)Δxf(x+Δx)−f(x)
定义
导数表示函数 f(x) 在某一点 x 处的变化率(或斜率),通常记作 f’(x) 或 df/dx。
常见求导公式

偏导
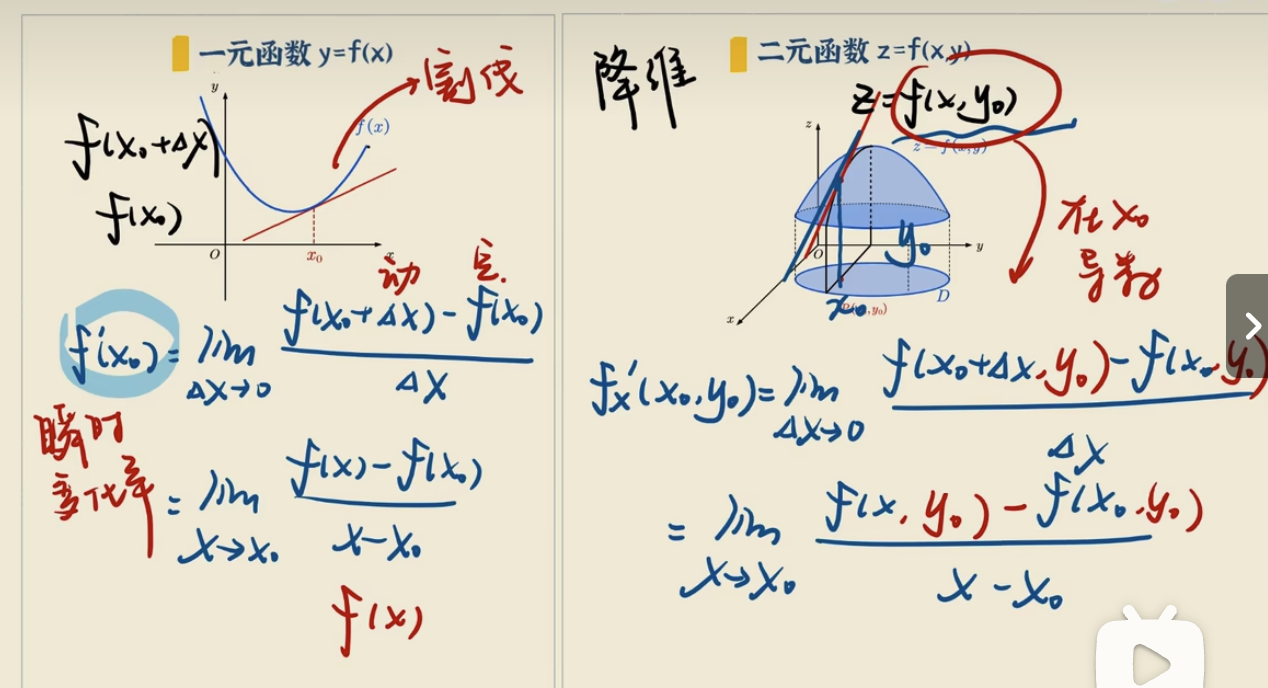
接着,我们看下什么是偏导。如下图所示:
- 在左侧的二维平面中,一元函数f(x)在x0的导数为x0点的斜率,即为导数;
- 在右侧的三维空间中,二元函数z = f(x,y),在固定住y坐标轴(即:y=y0,如图中黑色线段向下切所示)时,求z=f(x, y0)在x0的导数,即为
偏导数。
定义
-
偏导数是多元函数在某一点上对某个特定变量的导数,即函数在该点上沿着某个坐标轴方向的变化率。
偏导数本质上是在多元函数中,通过固定某一变量为常量,将多元降维。
极值与最值
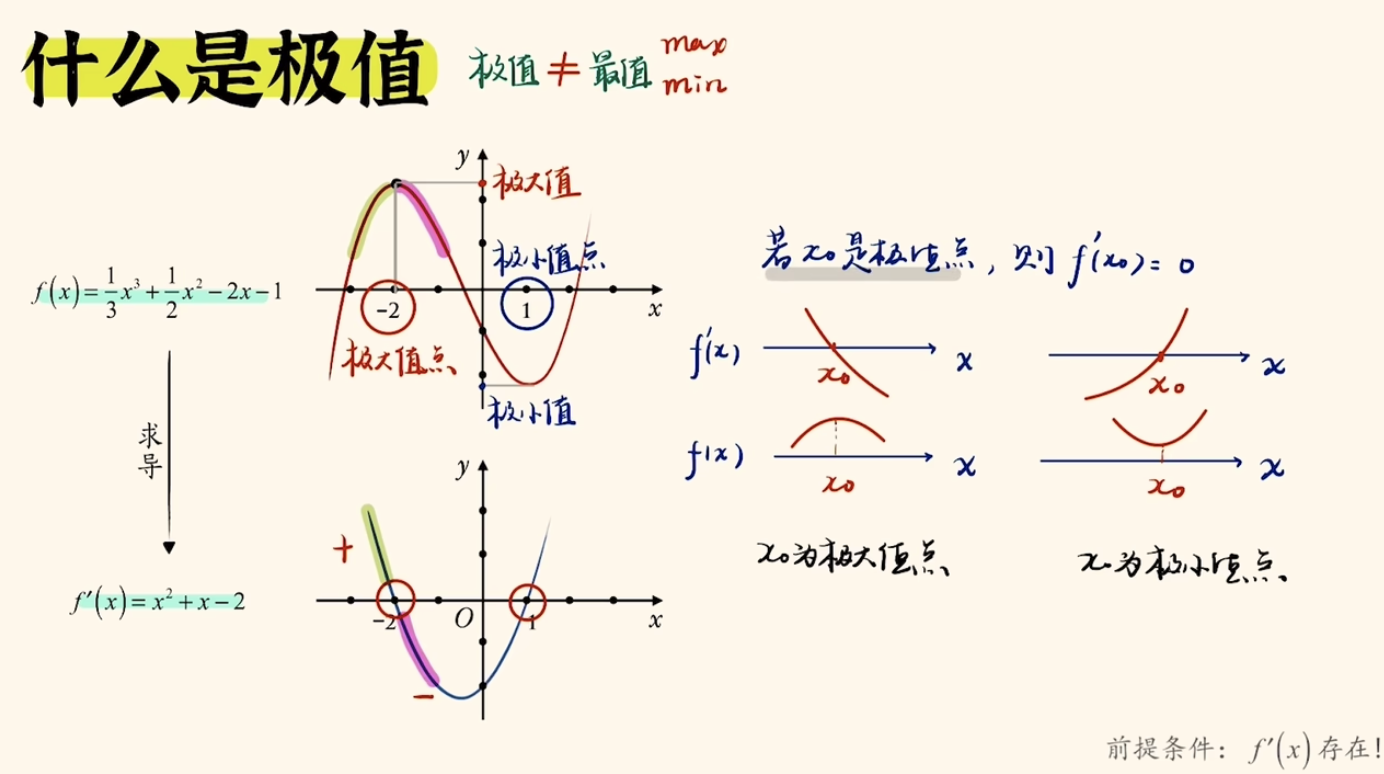
在下面图例函数中,
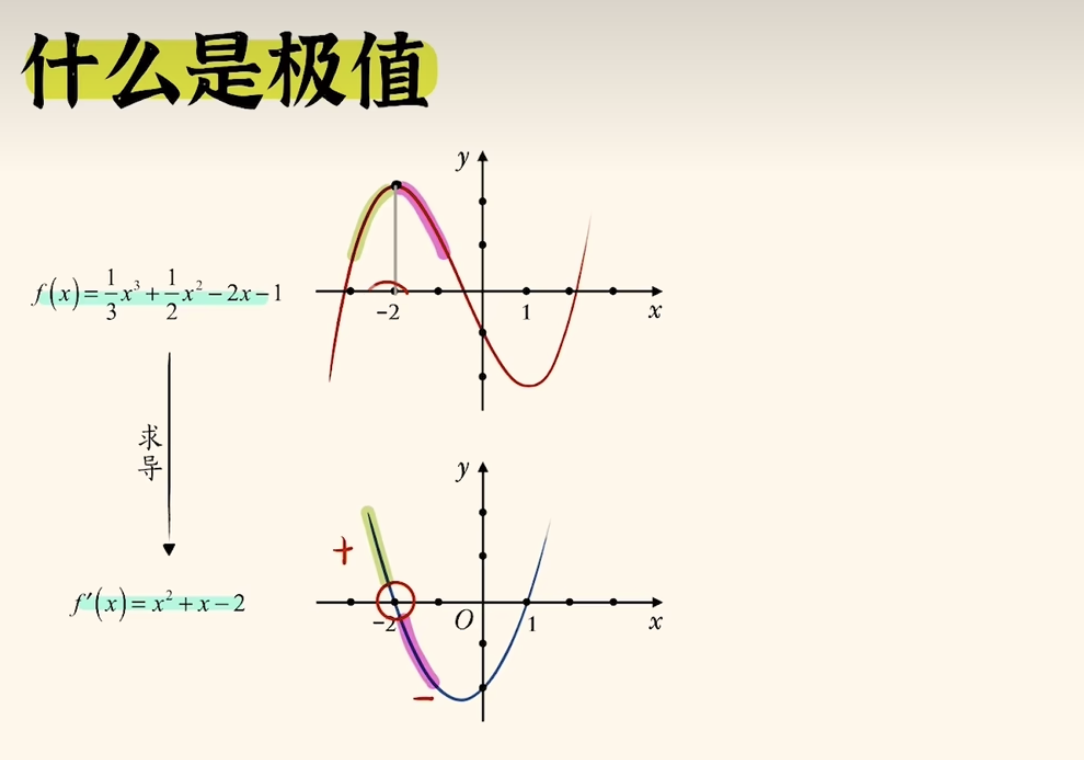
f ( x ) = 1 3 x 3 + 1 2 x 2 − 2 x − 1 f(x) = \frac{1}{3}x^3 + \frac{1}{2}x^2 - 2x - 1 f(x)=31x3+21x2−2x−1
通过求导,得到导数为
f ′ ( x ) = x 2 + x − 2 f'(x) = x^2 + x -2 f′(x)=x2+x−2
其中:
-
解方程f’(x) = 0,得到极值点为 x = -2 和 x = 1
-
当x = -2时,f’(x) < 0;
-
当x = 1 时,f’(x) > 0;
-
也就是说:x=-2的左侧是
单调递增,x=-2到x=1之间是单调递减,x=-2这个点比左边要高,比右侧也要高,我们把这种点成为极值点。
-
定义
-
极值是函数在某一点或某一区间内取得的最大值或最小值。极大值是函数在该点附近取得的最大值,极小值是函数在该点附近取得的最小值。
-
最值是函数在定义域内取得的最大值或最小值。最大值是函数在整个定义域内取得的最大值,最小值是函数在整个定义域内取得的最小值。
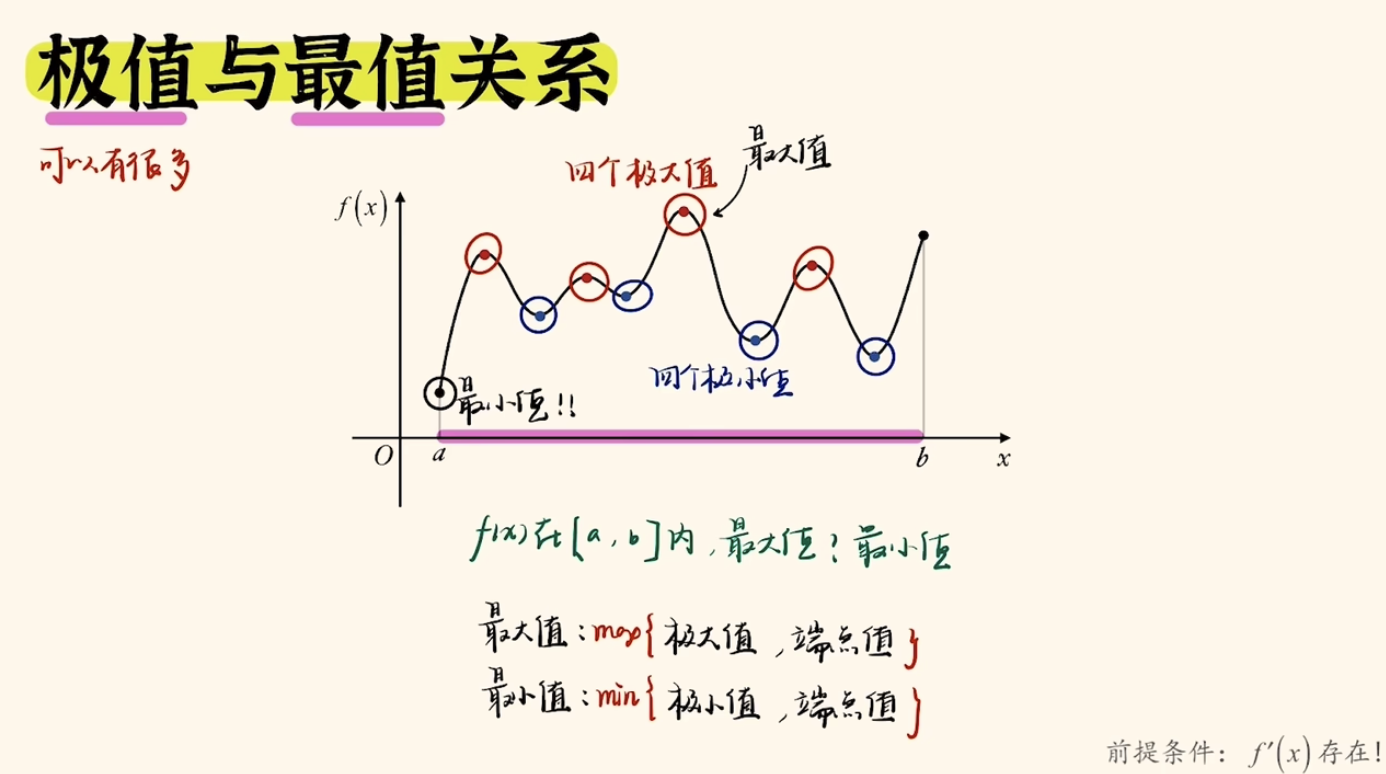
特别注意:极值≠最值;一个曲线在一段区间内,可能有多个极值,但最值只有一个。
极大值和极小值
若x0是极值点,则f’(x0) = 0,这种情况下有两种可能:
- 若导函数由正往负,那么对应原函数先增后减,那么x0为极大值点。
- 若导函数由负往正,那么对应原函数先减后增,那么x0为极小值点。
参考资料
B站:《"导数"一课通!1h零基础上手》
B站:《“偏导数”一课通!1h零基础上手!|高数下》
这篇关于【重拾数学知识】导数、极值和最值的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





![libtorch---day03[自定义导数]](https://i-blog.csdnimg.cn/direct/c8ee5b1bbf704efa8c035a1bd5d77634.png)

