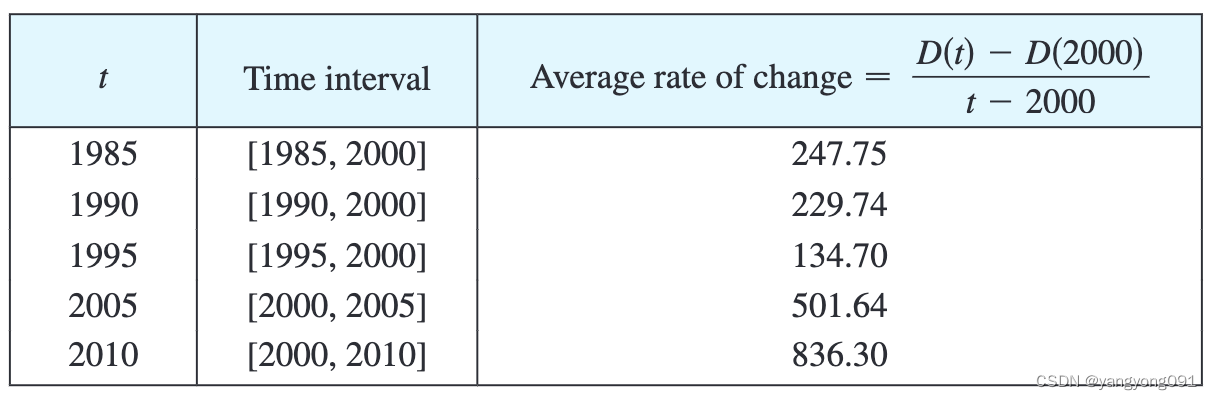
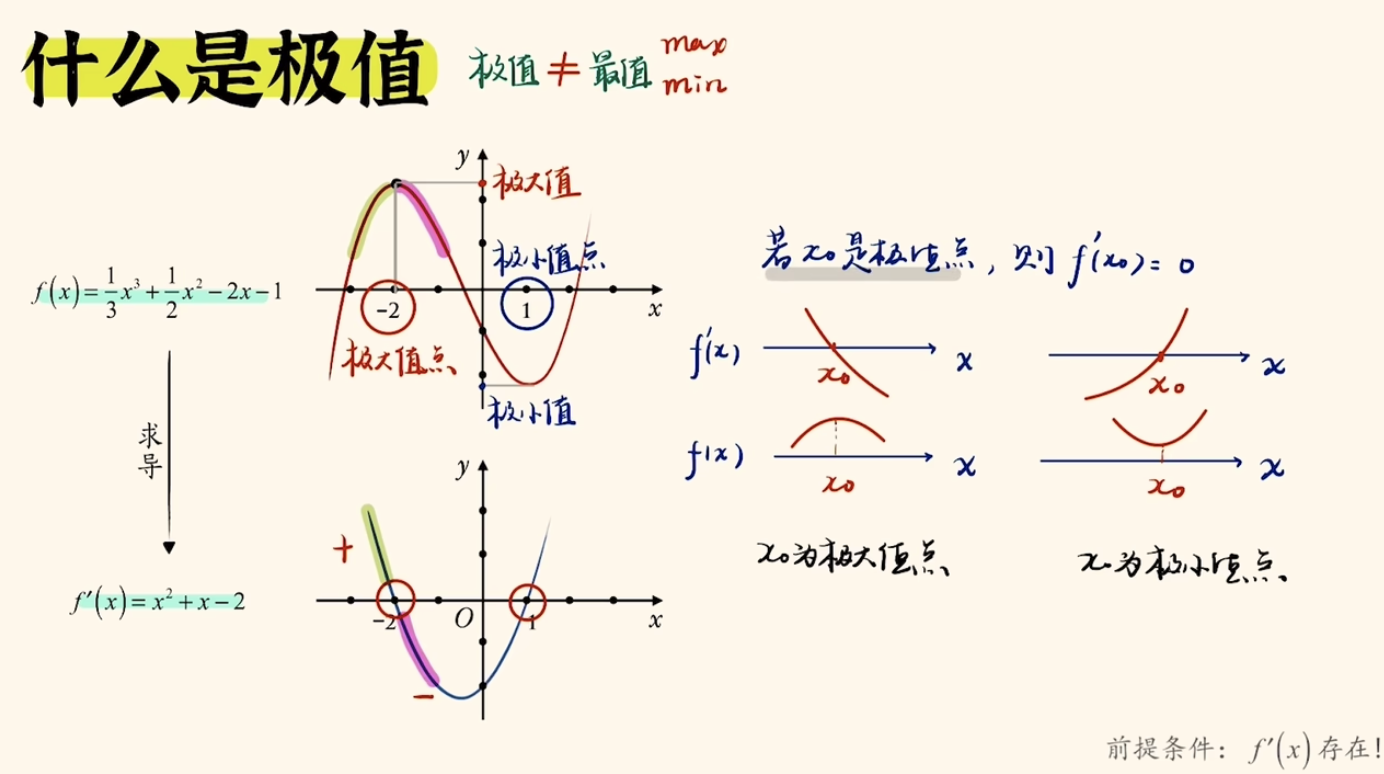
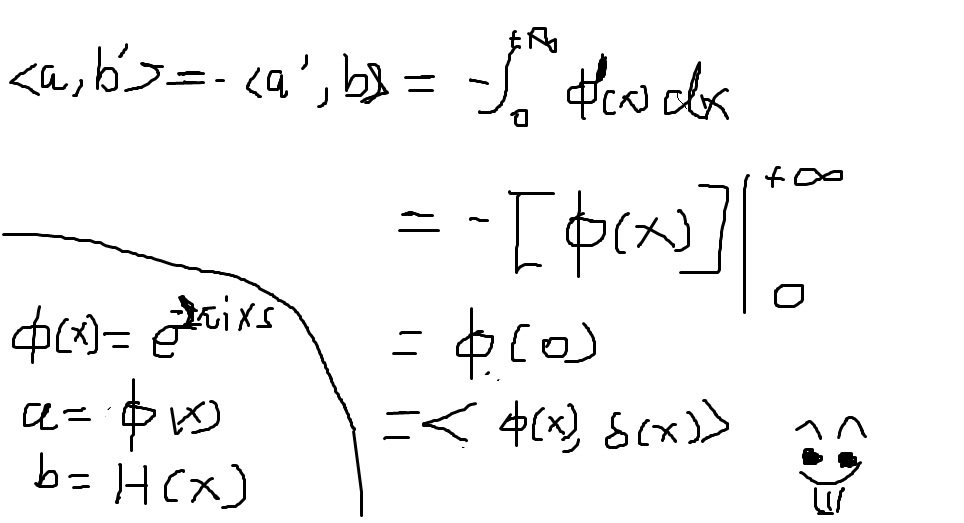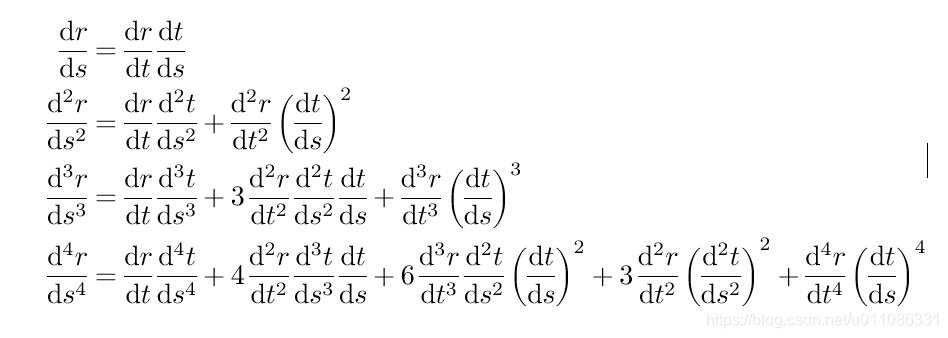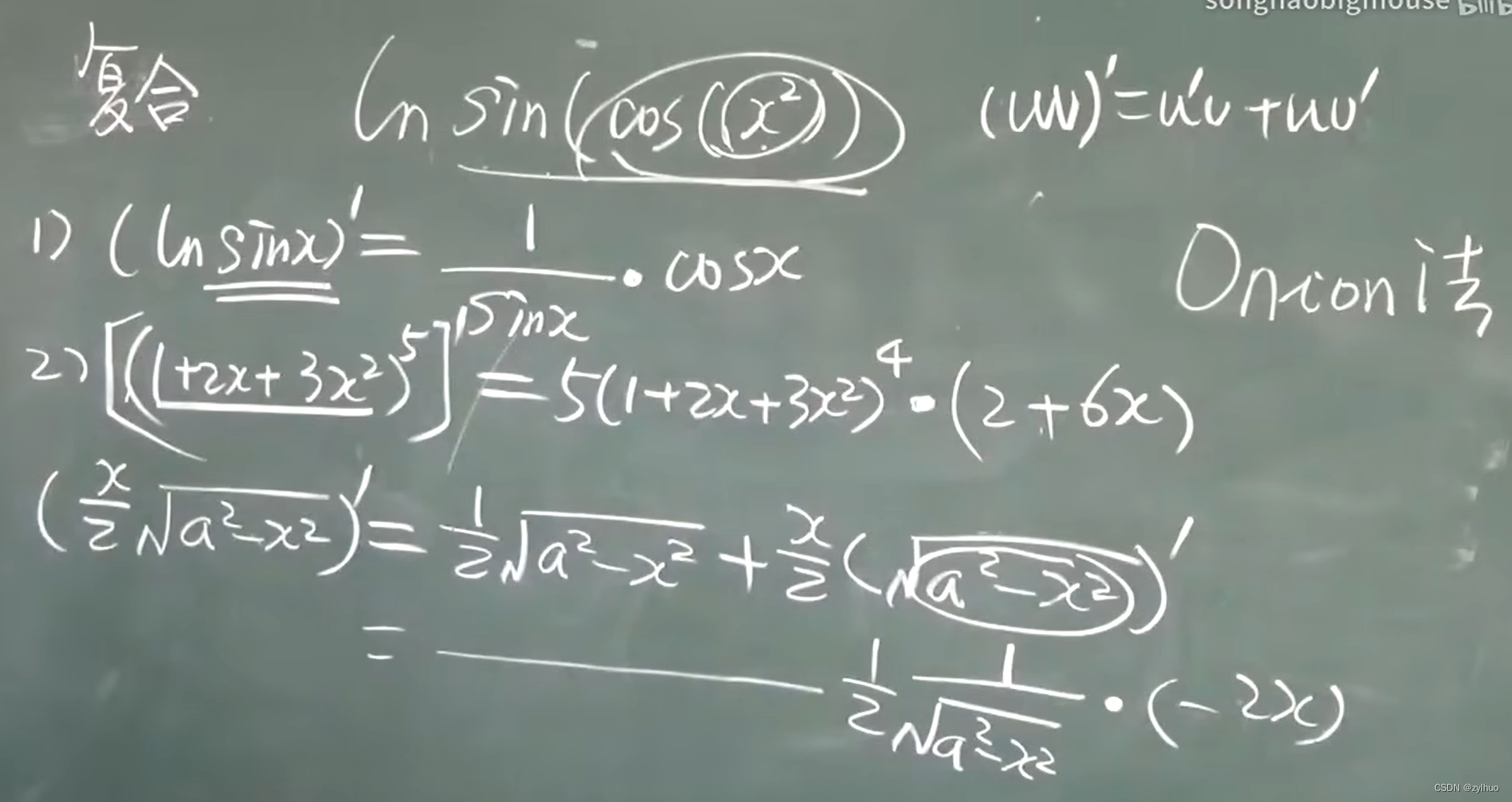导数专题
激活函数 Sigmod 及其导数
文章目录 1. Sigmod 函数2. 取值3. 图像4. 导数 1. Sigmod 函数 Sigmod 函数是神经网络中最常用的激活函数之一，其形式如下： sigmod ( x ) = f ( x ) = 1 1 + e − x . \text{sigmod}(x) = f(x) = \frac{1}{1 + e^{-x}}. sigmod(x)=f(x)=1+e−x1.
![libtorch---day03[自定义导数]](https://i-blog.csdnimg.cn/direct/c8ee5b1bbf704efa8c035a1bd5d77634.png)
libtorch---day03[自定义导数]
参考pytorch。 背景 希望使用勒让德多项式拟合一个周期内的正弦函数。 真值： y = s i n ( x ) , x ∈ [ − π , π ] y=sin(x),x\in\left[-\pi,\pi\right] y=sin(x),x∈[−π,π] torch::Tensor x = torch::linspace(-M_PI, M_PI, 2000, torch::kFloat);
2.3导数与微分的基础与应用
1. 导数的基本概念 大家好，欢迎来到我们的数学大讲堂！今天我们要聊聊一个有点酷又有点恐怖的东西——导数。别担心，不是让你在黑板上画曲线的那种，而是关于“变化率”的一种数学表达。 那么，什么是导数呢？想象一下，你在开车，导数就是告诉你每一秒你的车速变化有多快。比如说，你踩了油门，车速从30公里/小时变到40公里/小时，那导数就是“哟，这小子踩油门了，车速快了！”简单来说，导数就是描述某样东西变
考研数学 高等数学----导数应用
核心框架 前置知识 正式内容 知识点1: 知识点2: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识点: 知识
导数的基本法则与常用导数公式的推导
目录 n 次幂函数导数公式的推导导数和的运算法则的证明正弦、余弦函数导数公式的推导代数证明两个重要极限（引理）及证明具体推导 几何直观 导数积的运算法则的证明导数商的法则的证明链式法则的证明有理幂函数求导法则的证明反函数求导法则的证明反正切函数导数公式的推导指数函数导数公式的推导引入证明第一种方法：代入消元第二种方法：对数微分 幂指函数导数公式的推导幂法则（The Power Rule）的
微积分-导数1（导数与变化率）
切线 要求与曲线 C C C相切于 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))点的切线，我们可以在曲线上找到与之相近的一点 Q ( x , f ( x ) ) Q(x, f(x)) Q(x,f(x))，然后求出割线 P Q PQ PQ的斜率： m P Q = f ( x ) − f ( a ) x − a m_{PQ} = \frac{f(x) - f(a)}
线性代数|机器学习-P16矩阵A的导数
文章目录 1. 概述2. 求 d A − 1 ( t ) d t \frac{\mathrm{d}A^{-1}(t)}{\mathrm{d}t} dtdA−1(t)3. 求 d λ ( t ) d t \frac{\mathrm{d}\lambda(t)}{\mathrm{d}t} dtdλ(t)3.1 A 和 A T A^T AT有相同的特征值3.2 特征向量单位化3.3 求 λ (
梯度，方向导数，相关概念
1. http://blog.cvmarcher.com/posts/2015/06/27/gradient-descent/ 梯度下降法是求解神经网络的方法中最流行的一个，思想很简单，就是函数沿着梯度的方向下降的最快。通常来讲，我们在求解机器学习问题的时候，都会定义一个目标函数，然后基于这个目标函数又定义出损失函数，通过最小化损失函数来使得目标函数达到最优。那么在最小化损失函
高等数学笔记（三）：导数
一、导数概念 1.1 导数的定义 1.1.1 函数在一点处的导数与导函数 1.1.2 单侧导数 1.2 导数的几何意义 1.3 函数可导性与连续性的关系 二、函数的求导法则 2.1 函数的和、差、积、商的求导法则 2.2 反函数的求导法则 2.3 复合函数的求导法则 2.4 基本求导法则与导数公式 三、高阶导数 四、隐函数及由参数
导数应用（一）：差分计算（导数）
导数应用（一）：差分计算（导数） 1.数学背景2.代码 1.数学背景 导数： d y d x = y ( x i ) − y ( x i − 1 ) x i − x x − i \frac{dy}{dx} = \frac{y(x_i) - y(x_{i-1})}{x_i - x_{x-i}} dxdy=xi−xx−iy(xi)−y(xi−1) 差分： Δ Y Δ X
【重拾数学知识】导数、极值和最值
前言 在深度学习中，梯度下降法是一种常用的优化算法，用于更新模型参数以最小化损失函数。这梯度下降法中涉及到数学中的导数、极值等相关知识，因此我们重新回顾相关内容，以便加深理解。 相关概念 导数 一个问题 如何求得一个曲线f(x)中任意一点(x0)的斜率？ 核心思想：在曲线上另外存在一个P点，P点无限接近x0，x0和P的连线将无限接近x0点的斜率。 在上图中： 我们求x0点和
阶跃函数的导数为什么是冲击函数 The derivative of heaviside step function is delta function
如果我今天没搞懂这个，我估计我会抑郁到不能睡觉。 heaviside step function 就是所谓的阶跃函数： 定义 图像： dirac delta function 狄利克雷函数，通常所说的冲击函数： 定义： 函数图像： 提出问题: 为什么heaviside step 函数的导数就是 dirac delta 函数呢？ 感觉上是挺“靠谱”
C语言编程实现导数运算：深入探索与实战解析
C语言编程实现导数运算：深入探索与实战解析 在数学的广袤领域中，导数运算扮演着至关重要的角色，它描述了函数值随自变量变化的速率。然而，将这一理论应用于实际编程中，尤其是使用C语言，却是一项充满挑战的任务。本文将深入探讨C语言编程实现导数运算的四个方面、五个方面、六个方面和七个方面，带您领略其中的奥秘与魅力。 四个方面：导数运算的基本概念与C语言实现 首先，我们需要明确导数运算的基本概念。导数
变上限积分无穷小比阶与导数的关系问题
变上限积分无穷小比阶与导数的关系问题 @(微积分) （2004）把 x→0+ x\rightarrow 0^+时的无穷小 α=∫x0cost2dt,β=∫x20tant√dt,γ=∫x</
Beamer中二阶导、一阶导数的显示问题
Beamer中二阶导、一阶导数的显示问题 解决方法: 最简单的解法方法就是把\documentclass[professionalfont]{beamer} 改为 \documentclass[professionalfont]{beamer} 如果不能解决、请继续阅读查看其他解法 在beamer中表示 f ′ f' f′和 f ′ ′ f'' f′′时发现导数符号距离 f f
Mathematica 怎么列表展示出复合函数高阶导数公式 Faà di Bruno's formula 关于Mathematica推公式的一些技巧等
来自于群友的问题again 如图： 很明显用D就可以解决，但是还要让麦酱认出r和t是复合函数，所以要带上自变量，对于t来说自变量是s，自然写成t[s]，而r是复合函数，直接套着写就行了~ D[r[t[s]],{s,#}]&/@Range@4 代码就写完了，但是输出不符合阅读习惯，看着很头疼啊，比较一下，还是t[s]的问题，写成t就舒服多了 已经可以读了嗯，但是不要忘了麦酱的排版能力，
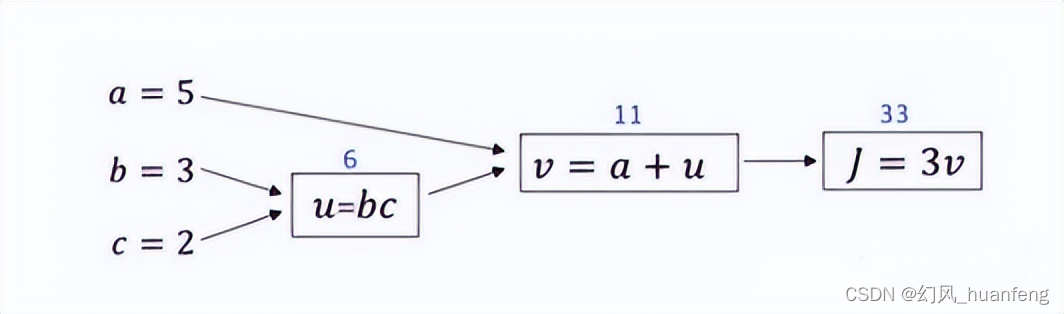
每天五分钟深度学习：如何使用计算图来反向计算参数的导数？
本文重点 在上一个课程中，我们使用一个例子来计算函数J，也就相当于前向传播的过程，本节课程我们将学习如何使用计算图计算函数J的导数。相当于反向传播的过程。 计算J对v的导数，dJ/dv=3 计算J对a的导数，dJ/da=（dJ/dv）*（dv/da）=3*1=3 计算J对u的导数，dJ/du=（dJ/dv）*（dv/du）=3*1=3 计算J对b的导数，dJ/db=(dJ/dv)*(
激活函数原函数和导数的绘制及饱和度-- 021
微信公众号：python宝关注可了解更多的python相关知识。若有问题或建议，请公众号留言; 内容目录 一、激活函数简介二、Sigmoid三、tanh四、ReLU 五、其它激活函数及饱和度 一、激活函数简介 深度学习的发展一般分为三个阶段，感知机-->三层神经网络-->深度学习（表示学习）。早先的感知机由于采用线性模型，无法解决异或问题，表示能力受到限制。为此三层神经网络
理解导数（x^n求导后nx^n-1）
以下都是为了方便理解 微小量是 t M(x)是一个函数 M 在 x 处的斜率 = M 在 x 处的导数 = 垂直距离 平移距离 = M ( x + t ) − M ( x ) ( x + t ) − x M在x处的斜率 = M在x处的导数= \dfrac{垂直距离}{平移距离} =\dfrac{M\left( x+t\right) -M\left( x\right) }{(x + t)
