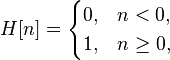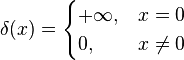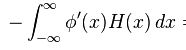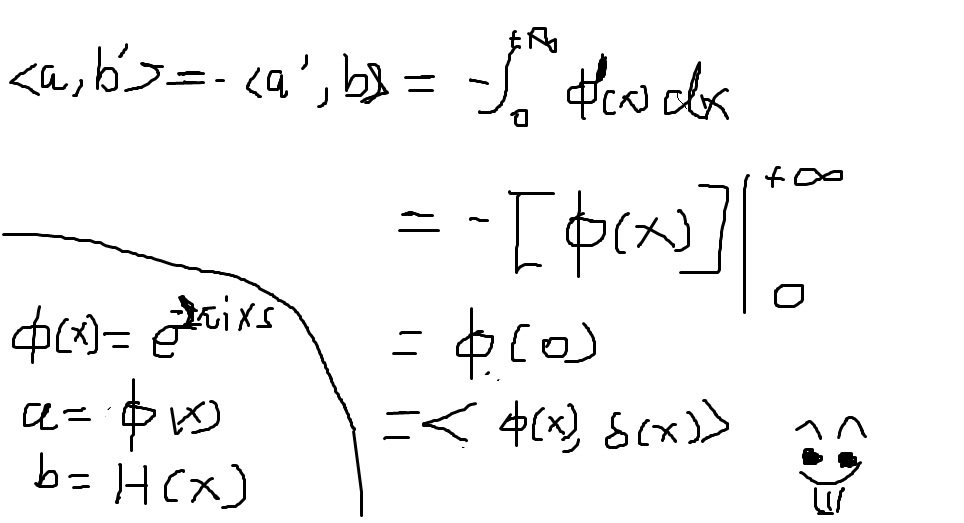阶跃函数的导数为什么是冲击函数 The derivative of heaviside step function is delta function

本文主要是介绍阶跃函数的导数为什么是冲击函数 The derivative of heaviside step function is delta function，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

如果我今天没搞懂这个，我估计我会抑郁到不能睡觉。

heaviside step function 就是所谓的阶跃函数：

定义

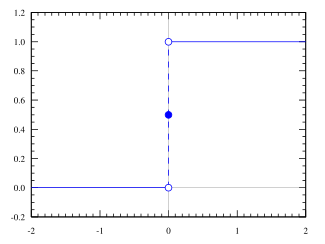
图像：

dirac delta function 狄利克雷函数，通常所说的冲击函数：

定义：

函数图像：

提出问题:

为什么heaviside step 函数的导数就是 dirac delta 函数呢？

感觉上是挺“靠谱”。阶跃函数嘛，在0点左右两侧导数都是0，然后0点导数无穷大，和delta函数对应得很好。

数学不是所谓“靠谱”就能搞定的。要证明，当然。。。我个数学渣渣，证明完全不行，而且各种大牛都已经证明过了。

只是。。。证明过的我都差点没看懂。于是，留下这篇blog，叨叨这个“为什么”，以及这个证明过程中，

我遇到的困惑，和怎么解决的。

看看这段话吧，

If  D  is a distribution, we want to define another distribution  D′ , its distributional derivative. This done by declaring  D′  by  (D′)(f)=−D(f′) ; 

more generally, the  n -th distributional derivative  D(n)  of  D  is defined by  (D(n))(f)=(−1)n(f(n)) . This is ok, since we assumed the test functions  f  

to be infinitely differentiable; it follows that distributions are infinitely differentiable (in another, in this sense). Notice the minus sign. This is because 

we want distributional derivatives to extend the ordinary derivative, notice that if  d  is differentiable,  ∫Rd′(x)f(x)dx=−∫Rd(x)f′(x)dx  since the

 boundary term vanishes by the decay condition imposed on the test functions  f .

看懂了也就知道为什么了，如果没看懂，那这篇blog还可以继续看下去。。。

我遇到的问题就是为什么

会有如此“操蛋”的事情捏。。。。。完全不符合分布积分的公式哇。。。(v*u)' = v'*u + v*u'

之后是各种苦恼。

Nothing to it.

注意这里是用了分布积分公式的！只是有一项被略去了，因为等于0！

H(x)是阶跃函数，那个希腊字母(x)是速降函数(不知道什么叫速降函数，其实就是指数函数，系数是负数)

这两个函数的乘积在正负无穷远处的值都是0，于是正无穷处的值减去负无穷处的值，0 - 0 = 0

于是就有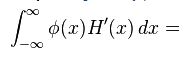  0    

理所当然的就有了上面的积分等式

我们用一种简单的标记方式来表示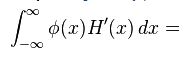 ---->      <a , b'>

于是

∫ Rd′(x)f(x)dx=−∫Rd(x)f′(x)

b的导数就是狄利克雷函数，有木有！b是什么，阶跃函数!

阶跃函数的导数就是狄利克雷函数，证明完毕！

开心，睡觉

The . L

 于 XTU  2014.03.13 凌晨

这篇关于阶跃函数的导数为什么是冲击函数 The derivative of heaviside step function is delta function的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---