本文主要是介绍数学知识(四)(容斥原理、博弈论),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、容斥原理
容斥原理公式
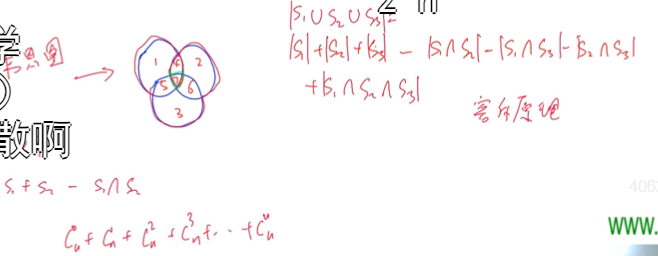
一共加或者减的式子个数
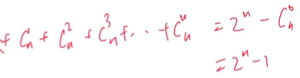
![]()
(一)利用容斥原理解决求能被质数整除的数的个数
890计算能被整除的数的个数
因为一共有2^n-1种选法,可以用位运算的方式枚举,对于得到的每一种选法,根据存在的数的个数判断前面是1还是-1。枚举到2^n-1的所有二进制数,判断每一位上的数是否是1,
最重要的转变是:将能被各个质数整除的集合看成一个个的集合。根据容斥原理,需要计算各个集合的组合方式的元素个数然后相加。在找组合方式的时候因为一共有2^n-1种,可以用m位的二进制数表示。如何计算一个一个组合的可以整除的个数。一位一位右移&1判断。
#include<bits/stdc++.h>
//890 求能被质数整除的数
using namespace std;
typedef long long LL;
const int N=20;
int n,m;
int p[N];
int main()
{cin>>n>>m;//读入所有的质数for(int i=0;i<m;i++)cin>>p[i];int res=0;//遍历所有二进制数for(int i=1;i<1<<m;i++){int cnt=0;int t=1;//遍历这个二进制数的所有位for(int j=0;j<m;j++){if(i>>j&1){//记录当前选择集合的个数cnt++;//并将集合元素相乘t*=p[j];//如果n一倍的t都装不了就breakif(t>n){t=-1;break;}}}if(t!=-1){if(cnt%2)res+=n/t;else res-=n/t;}}cout<<res<<endl;}
二、博弈论
891 先手是否先获胜
![]()
结论:

如果异或值不是0,先手可以拿一堆石子儿让拿之后状态变成必输。
异或不会产生1,只会消除1。

因为异或上x之后会ai一定会变小,也就是这一堆石子儿是可以让棋手拿的。最后剩余ai异或x。整个式子异或之后是0.也就是可以进行一次操作并得到一个对手必败的局面(不管对手怎么去拿异或之后都不为0)。也就是先手先胜利。
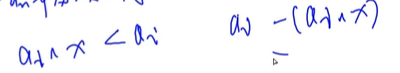
先手遇到的总不是0,后手遇到的总是0,最后后手败。
#include<bits/stdc++.h>
//891 Nim游戏
using namespace std;
typedef long long LL;
int main()
{int n;cin>>n;int res=0;while(n--){int x;cin>>x;res^=x;}if(res)puts("Yes");else puts("No");return 0;
}
三、sg函数
mex是某个点的出边指向的所有点的值(不再其中)的最小的自然数。

如果sg不为0,就说明有出边指向0
nim游戏和sg函数含义相似。每个结点的sg函数可以看做一个小石头堆。nim游戏中异或之后如果不等于0,可以找到ai,拿走ai-ai^x。最后得到的状态就是0。在sg中。如果异或之后的值非0,和nim一样,将其变成ai^x。因为 ai^x<ai.所以一定有一个出边指向ai^x成立,并且之后的状态变成0.
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_set>
using namespace std;
const int N = 110, M = 10010;
int n, m;
int s[N], f[M];
int sg(int x)
{if (f[x] != -1) return f[x];unordered_set<int> S;for (int i = 0; i < m; i ++ ){int sum = s[i];if (x >= sum) S.insert(sg(x - sum));}for (int i = 0; ; i ++ )if (!S.count(i))return f[x] = i;
}int main()
{cin >> m;for (int i = 0; i < m; i ++ ) cin >> s[i];cin >> n;memset(f, -1, sizeof f);int res = 0;for (int i = 0; i < n; i ++ ){int x;cin >> x;res ^= sg(x);}if (res) puts("Yes");else puts("No");return 0;
}这篇关于数学知识(四)(容斥原理、博弈论)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





