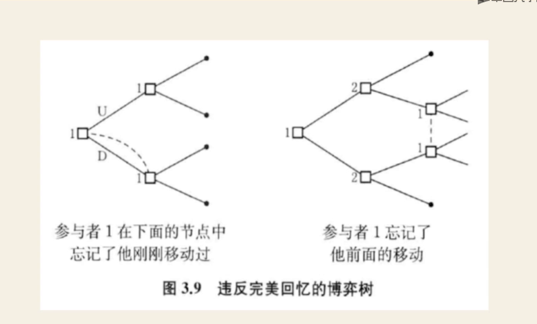
博弈论专题
【每日一题】【博弈论】【思维】会赢的! 牛客周赛 Round 58 C题 C++
牛客周赛 Round 58 C题 会赢的! 题目背景 牛客周赛 Round 58 题目描述 样例 #1 样例输入 #1 31 11 0-1 -1 样例输出 #1 NOYESPING 做题思路 首先考虑到开始位置为 ( 0 , 0 ) (0,0) (0,0)并且只能使横纵坐标递增。所以如果终点的横纵坐标为负数的情况是不可能到达的。所以平局。 第一个点: x
耶鲁大学《博弈论》公开课笔记
关于本文 该文章基于本人于当天白天看完耶鲁大学《博弈论》公开课后,于当晚记录下依然记得的白天所听内容。该文章为汇总,时间为记录一年后。 目录 关于本文2023.3.18 P103.19 P113.20 P123.21 P133.22 P143.23 P153.24 P163.25 P173.26 P183.27 P193.28 P203.29 P213.30 P223.31 P234.1
有向图游戏 SG函数【博弈论】C++
SG函数可以用来判断在一个给定的有向图游戏中,当前局面的胜负状态。 SG函数的定义如下: 设当前节点为v,那么SG(v)为当前局面的SG值。SG(v)的定义如下: - 如果当前节点v没有后继节点,则SG(v) = 0 - 如果当前节点v有若干个后继节点,分别为v1,v2,...,v_n,那么SG(v)为所有后继节点的SG值的异或和。即:SG(v) = SG(v1) XOR SG(v2) XOR
hdu 1524 A Chess Game 博弈论
题意: 两个人在一个有向五环图上面走棋子,每次只能走一步,最后谁 * 没有棋子可走就败,然后棋子可以重叠,并且有n个棋子。要求判断 * 先手的胜负。 纠结了好长时间一直在想为什么sg函数要呢么定义然后看了各种博客但是只是讲了,定义的内容却很少有讲为什么的。。。。 Description Let's design a new chess game. There are N
hdu4111 Alice and Bob 博弈论
题意:有N堆石子,每堆石子有一个数目,现有两个人博弈,每个人每次可以进行两个操作中的一个: 1、从某堆拿掉一个石子(若某堆石子为0了,那么这堆就不存在了);2、合并两堆石子 没有操作的就输。问是哪个赢 统计1的个数c,以及非1情况下的步数s,包括合并。 c为奇数,s不等于2:那么先手必胜。 s为2或者为0:c为3的倍数是先手必败。 否则的话,s为奇数时先手必胜。 首先没有1的情况下很好证明,就是
博弈论--巴什博弈——HDU1846
/*巴什博弈:HDU--1846*/ # include<iostream> using namespace std; int main() { int t; int n,m; cin>>t; while(t--) { cin>>n>>m; if(n%(m+1)==0) cout<<"sec
Codeforces Round 916 (Div. 3) E1. Game with Marbles(博弈论*1400)
感觉很难想。 如果你直接想的话,你就会发现有很多做法可以选择,而你根本不知道应该选哪个。 这时候可以先假设鲍勃已经取走了爱丽丝的所有的颜色的弹珠,(并且以每个颜色一个弹珠的代价)。 这时候每一项得分就是 S i = − ( b i − 1 ) S_i = -(b_i - 1) Si=−(bi−1)。 然后我们使得这时候爱丽丝的操作为取回弹珠,即她可以选择一种颜色的弹珠,并且直接取回,鲍勃
Codeforces Round 926 (Div. 2) C. Sasha and the Casino (博弈论*1400)
这里的意思是想让我们求得是否是能够实现不停地无上限的赚钱。 这里注意避开一个思维误区,如果你想的是前x次一直用1枚硬币然后吃第x+1次保底,那么就是错误的。你应该考虑到如果前x次里面出现了胜利呢?这时候你拿着一枚硬币根本赚不回本。 所以我们要假定:前x+1次,每一次都有可能胜利,并且每次胜利我们都需要使得自己能够赚回本金并且获得利润。 那么我们要怎么做才能够实现? 这里假设我们第i次投入
博弈论详解 1(基本理论定义 和 Nim 游戏)
公平博弈游戏 一般是两个玩家,轮流操作。是否能够必胜只和当前局面相关,不与现在是轮到哪个玩家相关(说白了就是不分黑白棋子,格点也不分黑白,都一样)。固定了开始状态后,可能的局面数是有限的。游戏一定会在有限步内结束 怎么才能赢? 必胜局面与必败局面 我们定义当前的局面对于先手(指的是要对当前局面进行操作的人,下面对先手的定义也相同)是必胜的为 N N N 局面,必败为 P P P 局面。
hdu2149 -- Public Sale(博弈论)
Public Sale Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 4594 Accepted Submission(s): 2778 Problem Description 虽然不想,但是现实总归是现实,L
hdu2147 -- kiki's game(博弈论)
因为每个坐标格的必胜或必败已经确定,只要画出P/N图就可以找出规律,获得代码: 博弈论:组合博弈 * 必败点(P点) :前一个选手(Previous player)将取胜的位置称为必败点。 * 必胜点(N点) :下一个选手(Next player)将取胜的位置称为必胜点。 * 必败(必胜)点的属性: * (1) 所有终结点是必败点(P点); * (2) 从任何必胜点(N点)操作,至少有
POJ1067 取石子游戏(博弈论)
取石子游戏 Time Limit: 1000MS Memory Limit: 10000KTotal Submissions: 36633 Accepted: 12396 Description 有两堆石子,数量任意,可以不同。游戏开始由两个人轮流取石子。游戏规定,每次有两种不同的取法,一是可以在任意的一堆中取走任意多的石子;二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者
博弈论(Nim 游戏)
公平组合游戏ICG 若—个游戏满足: 由两名玩家交替行动;在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关;不能行动的玩家判负; 则称该游戏为一个公平组合游戏。 NIM博弈属于公平组合游戏,但城建的棋类游戏,比如围棋,就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子,胜负判定也比较复杂,不满足条件 2 2 2 和条件 3 3 3。 可以看出,公平组合游戏不存在平局,而且
博弈论+递推+调和级数枚举,CF 1033C - Permutation Game
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 1033C - Permutation Game 二、解题报告 1、思路分析 我们考虑一个位置符合什么条件可以必胜? 如果可以跳到一个必败的位置 考虑最大的格子一定是必败 而每个格子只能跳到比自己大的格子 于是我们就可以倒序处理状态 对于每个格子枚举比自己大
专业学习|博弈论-博弈论概述
(一)认识博弈论:解析复杂决策与策略 (1)认识博弈 博弈论广泛应用于分析个体间因利益冲突而产生的决策问题。通过构建不同模型来探讨如经贸关系、军事威胁等问题,旨在寻找均衡解并提供新知,相较于计量经济学方法更为困难。政策制定与个体响应构成典型的博弈问题,反映上层政策与下层对策间的动态互动。 采用博弈建模是希望首先这个模型是可驾驭的,即一定是能够分析出均衡均衡
【读书笔记】《博弈论》ing
《博弈论》 朱富强著 June 7th ,2014 生活中的博弈论(game theory) 1.基于长远利益视域的理性理解 “一般的,人类与动物的重要区别就在于:人具有追求长期利益的理性,从而能约束自己的短视行为;相反,如果个体在采取行动时只是权衡一次性互动的功利量,那么也就等同动物的每一次斗争行为了。” 贪嘴一次,因猎奇心抽一次烟,偷吃一次禁果……这些按照现代主流经济
专业学习|博弈论-课程沿革
学习来源:北京大学刘霖《博弈论》MOOC公开课 备注:仅做学习分享,请勿转载,转载必究! (一)博弈论的预备知识 基本的微积分的知识和概率论的知识。简单的说会求导数,会求简单的积分,知道概率分布的含义、几种简单的概率分布,会求数学期望,了解贝叶斯法则。 博弈论本身的思维方式跟常规的思维方式不一样,要求你具有比较好的逻辑思维能力,以及基本的这个数学知识。内
耶鲁博弈论公开课笔记
这两周我看完了耶鲁大学的博弈论公开课,收获非常大,系统地了解了博弈论中的主要概念和方法,主要包括以下内容: 1. 首先是了解了很多的博弈模型,包括同步博弈中的古诺模型、伯川德模型、候选人-选民模型、谢林模型和序贯博弈中的最后通牒和讨价还价博弈、stackberg博弈、消耗战博弈以及不完整信息下的博弈、信息不对称博弈、重复博弈等众多博弈类型。我觉得最重要的是对问题进行抽象建立博弈模
策梅洛定理 (博弈论): Zermelo's theorem
很有意思的一个定理。 转载地址为http://blog.sina.com.cn/s/blog_4b91d3b501010hcj.html 策梅洛定理(英语:Zermelo's theorem)是博弈论的一条定理,以恩斯特·策梅洛命名。定理表示在二人的有限游戏中,如果双方皆拥有完全的资讯,并且运气因素并不牵涉在游戏中,那先行或后行者当中必有一方有必胜/必不败的策略。若应用至国际象棋,则策梅
acwing算法提高之数学知识--博弈论
目录 1 介绍2 训练 1 介绍 本博客用来记录博弈论相关的题目。 2 训练 题目1:1319移棋子游戏 C++代码如下, #include <cstdio>#include <cstring>#include <set>using namespace std;const int N = 2010, M = 6010;int n, m, k;int h[N], e[
ABS AtCoder - arc085_b(博弈论)
https://atcoder.jp/contests/arc085/tasks/arc085_b?lang=en 题意:1.初始状态,有N张牌,同时甲乙手中各一张牌,每张牌上有数字。 2.每个回合,先丢掉手中的牌,然后查看牌堆后选择N张牌中的任意前K张牌(1<=K<=N),同时只保留第K张牌,丢掉其他的牌。 3.甲先手 4.甲要让最终甲乙差的绝对值越大越好,乙要让最终甲乙差的绝对值越小越好。在
【AcWing】蓝桥杯集训每日一题Day22|区间DP|博弈论|1388.游戏(C++)
1388.游戏 1388. 游戏 - AcWing题库难度:中等时/空限制:1s / 64MB总通过数:1429总尝试数:1925来源:usaco training 3.3算法标签博弈论DP区间DP 题目内容 玩家一和玩家二共同玩一个小游戏。 给定一个包含 N 个正整数的序列。 由玩家一开始,双方交替行动。 每次行动可以在数列的两端之中任选一个数字将其取走,并给自己增加相应数字的分数。(
【博弈论1——认识博弈论】
1. 什么是博弈论 博弈论 是运筹学的一个分支,是一门以数学为基础,研究发生对抗与冲突时如何选择最优策略的学问。是交互式条件下“最优理性决策”精髓在于基于系统思维基础上的理性换位思考 重要的思维方式 2. 博弈的类型 按照是否有协议 合作博弈非合作博弈(经济学习中常指) 按照参与人是否得到全部信息 完全信息博弈不完全信息博弈 按参与者行动的先后顺序 静态博弈动态博弈 收益是否为常数 常