本文主要是介绍数学知识第九期 容斥原理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
容斥原理在数学上经常会被提及,是一种很重要的数学知识。
一、容斥原理的基本内容
简介:
在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
定义:
如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和= A类元素个数+ B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。(A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C) [2]。
例如:一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?
分析:依题意,被计数的事物有语、数得满分两类,“数学得满分”称为“A类元素”,“语文得满分”称为“B类元素”,“语、数都是满分”称为“既是A类又是B类的元素”,“至少有一门得满分的同学”称为“A类和B类元素个数”的总和。为15+12-4=23。
公式:
详细推理如下:
1、 等式右边改造 = {[(A+B - A∩B)+C - B∩C] - C∩A }+ A∩B∩C
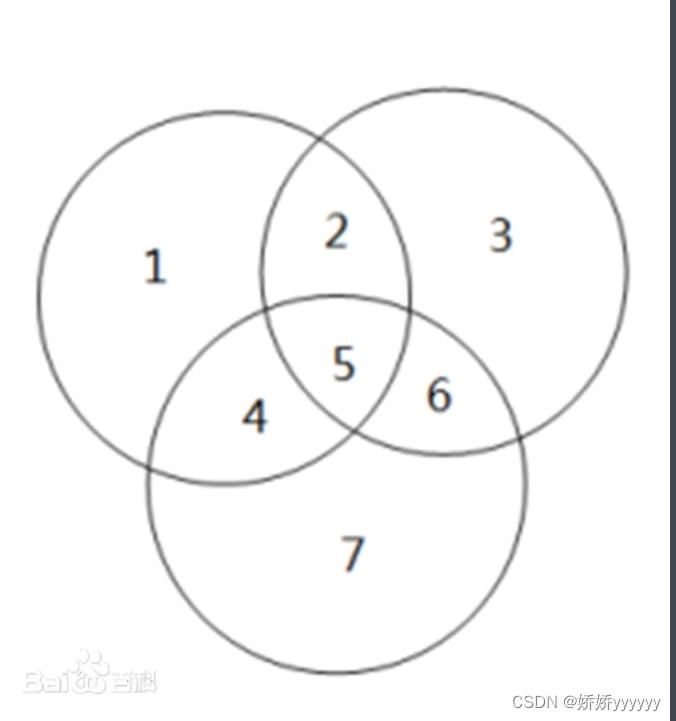
2、维恩图分块标记如右图图1:1245构成A,2356构成B,4567构成C
3、等式右边()里指的是下图的1+2+3+4+5+6六部分:
那么A∪B∪C还缺部分7。
4、等式右边[]号里+C(4+5+6+7)后,相当于A∪B∪C多加了4+5+6三部分,
减去B∩C(即5+6两部分)后,还多加了部分4。
5、等式右边{}里减去C∩A (即4+5两部分)后,A∪B∪C又多减了部分5,
则加上A∩B∩C(即5)刚好是A∪B∪C。
图片:
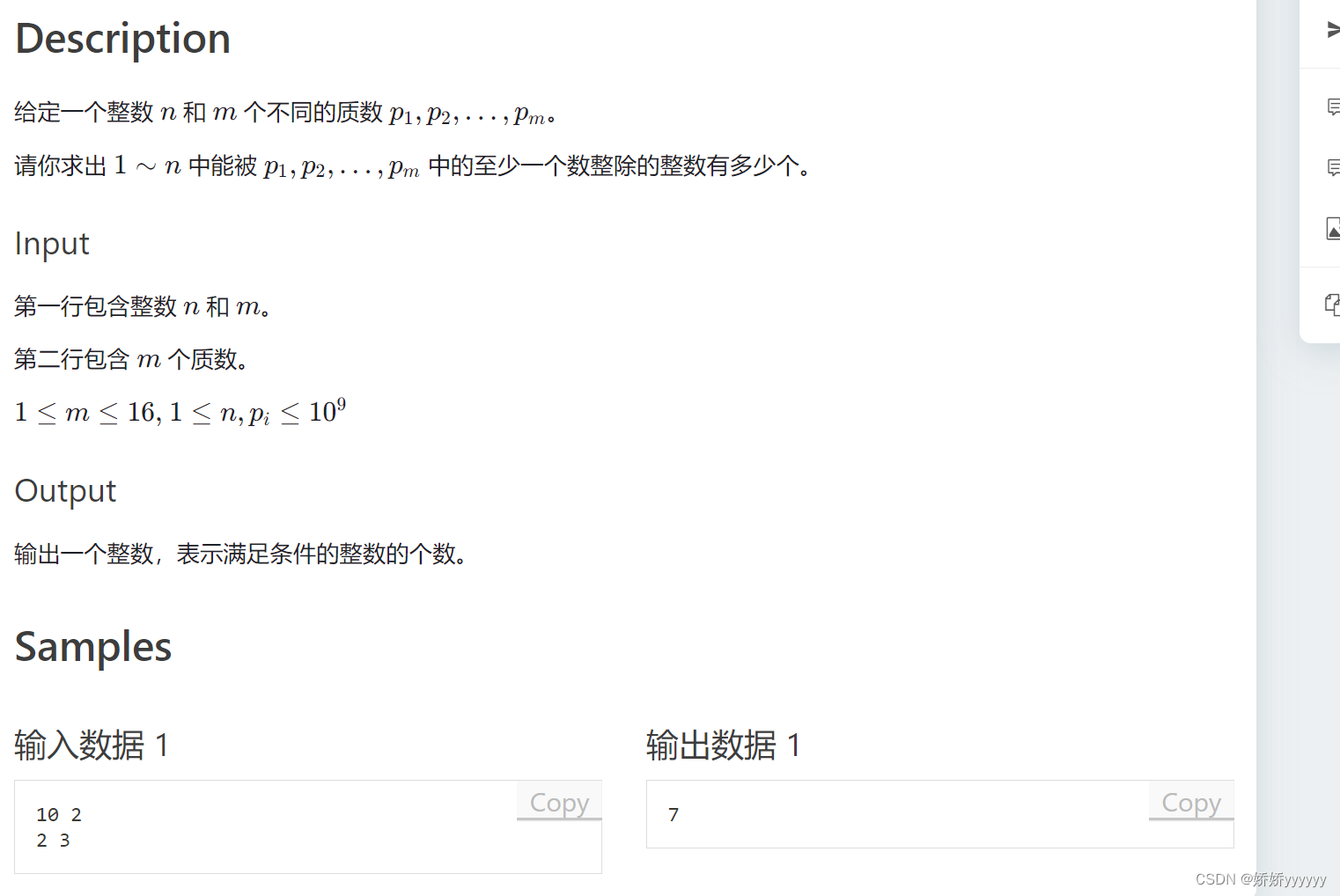
二、例题
AC代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
using LL = long long ;
int p[N], n, m;int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++ ) scanf("%d", &p[i]);int ans = 0;for (int i = 1; i < 1 << m; i ++ ) {int t = 1, cnt = 0;for (int j = 0; j < m; j ++ ) {if (i >> j & 1) {if ((LL)t * p[j] > n) {t = -1;break;}cnt ++ ;t *= p[j];}}if (t == -1) continue;cnt & 1 ? ans += n / t : ans -= n / t;}printf("%d\n", ans);return 0;
}
总结
·感谢大家的观看!!!
这篇关于数学知识第九期 容斥原理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!