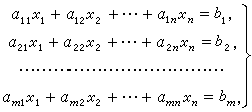acwing专题

【AcWing】851. 求最短路

spfa算法其实是对贝尔曼福特算法做一个优化。贝尔曼福特算法会遍历所有边来更新，但是每一次迭代的话我不一定每条边都会更新，SPFA是对这个做优化。如果说dist[b]在当前这次迭代想变小的话，那么一定是dist[a]变小了，只有a变小了，a的后继(b)才会变小。用宽搜来做优化，用一个队列，队列里边存的就是所有变小了的结点(队列里存的是待更新的点)。基本思路就是我更新过谁，我再拿

【AcWing】852. spfa判断负环

#include<iostream>#include<algorithm>#include<cstring>#include<queue>using namespace std;const int N= 1e5+10;int n,m;int h[N],w[N],e[N],ne[N],idx;int dist[N],cnt[N];//cnt存最短路径的边数bool st[N];v

AcWing 282. 石子合并

必看的视频讲解↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 【E28【模板】区间DP 石子合并——信息学竞赛算法】合并过程总开销等于红色数字总和，可以理解为花费的总体力！ f数组的含义是f【i】【j】是从第i堆石子开始到第j堆石子的花费体力最小值如何理解三层for呢？第一层for是控制区间长度len，第二层for是控制区间起点位置i，第三层for是控制区间

AcWing 897. 最长公共子序列

动态规划就是多见识应用题就完事儿了，也没有什么好说的。讲解参考：【E05 线性DP 最长公共子序列】 #include<iostream>#include<algorithm>#define N 1010using namespace std;char a[N],b[N];int n,m;int f[N][N];int main(){cin >> n >> m >> a

AcWing 2. 01背包问题

一定要看的视频讲解：↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 【E08【模板】背包DP 01背包——信息学竞赛算法】 i表示放入i个物品，j表示第j个物品，用于访问体积v【j】 #include <iostream>#include <algorithm>using namespace std;const int N = 1010;int n, m;int v[N]

AcWing-算法提高课（第一章）-下

区间DP 环形石子合并状态表示：f[i,j]（f[i,j]表示，在，由，将第i堆石子到第j堆石子合并成一堆石子的每个合并方式的代价，组成的集合，中，的最小值）状态计算：f[i,j]=min(f[i,k]+f[k+1,j]+s[j]-s[i-1])（s[j]表示第1堆石子到第j堆石子的总重量，s[i-1]表示第1堆石子到第i-1堆石子的总重量，s[j]-s[i-1]表示第i堆石子到第j堆石子的

贪心推公式——AcWing 125. 耍杂技的牛

贪心推公式定义贪心算法是一种在每一步选择中都采取在当前状态下最优的选择，希望通过局部的最优选择来得到全局最优解的算法策略。运用情况问题具有最优子结构，即一个问题的最优解包含其子问题的最优解。可以通过局部最优决策逐步推导到全局最优。问题的选择策略相对明确且易于计算。注意事项贪心算法并不总是能得到全局最优解，可能会陷入局部最优。对于一些复杂问题，需要谨慎验证其正确性。可能需要对

状态压缩DP——AcWing 291. 蒙德里安的梦想

状态压缩DP 定义状态压缩DP是一种利用二进制数来表示状态的动态规划算法。它通过将状态压缩成一个整数，从而减少状态数量，提高算法效率。运用情况状态压缩DP通常用于解决具有状态转移和最优解性质的问题，例如组合优化、图论、游戏等问题。它的基本思想是将问题的状态表示为一个二进制数，其中每一位表示一个元素或一个状态。通过对二进制数的位运算，可以方便地进行状态转移和最优解的计算。注意事项

AcWing算法基础课笔记——高斯消元

高斯消元用来求解方程组 a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 … a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n = b_1\\ a_

AcWing 1801：蹄子剪刀布 ← 模拟题

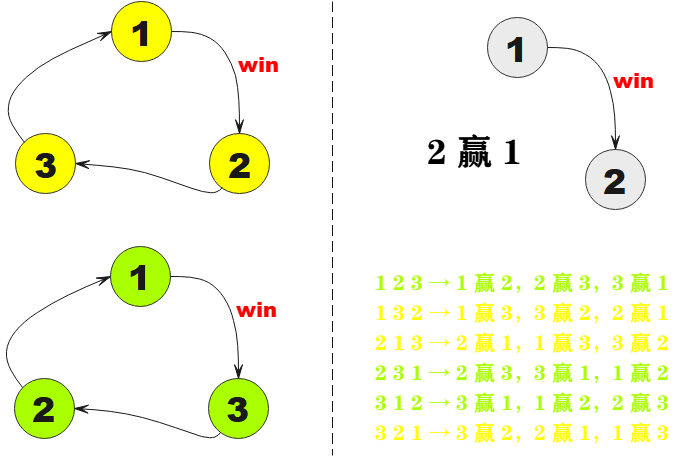
【题目来源】https://www.acwing.com/problem/content/1803/【题目描述】你可能听说过“石头剪刀布”的游戏。这个游戏在牛当中同样流行，它们称之为“蹄子剪刀布”。游戏的规则非常简单，两头牛相互对抗，数到三之后各出一个表示蹄子，剪刀或布的手势。蹄子赢剪刀，剪刀赢布，布赢蹄子。例如，第一头牛出“蹄子”手势，第二头牛出“布”手势，则第二头牛获胜。如果两头牛出

数位统计DP——AcWing 338. 计数问题

数位统计DP 定义数位DP（Digital DP）是一种用于解决与数字的数位相关问题的动态规划算法。它将数字的每一位看作一个状态，通过转移状态来计算满足特定条件的数字个数或其他相关统计信息。运用情况统计满足特定条件的数字个数，例如在给定范围内有多少个数字满足某些数位特征。计算数字的某个数位上的特定统计信息，如出现的数字频率等。解决与数字排列、组合相关的问题。注意事项数位DP的

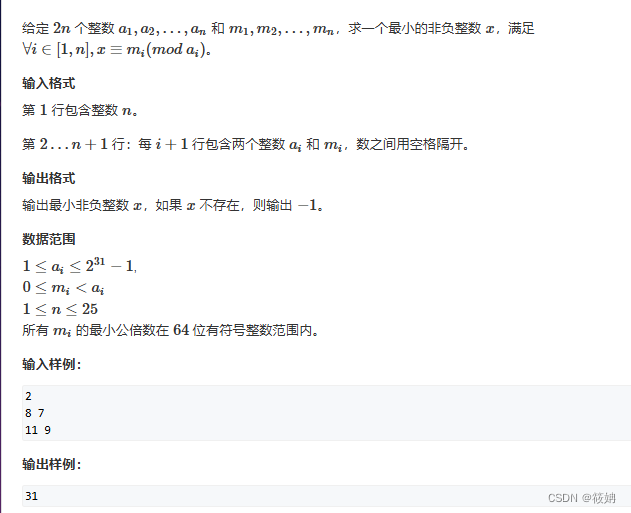
中国剩余定理——AcWing 204. 表达整数的奇怪方式

中国剩余定理定义中国剩余定理最早出自我国古代的《孙子算经》，是数论中的一个重要定理。它描述了这样一种情况：在模运算下，对于一组线性同余方程组，存在唯一解的条件和求解方法。运用情况常用于在一些涉及到按不同模的余数条件下求解问题。比如在密码学、计算数论、计算机科学等领域中，当需要处理多个模条件相关的计算时，常常会用到中国剩余定理。注意事项要求各个模之间互质，否则定理不直接适用，

计数类DP——AcWing 900. 整数划分

计数类DP 定义计数类DP主要是通过动态规划的方法来计算满足特定条件的方案数、组合数等数量相关的问题。运用情况需要计算不同排列、组合或情况的数量。问题具有明显的阶段性，且每个阶段的选择会对后续阶段产生影响。可以通过逐步构建较小规模问题的解来推导出大规模问题的解。注意事项状态定义要准确合理，确保能够涵盖所有需要计数的情况。边界条件的处理要小心，避免出现错误。注意状态转移的正确性

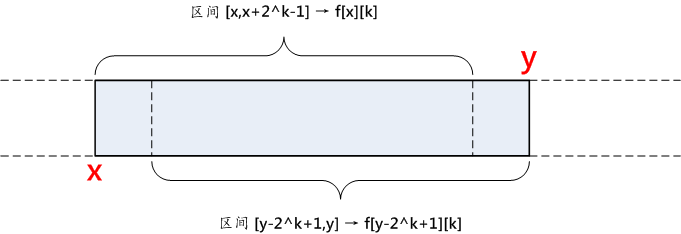
AcWing 1273：天才的记忆 ← ST算法求解RMQ问题

【题目来源】https://www.acwing.com/problem/content/1275/【题目描述】从前有个人名叫 WNB，他有着天才般的记忆力，他珍藏了许多许多的宝藏。在他离世之后留给后人一个难题（专门考验记忆力的啊！），如果谁能轻松回答出这个问题，便可以继承他的宝藏。题目是这样的：给你一大串数字（编号为 1 到 N，大小可不一定哦！），在你看过一遍之后，它便消失在你面前，随后

acwing 5575. 改变数值 | c++题解及解释

acwing 5575. 改变数值题目代码及解释 #include <iostream>#include <cstring>#include <algorithm>#include <unordered_map>using namespace std;const int N=305;int a[N],b[N];unordered_map<int,int>f[N];

AcWing 848：拓扑排序 ← 链式前向星存图

【题目来源】https://www.acwing.com/problem/content/850/【问题描述】给定一个 n 个点 m 条边的有向图，点的编号是 1 到 n，图中可能存在重边和自环。请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑

AcWing 33：链表中倒数第k个节点 ← 尾插法

【题目来源】https://www.acwing.com/problem/content/32/【题目描述】输入一个链表，输出该链表中倒数第 k 个结点。注意： ● k >= 1; ● 如果 k 大于链表长度，则返回 NULL；【数据范围】链表长度 [0,30]。【输入样例】输入：链表：1->2->3->4->5 ，k=2【输出样例】输出：4【算法分析】 ● 假设链表有

字典树，AcWing 5726. 连续子序列

一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 5726. 连续子序列 - AcWing题库二、解题报告 1、思路分析字典树存储前缀和考虑边遍历计算前缀和，边查询字典树查询流程：记当前前缀和为s 如果当前位k为1，那么s 必须走当前位和自己不同的结点如果当前位k为0，那么我们加上当前位和s不

AcWing 1600：完全二叉树

【题目来源】https://www.acwing.com/problem/content/1602/【题目描述】给定一个树，请你判断它是否是完全二叉树。【输入格式】第一行包含整数 N，表示树的结点个数。树的结点编号为 0∼N−1。接下来 N 行，每行对应一个结点，并给出该结点的左右子结点的编号，如果某个子结点不存在，则用 - 代替。【输出格式】如果是完全二叉树，则输出 YES 以及最后一

AcWing 143. 最大异或对——算法基础课题解

AcWing 143. 最大异或对题目描述在给定的 𝑁 个整数 𝐴1，𝐴2……𝐴𝑁 中选出两个进行 𝑥𝑜𝑟（异或）运算，得到的结果最大是多少？输入格式第一行输入一个整数 𝑁。第二行输入 𝑁 个整数 𝐴1～𝐴𝑁。输出格式输出一个整数表示答案。数据范围 1≤𝑁≤10^5, 0≤𝐴𝑖<2^31 输入样例： 31 2 3 输出样

贪心-AcWing 1522. 排成最小的数字-XMUOJ石板序列

题目思路 getline() 是 C++ 标准库中的一个函数，用于从输入流中读取一行文本，并将其存储为字符串。它可以从标准输入、文件流、字符串流等不同类型的输入流中读取数据。C++中istringstream、ostringstream、stringstream详细介绍和使用_c++ istringstream-CSDN博客话不多说，直接上代码代码 /*AcWing 1522. 排

树形DP-AcWing 285. 没有上司的舞会-XMUOJ提瓦特庆典策划

题目思路话不多说，直接上代码代码 /*AcWing 285. 没有上司的舞会-XMUOJ提瓦特庆典策划--JinlongW-2024/05/26 */#include <bits/stdc++.h>using namespace std;const int N=7000;int st[N];//标记是否有父亲结点int happy[N];int d

AcWing 831. KMP字符串——算法基础课题解

AcWing 831. KMP 字符串题目描述给定一个字符串 𝑆，以及一个模式串 𝑃，所有字符串中只包含大小写英文字母以及阿拉伯数字。模式串 𝑃 在字符串 𝑆 中多次作为子串出现。求出模式串 𝑃 在字符串 𝑆 中所有出现的位置的起始下标。输入格式第一行输入整数 𝑁，表示字符串 𝑃 的长度。第二行输入字符串 𝑃。第三行输入整数 𝑀，表示字符串 𝑆

AcWing 154. 滑动窗口——算法基础课题解

AcWing 154. 滑动窗口题目描述给定一个大小为 n≤10^6 的数组。有一个大小为 𝑘 的滑动窗口，它从数组的最左边移动到最右边。你只能在窗口中看到 𝑘 个数字。每次滑动窗口向右移动一个位置。以下是一个例子：该数组为 [1 3 -1 -3 5 3 6 7]，𝑘 为 3。窗口位置最小值最大值[1 3 -1] -3 5 3 6 7-131 [3 -1 -3

AcWing 3302. 表达式求值——算法基础课题解

AcWing 3302. 表达式求值题目描述给定一个表达式，其中运算符仅包含 +,-,*,/（加减乘整除），可能包含括号，请你求出表达式的最终值。注意：数据保证给定的表达式合法。题目保证符号 - 只作为减号出现，不会作为负号出现，例如，-1+2,(2+2)*(-(1+1)+2) 之类表达式均不会出现。题目保证表达式中所有数字均为正整数。题目保证表达式在中间计算过程以及结果中，

AcWing 1644. 二叉树中的最低公共祖先题解线性dp 倍增算法前序中序构造二叉树

二叉树中的最低公共祖先题目描述树中两个结点 U 和 V 的最低公共祖先（LCA）是指同时具有 U 和 V 作为后代的最深结点。给定二叉树中的任何两个结点，请你找到它们的 LCA。输入描述第一行包含两个整数 M 和 N ，分别表示询问结点对数以及二叉树中的结点数量。接下来两行，每行包含 N 个不同的整数，分别表示二叉树的中序和前序遍历。保证二叉树可由给定遍历序列唯一确定。接下来