本文主要是介绍高斯消元练习,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
POJ 1222 EXTENDED LIGHTS OUT
http://poj.org/problem?id=1222
开关灯问题:每一个开关对四周5点领域都有影响,状态变化:如果灯是亮着的,熄灭;如果灯是熄灭的,亮起。把每一个开关的开闭看做一个未知数x,影响领域看做系数a,每一盏灯现在的状态是y,问题就是  . 等式解释:如果灯是关着的,那么
. 等式解释:如果灯是关着的,那么  必须等于0,维持状态;如果灯是开着的,
必须等于0,维持状态;如果灯是开着的,  必须等于1,改变状态。
必须等于1,改变状态。
对于“ 5点领域”换个角度看,只有周围的5盏灯会对其产生影响,所以他们的当前系数是1。有:

POJ 1830 开关问题
假设有规模为3*3的9盏灯:
0 1 0
1 0 0
1 1 1
增广矩阵对应的是:
1 1 0 1 0 0 0 0 0 0
1 1 1 0 1 0 0 0 0 1
0 1 1 0 0 1 0 0 0 0
1 0 0 1 1 0 1 0 0 1
0 1 0 1 1 1 0 1 0 0
0 0 1 0 1 1 0 0 1 0
0 0 0 1 0 0 1 1 0 1
0 0 0 0 1 0 1 1 1 1
0 0 0 0 0 1 0 1 1 1
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=905;
int gcd(int a,int b){return b==0?a:gcd(b,a%b);
}
// a[][]:增广矩阵 n: 方程数 m:变量数
void Gauss(int a[N][N],int n,int m,int &r,int &c){for(r=0,c=0;r<n&&c<m;r++,c++){int maxi=r;for(int i=r+1;i<n;i++){if(abs(a[i][c])>abs(a[maxi][c])) maxi=i;}if(maxi!=r){for(int j=r;j<m+1;j++){ swap(a[r][j],a[maxi][j]);}}if(a[r][c]==0){r--;continue;}for(int i=r+1;i<n;i++){if(a[i][c]!=0){int x=abs(a[i][c]);int y=abs(a[r][c]);int lcm=x/gcd(x,y)*y;int tx=lcm/x;int ty=lcm/y;if(a[i][c]*a[r][c]<0) ty=-ty;for(int j=c;j<m+1;j++){a[i][j]=(a[i][j]*tx-a[r][j]*ty+2)%2;}}}}
}
int reback(int a[][N],int n,int m,int r,int c,int x[]){for(int i=r-1;i>=0;i--){int t=a[i][c];for(int j=i+1;j<c;j++) t-=a[i][j]*x[j];x[i]=t/a[i][i]%2;x[i]=(x[i]+2)%2;}return 0;
}int a[N][N];
int x[N];int main(){int t;int ca=1;scanf("%d",&t);while(t--){memset(a,0,sizeof(a));for(int i=0;i<5;i++){for(int j=0;j<6;j++){a[6*i+j][6*i+j]=1;if(i>0) a[6*i+j][6*(i-1)+j]=1;if(i<4) a[6*i+j][6*(i+1)+j]=1;if(j>0) a[6*i+j][6*i+j-1]=1;if(j<5) a[6*i+j][6*i+j+1]=1;}}for(int i=0;i<5;i++){for(int j=0;j<6;j++) scanf("%d",&a[6*i+j][30]);}int r,c;Gauss(a,30,30,r,c);reback(a,30,30,r,c,x);printf("PUZZLE #%d\n",ca++);for(int i=0;i<30;i++){if((i+1)%6==0) printf("%d\n",x[i]);else printf("%d ",x[i]);}}return 0;
}POJ 1830 开关问题
http://poj.org/problem?id=1830
大意:给出所有灯的开始和结束状态,开关之间的影响关系,求出有多少种方案能使得状态改变成功
和上一题有点类似。用数学表达:

如果存在自由变元,答案则是2^ans
如果方案唯一,则是2^0。总之就是1<<ans
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=30;
int gcd(int a,int b){return b==0?a:gcd(b,a%b);
}
void Gauss(int a[N][N],int n,int m,int &r,int &c){for(r=0,c=0;r<n&&c<m;r++,c++){int maxi=r;for(int i=r+1;i<n;i++){if(a[i][c]>a[maxi][c]) maxi=i;}if(maxi!=r){for(int j=r;j<m+1;j++){swap(a[r][j],a[maxi][j]);}}if(a[r][c]==0){r--;continue;}for(int i=r+1;i<n;i++){if(a[i][c]&&a[r][c]){for(int j=c;j<m+1;j++){a[i][j]=(a[i][j]-a[r][j]+2)%2;}}}}
}
// -2 没有整数解 -1:无解 0: 唯一解 m-r:(自由变元个数)无穷多个解
int reback(int a[][N],int n,int m,int r,int c,int x[],bool tag[]){for(int i=r;i<n;i++) if(a[i][c]!=0) return -1;if(r<m){memset(tag,0,sizeof(tag));for(int i=r-1;i>=0;i--){int dex=0;int cnt=0;for(int j=0;j<m;j++){if(a[i][j]!=0&&tag[j]==0){cnt++;dex=j;}}if(cnt>1) continue;int t=a[i][m];for(int j=0;j<m;j++){if(a[i][j]!=0&&j!=dex){t-=a[i][j]*x[j];}}x[dex]=t/a[i][dex]%2;x[dex]=(x[dex]+2)%2;tag[dex]=1;}return m-r;}for(int i=r-1;i>=0;i--){int t=a[i][c];for(int j=i+1;j<c;j++) t-=a[i][j]*x[j];if(t%a[i][i]!=0) return -2;x[i]=t/a[i][i]%2;x[i]=(x[i]+2)%2;}return 0;
}
int e1[N],e2[N];
int a[N][N];
int x[N];
bool tag[N];
int main()
{//freopen("cin.txt","r",stdin);int k;cin>>k;while(k--){memset(a,0,sizeof(a));int N;scanf("%d",&N);for(int i=0;i<N;i++) scanf("%d",&e1[i]);for(int i=0;i<N;i++) scanf("%d",&e2[i]);for(int i=0;i<N;i++) {a[i][N]=(e2[i]-e1[i]+2)%2;a[i][i]=1;}int p1,p2;while(scanf("%d%d",&p1,&p2)){if(p1+p2==0) break;a[p2-1][p1-1]=1;}int r,c;Gauss(a,N,N,r,c);int g=reback(a,N,N,r,c,x,tag);if(g<0) printf("Oh,it's impossible~!!\n");else printf("%d\n",1<<g);}return 0;
}POJ 2947 Widget Factory
http://poj.org/problem?id=2947
大意:周期性时间问题,建立模线性方程组。每一个装饰物的加工应该是需要一定人手的,且有一定的工作时间。设每一个装饰物的加工时间为 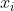 , 有
, 有 
例如例一:
#include <iostream>
#include <cstdio>
#include <map>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=305;int gcd(int a,int b){return b==0?a:gcd(b,a%b);
}void Gauss(int a[N][N],int n,int m,int &r,int &c){for(r=0,c=0;r<n&&c<m;r++,c++){int maxi = r;for(int i=r+1; i<n; i++)if(a[i][c] > a[maxi][c])maxi = i;if(maxi != r){for(int i=r; i<m+1; i++)swap(a[r][i],a[maxi][i]);}if(a[r][c] == 0){r--;continue;}for(int i=r+1; i<n; i++){if(a[i][c] != 0){int LCM = a[i][c]/gcd(a[i][c],a[r][c])*a[r][c];int tx = LCM / a[i][c];int ty = LCM / a[r][c];for(int j=c; j<m+1; j++)a[i][j] = ((a[i][j] % 7 * tx % 7 - a[r][j] % 7 * ty % 7) % 7 + 7) % 7;}}}
}
//-2 没有整数解 这一情况除去,模线性方程中没有整除的概念
// -1:无解 0: 唯一解 m-r:(自由变元个数)无穷多个解
int reback(int a[][N],int n,int m,int r,int c,int x[],bool tag[]){for(int i=r;i<n;i++) if(a[i][c]!=0) return -1;if(r<m) return m-r;for(int i=r-1;i>=0;i--){int t=a[i][c];for(int j=i+1;j<c;j++) {t-=a[i][j]*x[j]%7;t=(t%7+7)%7;}//if(t%a[i][i]!=0) return -2;//int ni,y;//exgcd(t,a[i][i],ni,y);//ni=(ni%7+7)%7;//x[i]=t*ni%7;while(t%a[i][i]!=0) t+=7;x[i]=t/a[i][i]%7;if(x[i]<3) x[i]+=7;}return 0;
}int a[N][N];
int x[N];
bool tag[N];
struct StrCmp{bool operator()(const char *s1,const char *s2)const{return strcmp(s1,s2)<0;}
};
map<const char *,int,StrCmp> mp;
int main()
{//freopen("cin.txt","r",stdin);mp["SUN"]=0;mp["MON"]=1;mp["TUE"]=2;mp["WED"]=3;mp["THU"]=4;mp["FRI"]=5;mp["SAT"]=6;int n,m;while(cin>>n>>m){if(n+m==0) break;memset(a,0,sizeof(a));int k,dex;char s1[10],s2[10];for(int i=0;i<m;i++){scanf("%d%s%s",&k,s1,s2);a[i][n]=((mp[s2]-mp[s1]+1)%7+7)%7; // fired day countsfor(int j=0;j<k;j++){scanf("%d",&dex);a[i][dex-1]=(a[i][dex-1]+1)%7;}}int r,c;Gauss(a,m,n,r,c);int g=reback(a,m,n,r,c,x,tag);if(g>0) printf("Multiple solutions.\n");else if(g<0) printf("Inconsistent data.\n");else {for(int i=0;i<n-1;i++) printf("%d ",x[i]);printf("%d\n",x[n-1]);}}return 0;
}这篇关于高斯消元练习的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





