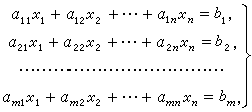AcWing.883.高斯消元解线性方程组

本文主要是介绍AcWing.883.高斯消元解线性方程组，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

输入一个包含 n 个方程 n 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 m 个方程 n 个未知数的线性方程组示例：
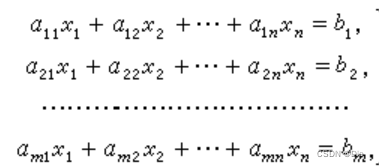
在这里插入图片描述
输入格式
第一行包含整数 $n$ 。

接下来 $n$ 行，每行包含 $n + 1$ 个实数，表示一个方程的 $n$ 个系数以及等号右侧的常数。

输出格式
如果给定线性方程组存在唯一解，则输出共 $n$ 行，其中第 $i$ 行输出第 $i$ 个未知数的解，结果保留两位小数。

注意：本题有 SPJ，当输出结果为 $0.00$ 时，输出 $- 0.00$ 也会判对。在数学中，一般没有正零或负零的概念，所以严格来说应当输出 $0.00$ ，但是考虑到本题作为一道模板题，考察点并不在于此，在此处卡住大多同学的代码没有太大意义，故增加 SPJ，对输出 $- 0.00$ 的代码也予以判对。

如果给定线性方程组存在无数解，则输出 Infinite group solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围
$1 \leq n \leq 100$ ,所有输入系数以及常数均保留两位小数，绝对值均不超过 $100$ 。

输入样例：

1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：

-2.00
3.00

通过高斯消元，来使方程变为上三角形式，从而可以解得方程（大学线性代数）
如果消过之后，是完美的上三角形，那么会得到唯一解
如果中间出现 $0 =$ （非零）的方程，那么无解
如果中间出现 $0 = 0$ 的方程，那么就有无穷多解

高斯消元的过程：
枚举每一列：
(1)每次枚举找到绝对值最大的一行
(2)将这一行换到最上面
(3)然后将这一行的第一个数变成1
(4)将下面所有行的当前列消成0。之后继续枚举，但是被换到最上面的那一行就不要动了，直至最后。

#include<iostream>
#include<cmath>
using namespace std;
const int N = 110;
const double eps = 1e-8;//浮点数存储有精度问题，小于一个很小的数就相当于等于0了int n;
double a[N][N];	//存系数矩阵int gauss() {int c, r;	//c：列，r：行for (c = 0, r = 0; c < n; c++) {	//枚举每一列int t = r;	//从这一行开始for (int i = r; i < n; i++)	//找到当前这一列绝对值最大的一行if (fabs(a[i][c]) > fabs(a[t][c]))//fabs()：浮点绝对值t = i;if (fabs(a[t][c]) < eps)  continue;	//如果行绝对值的最大值都是0，那么直接跳//因为后续的操作就是为了把其化为0，如果已经为0，那么就不需要进行下面的操作了for (int i = c; i <= n; i++)swap(a[t][i], a[r][i]);//把绝对值最大的这行换到最上面//要倒着进行，不然第一个数（第c列）变成1，后面除的数都不对了for (int i = n; i >= c; i--) a[r][i] /= a[r][c];//把这一行的第一个数变成1（整个方程都需要同步除）for (int i = r + 1; i < n; i++) {		//把下面所有行的第一个数消成0if (fabs(a[i][c]) > eps) {			//如果不是0再进行操作for (int j = n; j >= c; j--)a[i][j] -= a[r][j] * a[i][c];//把整个方程减去变成1的那个方程的倍数	}}r++;//可操作的行减少一个}if (r < n) {	//如果处理过的行小于所有的行，则进行进一步判断for (int i = r; i < n; i++) {	//如果没有等于0的行，即(0 = (非零))if (fabs(a[i][n]) > eps)return 2;//就是无解}return 1;	//如果有0 = 0 那么有无穷多解}for (int i = n - 1; i >= 0; i--)		//从下往上，一步步的把下面x的解往上面带for (int j = i + 1; j < n; j++)		//从而求解出所有的x的解a[i][n] -= a[i][j] * a[j][n];	//减的就是上几行的x的解，因为是上三角形状//减完之后等号右面的值就是这一行的x的解return 0;//唯一解
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;for (int i = 0; i < n; i++) {	//读入for (int j = 0; j < n + 1; j++) {	//因为还有得数，所以到n+1cin >> a[i][j];}}int t = gauss();//用0表示唯一解，1表示无穷解，2表示无解if (t == 0) {for (int i = 0; i < n; i++) printf("%.2lf\n", a[i][n]);//到最后，矩阵最右面的系数已经是各个x的值了}else if (t == 1) puts("Infinite group solutions");else puts("No solution");return 0;
}