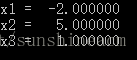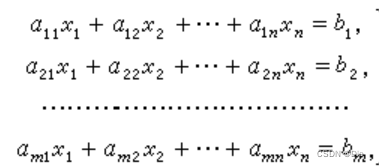线性方程组专题

线性代数第五讲:线性方程组_齐次线性方程组_非齐次线性方程组_公共解同解方程组_详解

线性方程组文章目录线性方程组1.齐次线性方程组的求解1.1 核心要义1.2 基础解系与线性无关的解向量的个数1.3 计算使用举例 2. 非齐次线性方程的求解2.1 非齐次线性方程解的判定2.2 非齐次线性方程解的结构2.3 计算使用举例 3.公共解与同解3.1 两个方程组的公共解3.2 同解方程组 4.重难点题型总结4.1 抽象齐次线性方程组的求解4.1 含有系数的非齐次线性方程组的求

通义说【线性代数】线性方程组和线性代数的关系

线性方程组和线性代数之间有非常紧密的关系。事实上，线性方程组是线性代数的一个核心主题，而线性代数提供了解决线性方程组的一系列理论和工具。线性方程组线性方程组是由一组线性方程构成的集合，每个方程都表示未知变量的线性组合等于一个常数项。一个典型的线性方程组可以写作： a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 +

DeepSORT（目标跟踪算法）中的解三角方程计算标准化残差（解线性方程组）

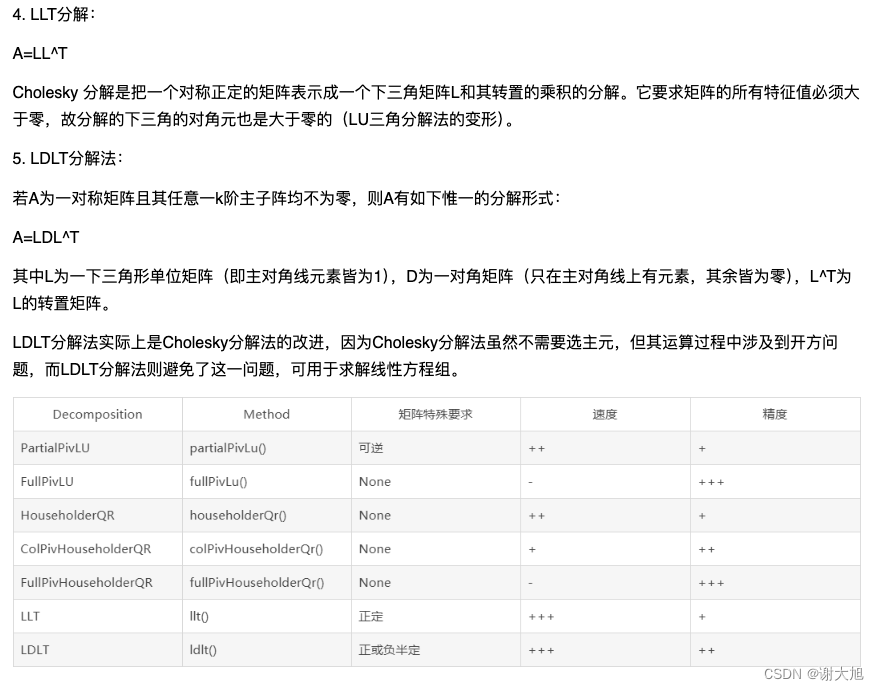
DeepSORT（目标跟踪算法）中的解三角方程计算标准化残差（解线性方程组） flyfish 《DeepSORT（目标跟踪算法）中的计算观测值与状态估计的马氏距离》这篇文章介绍了Cholesky 分解。Cholesky 分解将协方差矩阵分解成下三角矩阵，使得求解过程可以高效进行。这篇是利用 solve_triangular 函数，我们可以高效地解这些线性方程组，从而得到标准化残差和更新后的状态

matlab实现牛顿迭代法求解非线性方程组

已知非线性方程组如下 3*x1-cos(x2*x3)-1/2=0 x1^2-81*(x2+0.1)^2+sin(x3)+1.06=0 exp(-x1*x2)+20*x3+(10*pi-3)/3=0 求解要求精度达到0.00001 ---------------------------------------------------------分--割--线------------

【线性代数】第五章-线性方程组

文章目录一. 基本内容与重要结论1. 线性方程组的定义2. 线性方程组的初等变换3. 基础解系二. 主要定理1. 初等行变换可得同解方程组2. 解的情况3. 齐次有解的定理4. (齐次)基础解系的构成ing5. 非齐次有解定理6. 解的性质与结构本章需要掌握内容理解线性方程组解的概念.非齐次线性方程组Ax = b可能有解(唯一解或无穷多解)，亦可能无解，要理解方程组有解

【线性代数】第三章-矩阵的初等变换与线性方程组：以及秩、行阶梯的概念

文章目录一. 矩阵的初等变换1. 矩阵的三种初等变换2. 矩阵等价3. 初等矩阵二. 行阶梯矩阵1. 行阶梯矩阵定义2. 定理二. 矩阵的秩1. k阶子式的概念2. 秩的定义3. 秩的性质三. 线性方程组的解1. 线性方程组的向量形式2. 线性方程组解的讨论3. 定理一. 矩阵的初等变换 1. 矩阵的三种初等变换 2. 矩阵等价矩阵等价性质

Eigen求解线性方程组

1、线性方程组的应用线性方程组可以用来解决各种涉及线性关系的问题。以下是一些通常可以用线性方程组来解决的问题：在实际工程和科学计算中，求解多项式方程的根有着广泛的应用。在控制系统的设计中，我们经常需要求解特征方程的根来分析系统的稳定性; 在图像处理和模式识别中，多项式方程的根可以用来寻找图像的特征点; 在金融工程和风险管理中，多项式方程的根可以用来对数据进行拟合和预测。工程问

【智能算法应用】麻雀搜索算法求解非线性方程组问题

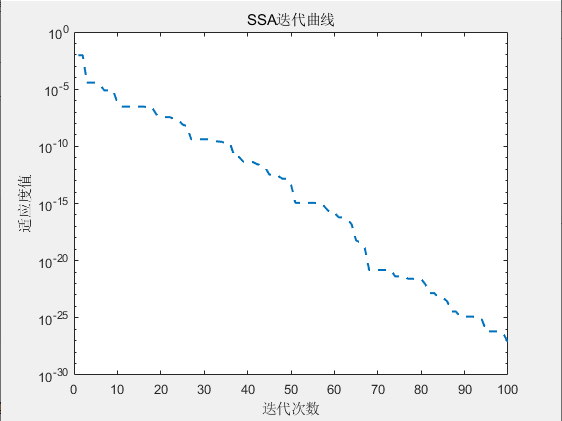
目录 1.算法原理2.数学模型3.结果展示4.代码获取 1.算法原理【智能算法】麻雀搜索算法（SSA）原理及实现 2.数学模型非线性方程组为： 2 x 1 − x 2 = e − x 1 − x 1 + 2 x 2 = e − x 2 (1) \begin{aligned}&2x_1-x_2=e^{-x_1}\\&-x_1+2x_2=e^{-x_2}\end{al

POJ 2891 模线性方程组（mi mj 不互素)

题解： x = ai ( mod mi ) 1 <= i <= k 先考虑k==2的情况： x = a1 ( mod m1 ) x = a2 ( mod m2 ) 方程组有解的充分必要条件是： d | (a1-a2) ，其中 d = (m1,m2) 证明如下：必要性：设 x 是上面同余方程组的解，从而存在整数q1,q2使得x=a1+m1*q1，x=a2+m2*q2，消去x即得a

解线性方程组——直接解法：LU分解、PLU分解(类似列主元消去法) | 北太天元

L: lower triangular 下三角 U: upper triangular 上三角 LU 分解，顾名思义，为把一个矩阵分成一个下三角矩阵乘上一个上三角矩阵的形式。 Example 为什么可以这样几个基本的初等行变换，可以自己验算一下，等式的左边与右边是相等的用上面这几个等式，重新看一下第一个例子，对A进行了三次行变换，得到上三角矩阵U，两边同时左乘初等

线性代数实验(二)线性方程组，特征值与特征向量

一、线性方程组 Matlab求解线性方程组的命令格式： rank(A)：求矩阵A的秩； rref(A)：求矩阵A的行最简形； null(A)：求系数矩阵为A的齐次方程组的基础解系； Null(A,’r’)：求系数矩阵为A的齐次方程组有理数形式的基础解系； XA=B： x=B/A, 求矩阵方程唯一解或最小范数解；三、特征值与特征向量 Matlab命令格式： trace(A)：返回矩阵A的迹. po

0201线性方程组和矩阵-矩阵及其运算-线性代数

文章目录一、线性方程组二、矩阵的定义结语一、线性方程组设有 n 个未知数 m n个未知数m n个未知数m个方程的线性方程组 { a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 , a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 , ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m

【scipy】scipy.linalg.slove 求解线性方程组 python

另一种方法，scipy寻根函数求方程组的解: 点击跳转. 用scipy.linalg.slove求解问题：求解下列线性方程组 3 x + 2 y = 2 3x+2y=2 3x+2y=2 x − y = 4 x-y=4 x−y=4 5 y + z = − 1 5y+z=-1 5y+z=−1 程序，如下 import numpy as npa = np.array([[3, 2,

超松驰迭代法SOR_解线性方程组的迭代法

超松驰迭代法SOR_解线性方程组的迭代法标签：计算方法实验 #include <stdio.h>#include <math.h>#define maxn 3int main(){double a[maxn][maxn + 1], x[maxn] = {0};double eps = 1e-9, w = 1.05;int n, k, kmax = 100;freopen("gauss.t

高斯-塞德尔迭代法Gauss-Seidel_解线性方程组的迭代法

高斯-塞德尔迭代法Gauss-Seidel_解线性方程组的迭代法标签：计算方法实验 #include <stdio.h>#include <math.h>#define maxn 3int main(){double a[maxn][maxn + 1], x[maxn] = {0};double eps = 1e-9;int n, k, kmax = 100;freopen("gauss

改进的平方根法_解线性方程组的直接解法

改进的平方根法_解线性方程组的直接解法标签：计算方法实验 #include <stdio.h>#include <math.h>const int maxn = 15;int main(){double a[maxn][maxn], b[maxn], y[maxn], x[maxn], l[maxn][maxn], d[maxn];int n, sum;freopen("sqrt.txt"

平方根法乔累斯基分解Cholesky_解线性方程组的直接解法

平方根法乔累斯基分解Cholesky_解线性方程组的直接解法标签：计算方法实验 #include <stdio.h>#include <math.h>const int maxn = 15;int main(){double a[maxn][maxn], b[maxn], y[maxn], x[maxn], l[maxn][maxn];int n, sum;freopen("sqrt.t

杜利特尔分解Doolittle转化为克洛特分解Crout_解线性方程组的直接解法

杜利特尔分解Doolittle转化为克洛特分解Crout_解线性方程组的直接解法标签：计算方法实验 #include <stdio.h>#include <string.h>#include <math.h>const int maxn = 15;int main(){double a[maxn][maxn], b[maxn], y[maxn], x[maxn], l[maxn][max

克洛特分解法Crout_解线性方程组的直接解法

克洛特分解法Crout_解线性方程组的直接解法标签：计算方法实验 #include <stdio.h>#include <math.h>const int maxn = 15;int main(){double a[maxn][maxn], b[maxn], y[maxn], x[maxn], l[maxn][maxn], u[maxn][maxn];int i, j, k, r, n,

R语言求解混合线性方程组（有系谱）

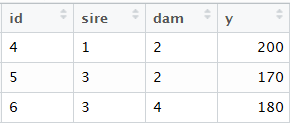
用矩阵混合线性方程组计算：方差组分已知数据 Y = Xb + Za + e > dat <- data.frame(id=c(4,5,6),sire = c(1,3,3),dam=c(2,2,4),y=c(200,170,180))> dat id sire dam y1 4 1 2 2002 5 3 2 1703 6 3 4 180>

$大名鼎鼎的LU分解——Matlab解线性方程组（3）$