本文主要是介绍平方根法 乔累斯基分解Cholesky_解线性方程组的直接解法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
平方根法 乔累斯基分解Cholesky_解线性方程组的直接解法
标签:计算方法实验
#include <stdio.h>
#include <math.h>const int maxn = 15;int main(){double a[maxn][maxn], b[maxn], y[maxn], x[maxn], l[maxn][maxn];int n, sum;freopen("sqrt.txt", "r", stdin);scanf("%d", &n);for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++) scanf("%lf", &a[i][j]);scanf("%lf", &b[i]);}/*for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++) printf("%10f", a[i][j]);printf("%10f\n", b[i]);}*/for(int i = 1; i <= n; i++){ //算L: 对正定矩阵A分解,A = LL^Tsum = 0;for(int k = 1; k <= i - 1; k++) sum += (l[i][k] * l[i][k]);l[i][i] = sqrt(a[i][i] - sum);sum = 0;for(int j = i + 1; j <= n; j++){for(int k = 1; k <= i - 1; k++) sum += (l[j][k] * l[i][k]);l[j][i] = (a[j][i] - sum) / l[i][i];}}for(int i = 1; i <= n; i++){ //求y: A = LL^T -> LL^Tx = b -> Ly = bsum = 0;for(int k = 1; k <= i - 1; k++) sum += (l[i][k] * y[k]);y[i] = (b[i] - sum) / l[i][i];}for(int i = n; i >= 1; i--){ //求x: L^Tx = ysum = 0;for(int k = i + 1; k <= n; k++) sum += (l[k][i] * x[k]);x[i] = (y[i] - sum) / l[i][i];}for(int i = 1; i <= n; i++) printf("%10f\n", x[i]);return 0;
}
数据文件
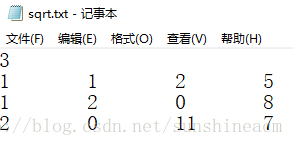
实验结果
这篇关于平方根法 乔累斯基分解Cholesky_解线性方程组的直接解法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
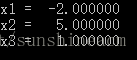


![[项目][CMP][直接向堆申请页为单位的大块内存]详细讲解](/front/images/it_default.gif)




