OpenGL/GLUT实践：流体模拟——数值解法求解Navier-Stokes方程模拟二维流体（电子科技大学信软图形与动画Ⅱ实验）

本文主要是介绍OpenGL/GLUT实践：流体模拟——数值解法求解Navier-Stokes方程模拟二维流体（电子科技大学信软图形与动画Ⅱ实验），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

源码见GitHub：A-UESTCer-s-Code

文章目录

- 1 实现效果
- 2 实现过程
- - 2.1 流体模拟实现
  - - 2.1.1 网格结构
    - 2.1.2 数据结构
    - 2.1.3 程序结构
    - - 1) 更新速度场
      - 2) 更新密度值
    - 2.1.4 实现效果
  - 2.2 颜色设置
  - - 2.2.1 颜色绘制
    - 2.2.2 颜色交互
    - 2.2.3 实现效果
  - 2.3 障碍设置
  - - 2.3.1 障碍定义
    - 2.3.2 障碍边界条件判定
    - 2.3.3 障碍实现
    - 2.3.4 障碍绘制
    - 2.3.5 增加上吹风
    - 2.3.6 实现效果

1 实现效果

最终的实现效果如下：
111

2 实现过程

2.1 流体模拟实现

2.1.1 网格结构

在流体模拟中，使用一个 $\times (N + 2)$ 的网格来表示流体的运动和属性。每个网格单元中心定义了该网格内的流体速度场（水平和垂直速度分量）以及密度值。网格的最外层用于表示边界条件，以便模拟封闭盒子内的流体流动。

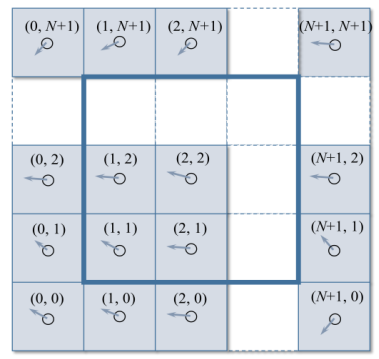
2.1.2 数据结构

Stam 定义了两个大小为 $\times (N + 2)$ 的数组来存储网格中流体的速度场和密度值。为了提高计算效率，数据以一维数组的形式存储。具体定义如下：

static float *u, *v, *u_prev, *v_prev;
static float *dens, *dens_prev;

其中：

u 和 v 是指向一维数组的指针，分别存储当前速度场的 x 方向和 y 方向分量值。
u_prev 和 v_prev 是指向一维数组的指针，分别存储前一时刻的速度场分量值。
dens 是指向一维数组的指针，存储当前时刻的密度值。
dens_prev 是指向一维数组的指针，存储前一时刻的密度值。

为了分配所需要的内存空间，定义了如下函数 allocate_data：

static int allocate_data (void) {int size = (N + 2) * (N + 2);u = (float *) malloc(size * sizeof(float));v = (float *) malloc(size * sizeof(float));u_prev = (float *) malloc(size * sizeof(float));v_prev = (float *) malloc(size * sizeof(float));dens = (float *) malloc(size * sizeof(float));dens_prev = (float *) malloc(size * sizeof(float));if (!u || !v || !u_prev || !v_prev || !dens || !dens_prev) {fprintf(stderr, "Cannot allocate data\n");return 0;}return 1;
}

size = (N + 2) * (N + 2);：计算数组的大小。N是数组的维度，+2是为了在数组的边界添加额外的空间。
u、v、u_prev、v_prev、dens和dens_prev：这些都是浮点数数组，用malloc函数分配内存。每个数组的大小都是size * sizeof(float)，即数组元素数量乘以每个元素的大小。
barrier：这是一个整数数组，用malloc函数分配内存。数组的大小是(N + 2) * (N + 2) * sizeof(int)。
if (!u || !v || !u_prev || !v_prev || !dens || !dens_prev)：这是一个错误检查。如果任何一个malloc调用失败，它会返回NULL，这个if语句就会成立。如果成立，它会打印一条错误消息，并返回0表示失败。
return (1);：如果所有的malloc调用都成功，函数就会返回1表示成功。

这个函数分配了存储当前和之前时刻速度场和密度值的空间，并检查每个指针是否分配成功。如果有任何一个指针分配失败，函数会输出错误信息并返回 0。

为了方便根据索引值读取数组中的元素，它用于计算二维数组在一维数组中的索引。定义了如下宏：

#define IX(i, j) ((i) + (N + 2) * (j))

在这个宏中，i和j是二维数组的行和列索引，N+2是二维数组的列数。所以，IX(i,j)的结果是i + (N+2)*j，这是一个常见的将二维数组索引转换为一维数组索引的公式。

例如：为了读取当前时刻第 i 行和第 j 列的网格（i, j）中速度场的 x 方向分量值，可以简单地通过 u[IX(i, j)] 进行访问。

2.1.3 程序结构

程序的主要结构如下。首先，通过 get_from_UI 函数利用用户点击鼠标的信息来初始化密度值和速度场，然后通过 vel_step 和 dens_step 函数更新速度场与密度的状态，最后绘制密度。

static void idle_func (void) {get_from_UI(dens_prev, u_prev, v_prev);vel_step(N, u, v, u_prev, v_prev, visc, dt);dens_step(N, dens, dens_prev, u, v, diff, dt);// 其他代码
}

1) 更新速度场

更新速度场的程序框架如图所示。每个时间步需要计算外力项，然后计算扩散项和平流项。具体实现通过 vel_step 函数完成：

void vel_step(int N, float *u, float *v, float *u0, float *v0, float visc, float dt) {add_source(N, u, u0, dt);add_source(N, v, v0, dt);SWAP(u0, u);diffuse(N, 1, u, u0, visc, dt);SWAP(v0, v);diffuse(N, 2, v, v0, visc, dt);project(N, u, v, u0, v0);SWAP(u0, u);SWAP(v0, v);advect(N, 1, u, u0, u0, v0, dt);advect(N, 2, v, v0, u0, v0, dt);project(N, u, v, u0, v0);
}

外力添加：

add_source 函数实现了外力的添加：

void add_source(int N, float *x, float *s, float dt) {int i, size = (N + 2) * (N + 2);for (i = 0; i < size; i++) {x[i] += dt * s[i];}
}

完成外力添加后，需要交换速度场两个分量 u0、u 和 v0、v 的数值。SWAP 是一个宏定义，用于交换两个数组的指针：

#define SWAP(x0, x) {float *tmp = x0; x0 = x; x = tmp;}

扩散项计算：

接下来计算扩散项，扩散系数保存在变量 diff 中。根据公式，网格 (i, j) 中速度场与周围相邻的四个网格相关。假设整个网格长度为 1，每个网格长度为 1/N，那么 a = dt * diff * N * N。扩散项由 diffuse 函数实现：

void diffuse(int N, int b, float *x, float *x0, float diff, float dt) {float a = dt * diff * N * N;lin_solve(N, b, x, x0, a, 1 + 4 * a);
}

lin_solve 函数实现 Poisson 方程求解：

void lin_solve(int N, int b, float *x, float *x0, float a, float c) {int i, j, k;for (k = 0; k < 20; k++) {FOR_EACH_CELLx[IX(i, j)] = (x0[IX(i, j)] + a * (x[IX(i - 1, j)] + x[IX(i + 1, j)] + x[IX(i, j - 1)] + x[IX(i, j + 1)])) / c;END_FORset_bnd(N, b, x);}
}

FOR_EACH_CELL 和 END_FOR 是宏定义，用于遍历所有网格：

#define FOR_EACH_CELL for (i = 1; i <= N; i++) { for (j = 1; j <= N; j++) {
#define END_FOR }}

set_bnd 函数用于设置边界条件，将在后面详细讲解。

平流项计算：

最后一步计算平流项，采用隐式积分法，逆时追踪粒子轨道，在新位置通过双线性插值求得平流项的值。具体实现如下：

void advect(int N, int b, float *d, float *d0, float *u, float *v, float dt) {int i, j, i0, j0, i1, j1;float x, y, s0, t0, s1, t1, dt0;dt0 = dt * N;FOR_EACH_CELLx = i - dt0 * u[IX(i, j)];y = j - dt0 * v[IX(i, j)];if (x < 0.5f) x = 0.5f;if (x > N + 0.5f) x = N + 0.5f;i0 = (int)x;i1 = i0 + 1;if (y < 0.5f) y = 0.5f;if (y > N + 0.5f) y = N + 0.5f;j0 = (int)y;j1 = j0 + 1;s1 = x - i0;s0 = 1 - s1;t1 = y - j0;t0 = 1 - t1;d[IX(i, j)] = s0 * (t0 * d0[IX(i0, j0)] + t1 * d0[IX(i0, j1)]) +s1 * (t0 * d0[IX(i1, j0)] + t1 * d0[IX(i1, j1)]);END_FORset_bnd(N, b, d);
}

完成了外力计算、扩散项计算以及平流项计算后，最后对结果进行投射。根据公式，投射由 project 函数实现：

void project(int N, float *u, float *v, float *p, float *div) {int i, j;FOR_EACH_CELLdiv[IX(i, j)] = -0.5f * (u[IX(i + 1, j)] - u[IX(i - 1, j)] + v[IX(i, j + 1)] - v[IX(i, j - 1)]) / N;p[IX(i, j)] = 0;END_FORset_bnd(N, 0, div);set_bnd(N, 0, p);lin_solve(N, 0, p, div, 1, 4);FOR_EACH_CELLu[IX(i, j)] -= 0.5f * N * (p[IX(i + 1, j)] - p[IX(i - 1, j)]);v[IX(i, j)] -= 0.5f * N * (p[IX(i, j + 1)] - p[IX(i, j - 1)]);END_FORset_bnd(N, 1, u);set_bnd(N, 2, v);
}

在 project 函数中，再次调用了 lin_solve 函数求解 Poisson 压力方程，然后利用公式求解出散度为 0 的速度场。

vel_step 函数调用了两次 project 函数。这是因为如果能让速度场保持物质守恒，advect 函数计算结果将会更准确。

边界条件设置：

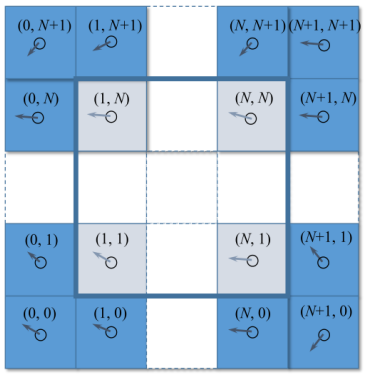
最后，更新边界处的速度场由 set_bnd 函数实现：

void set_bnd(int N, int b, float *x) {int i;for (i = 1; i <= N; i++) {x[IX(0, i)] = b == 1 ? -x[IX(1, i)] : x[IX(1, i)];x[IX(N + 1, i)] = b == 1 ? -x[IX(N, i)] : x[IX(N, i)];x[IX(i, 0)] = b == 2 ? -x[IX(i, 1)] : x[IX(i, 1)];x[IX(i, N + 1)] = b == 2 ? -x[IX(i, N)] : x[IX(i, N)];}x[IX(0, 0)] = 0.5f * (x[IX(1, 0)] + x[IX(0, 1)]);x[IX(0, N + 1)] = 0.5f * (x[IX(1, N + 1)] + x[IX(0, N)]);x[

2) 更新密度值

根据密度更新方程 (6-32)，密度更新流程的程序框架如下图所示。每个时间步需要计算新增加的密度值项，然后计算密度的扩散项以及密度随着速度场的移动。

密度更新基本架构：

具体实现通过 dens_step 函数完成：

void dens_step(int N, float *x, float *x0, float *u, float *v, float diff, float dt) {add_source(N, x, x0, dt);SWAP(x0, x);diffuse(N, 0, x, x0, diff, dt);SWAP(x0, x);advect(N, 0, x, x0, u, v, dt);
}

新增加密度值的计算：

计算新增加的密度值仍然由 add_source 函数实现。add_source 函数利用外部源对密度值进行修改，外部源密度存储在指针 x0 指向的数组中。

void add_source(int N, float *x, float *s, float dt) {int i, size = (N + 2) * (N + 2);for (i = 0; i < size; i++) {x[i] += dt * s[i];}
}

密度扩散项的计算：

密度扩散项与速度场扩散项非常类似，通过 diffuse 函数模拟密度的扩散。密度扩散系数为 diff，当 diff > 0 时，密度将会扩散到周围。每个网格只与其周围直接相邻的四个网格交换密度。网格内密度值随着密度扩散至相邻网格而降低，随着相邻网格密度流入而增加。

void diffuse(int N, int b, float *x, float *x0, float diff, float dt) {float a = dt * diff * N * N;lin_solve(N, b, x, x0, a, 1 + 4 * a);
}

密度平流项的计算：

密度平流项与速度场平流项类似，通过调用 advect 函数实现密度的对流项计算。

void advect(int N, int b, float *d, float *d0, float *u, float *v, float dt) {int i, j, i0, j0, i1, j1;float x, y, s0, t0, s1, t1, dt0;dt0 = dt * N;FOR_EACH_CELLx = i - dt0 * u[IX(i, j)];y = j - dt0 * v[IX(i, j)];if (x < 0.5f) x = 0.5f;if (x > N + 0.5f) x = N + 0.5f;i0 = (int)x;i1 = i0 + 1;if (y < 0.5f) y = 0.5f;if (y > N + 0.5f) y = N + 0.5f;j0 = (int)y;j1 = j0 + 1;s1 = x - i0;s0 = 1 - s1;t1 = y - j0;t0 = 1 - t1;d[IX(i, j)] = s0 * (t0 * d0[IX(i0, j0)] + t1 * d0[IX(i0, j1)]) +s1 * (t0 * d0[IX(i1, j0)] + t1 * d0[IX(i1, j1)]);END_FORset_bnd(N, b, d);
}

通过以上步骤，完成了新增加密度值的计算、密度的扩散以及密度的平流。整个密度更新流程与速度场的更新流程类似，确保了密度值在模拟过程中能够正确反映流体的运动特性。

2.1.4 实现效果

具体的实现效果如下：

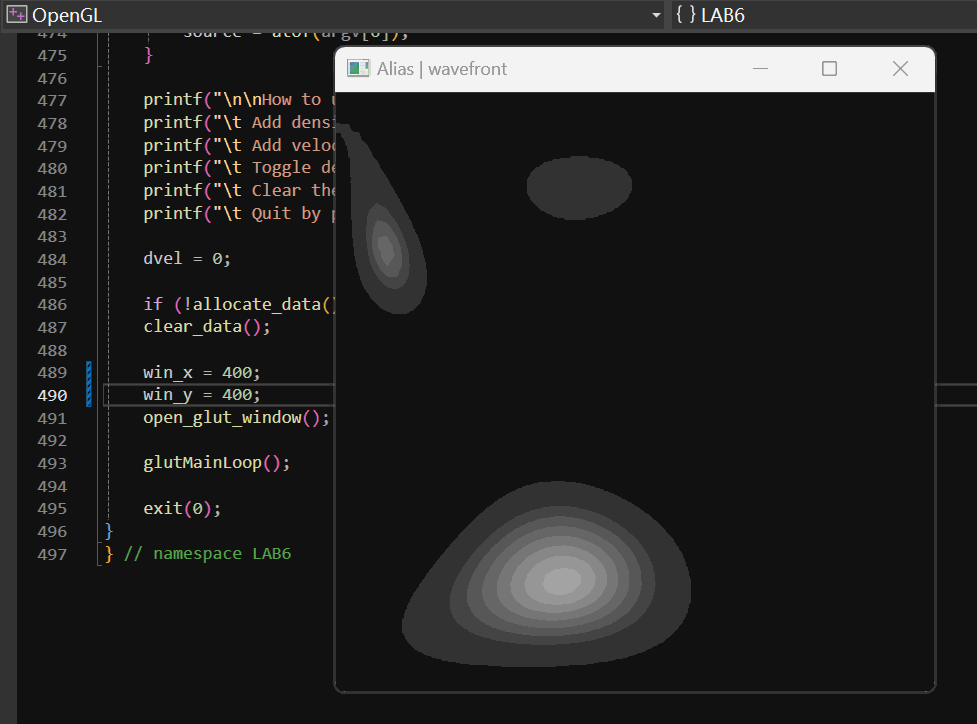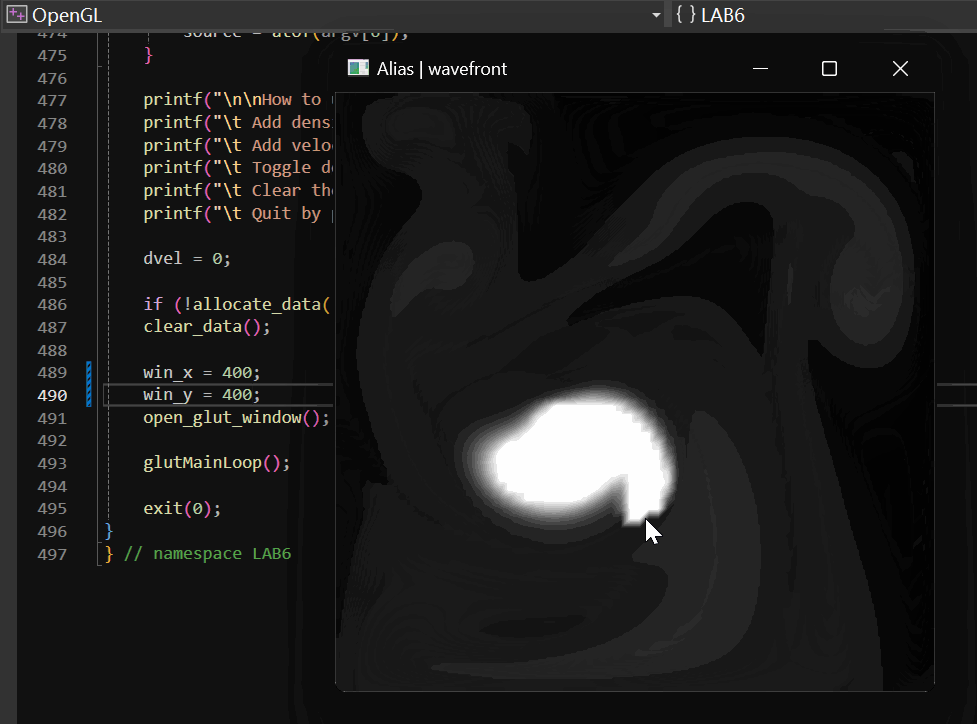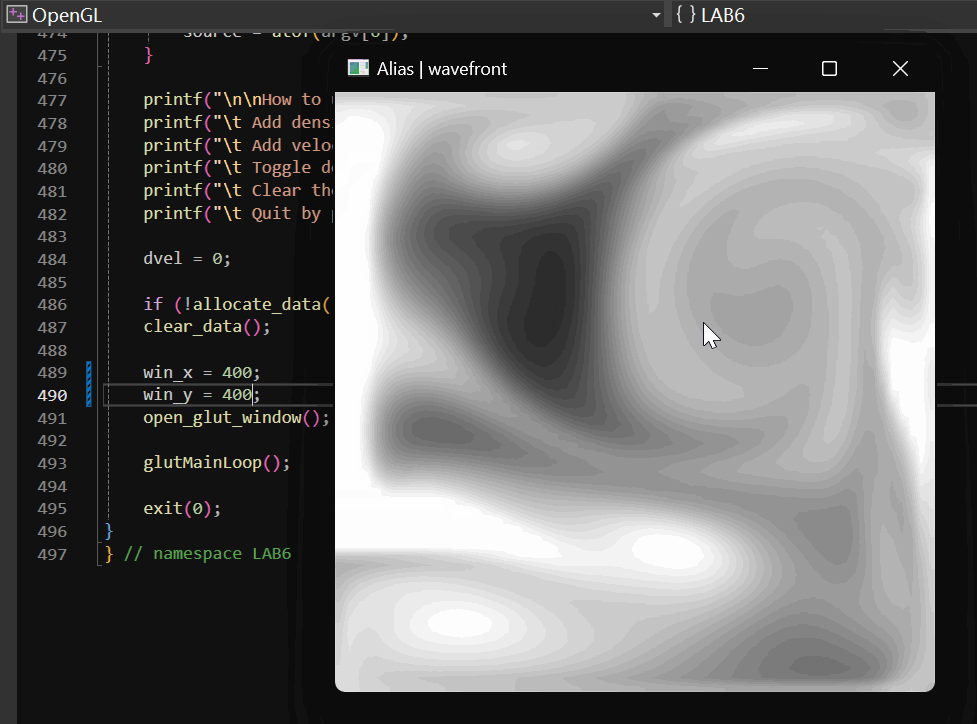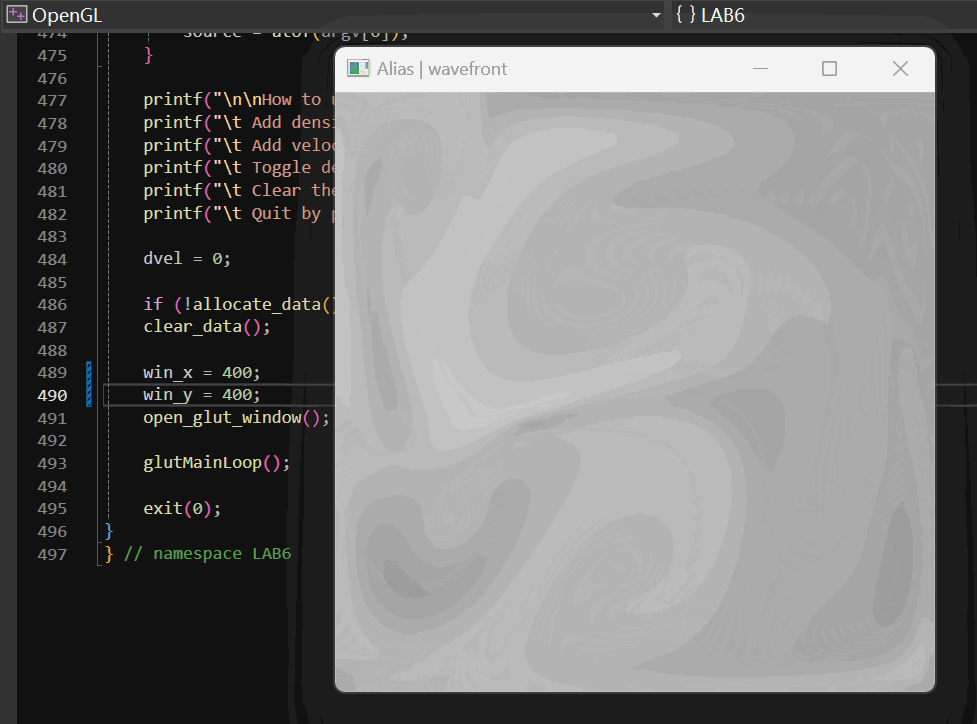
2.2 颜色设置

颜色的设置主要出现在draw_density和get_from_UI两个函数中。先设置一个颜色的全局变量：

float currentColor[3] = { 1.0f, 1.0f, 1.0f }; // 默认为白色

2.2.1 颜色绘制

在draw_density函数中，颜色的设置是基于密度dens和当前颜色currentColor的。对于每个顶点，它都会计算一个颜色值，这个颜色值是密度值和当前颜色的各分量的乘积。例如，d00 * currentColor[0]计算的是红色分量，d00 * currentColor[1]计算的是绿色分量，d00 * currentColor[2]计算的是蓝色分量。这样，颜色的强度会根据密度的大小变化。

glColor3f(d00 * currentColor[0], d00 * currentColor[1], d00 * currentColor[2]); glVertex2f(x, y);
glColor3f(d10 * currentColor[0], d10 * currentColor[1], d10 * currentColor[2]); glVertex2f(x + h, y);
glColor3f(d11 * currentColor[0], d11 * currentColor[1], d11 * currentColor[2]); glVertex2f(x + h, y + h);
glColor3f(d01 * currentColor[0], d01 * currentColor[1], d01 * currentColor[2]); glVertex2f(x, y + h);

2.2.2 颜色交互

在get_from_UI函数中，当鼠标按下时，会根据鼠标的位置来设置currentColor。currentColor[0] = (float)mx / win_x;设置的是红色分量，currentColor[1] = (float)my / win_y;设置的是绿色分量，currentColor[2] = 0.5f;设置的是蓝色分量。这样，颜色会随着鼠标的位置变化。

if (mouse_down[0])
{u[IX(i, j)] = force * (mx - omx);v[IX(i, j)] = force * (omy - my);currentColor[0] = (float)mx / win_x;currentColor[1] = (float)my / win_y;currentColor[2] = 0.5f;
}

currentColor[0] = (float)mx / win_x;：设置当前颜色的红色分量。新的值是鼠标在x方向的位置mx除以窗口宽度win_x。
currentColor[1] = (float)my / win_y;：设置当前颜色的绿色分量。新的值是鼠标在y方向的位置my除以窗口高度win_y。
currentColor[2] = 0.5f;：设置当前颜色的蓝色分量为0.5。

当鼠标左键被按下时，它会根据鼠标的移动来更新速度场，并根据鼠标的位置来设置当前颜色。

2.2.3 实现效果

实现效果如下：

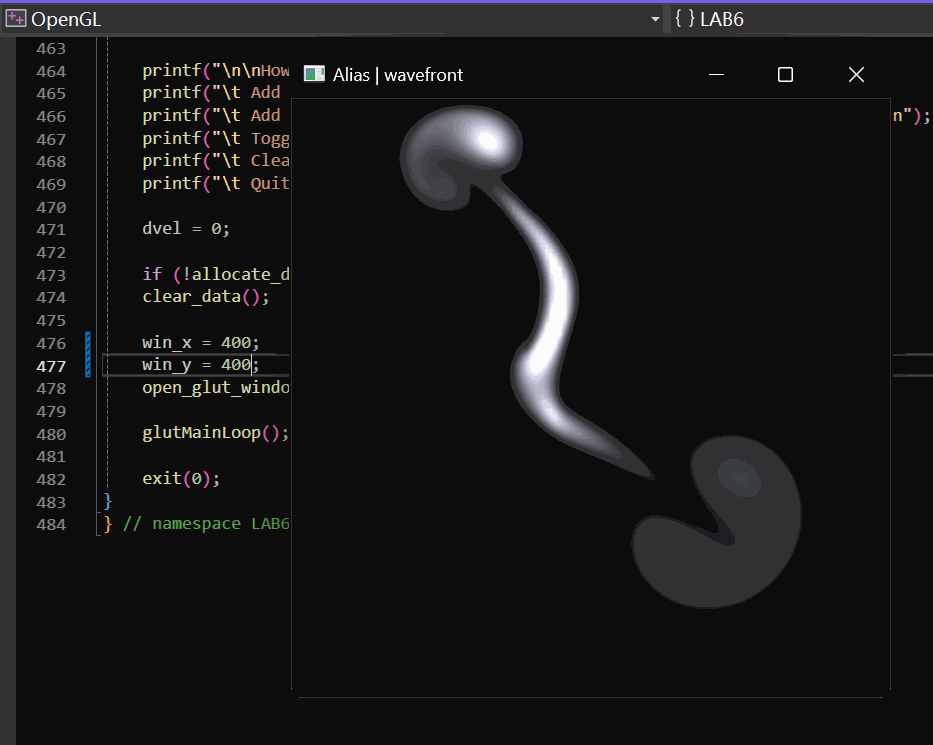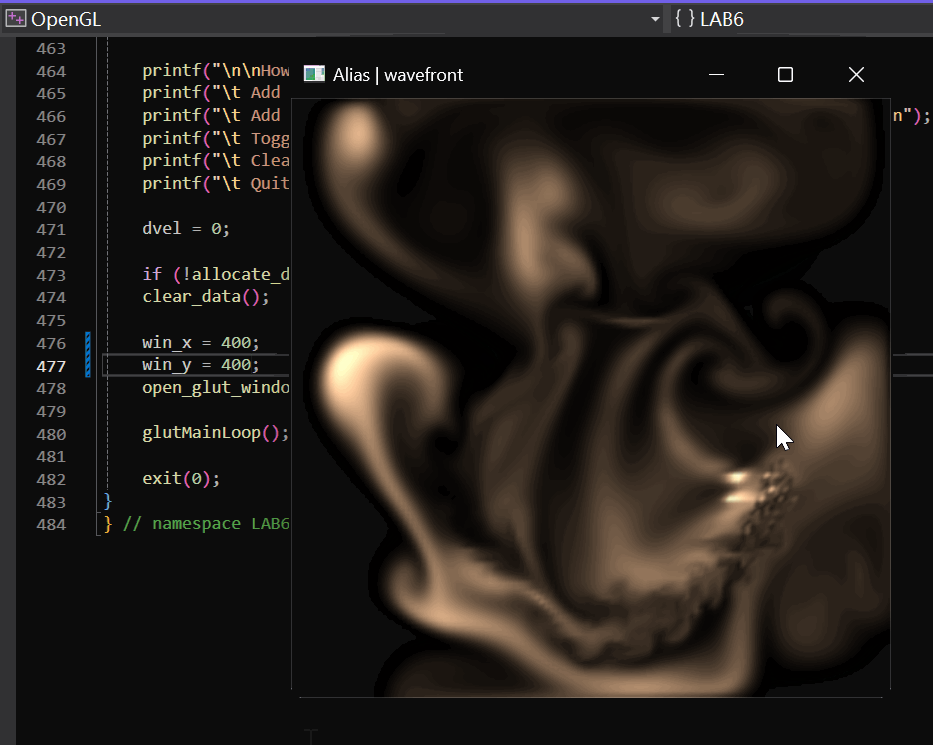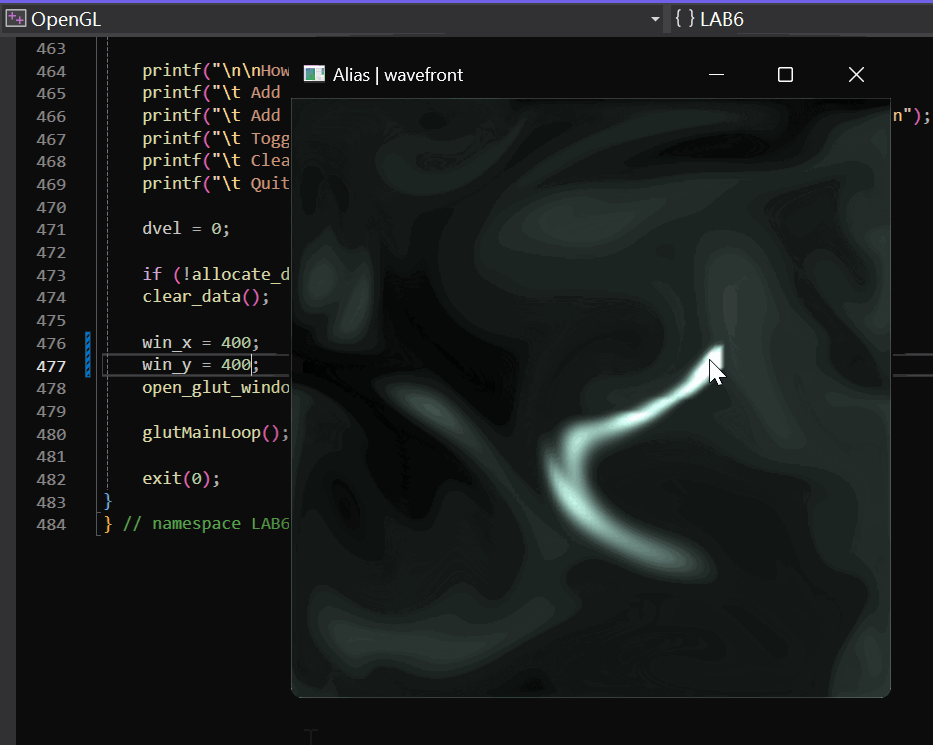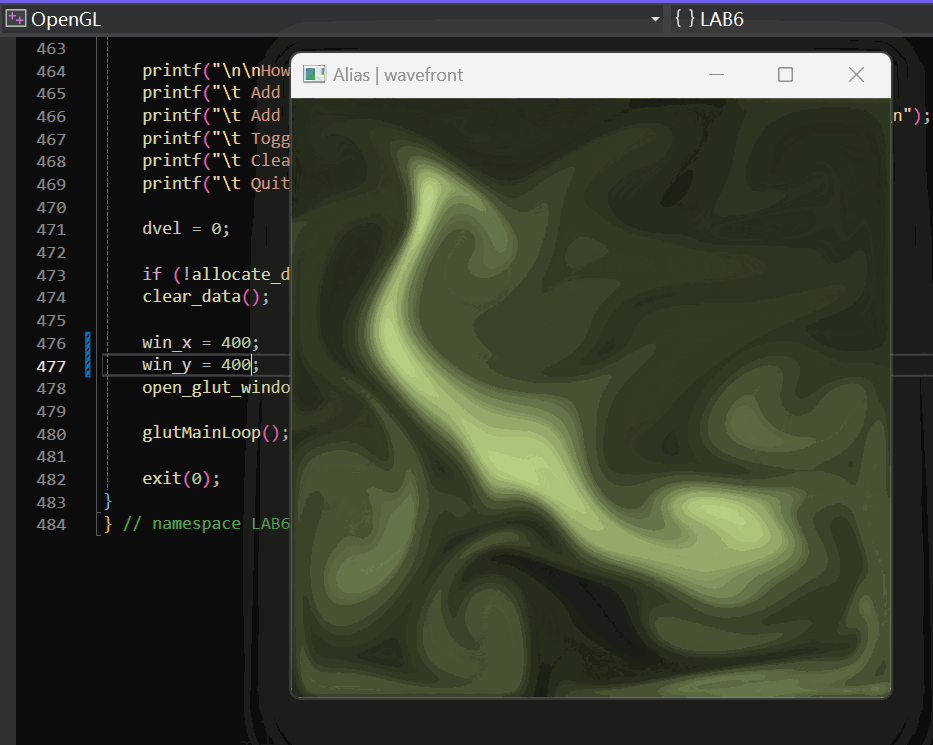
2.3 障碍设置

2.3.1 障碍定义

首先定义一些障碍需要使用的宏：

#define MIDDLE (N / 2)    
#define HOLE1_START (N / 4)
#define HOLE1_END (N / 4 + 5)
#define HOLE2_START (3 * N / 4)
#define HOLE2_END (3 * N / 4 + 5)

这些宏定义用于简化代码中的常量表达。具体而言：

MIDDLE：网格的中间行或列索引，即 N / 2。
HOLE1_START 和 HOLE1_END：第一个孔洞的起始和结束位置，位于网格的 N / 4 和 N / 4 + 5 之间。
HOLE2_START 和 HOLE2_END：第二个孔洞的起始和结束位置，位于网格的 3 * N / 4 和 3 * N / 4 + 5 之间。

barrier数组定义：

int* barrier; // 数组表示隔板的位置

barrier：一个整型指针，表示一个数组，用于存储每个网格点是否有隔板的位置。数组中的值为 1 表示有隔板，为 0 表示没有隔板。

2.3.2 障碍边界条件判定

set_bnd 函数用于设置边界条件。函数的参数为网格大小 N，边界类型 b（用于区分速度场分量的边界条件），以及要处理的数组 x（存储流体的某一物理量，如速度或密度）。我们在其基础上对其增加处理网格中间的隔板的功能。

static void set_bnd(int N, int b, float* x)
{int i, j;for (i = 1; i <= N; i++){if (barrier[IX(0, i)] == 0)x[IX(0, i)] = b == 1 ? -x[IX(1, i)] : x[IX(1, i)];if (barrier[IX(N + 1, i)] == 0)x[IX(N + 1, i)] = b == 1 ? -x[IX(N, i)] : x[IX(N, i)];if (barrier[IX(i, 0)] == 0)x[IX(i, 0)] = b == 2 ? -x[IX(i, 1)] : x[IX(i, 1)];if (barrier[IX(i, N + 1)] == 0)x[IX(i, N + 1)] = b == 2 ? -x[IX(i, N)] : x[IX(i, N)];// 处理中间隔板位置if (barrier[IX(i, MIDDLE)] == 1){if (b == 1){x[IX(i, MIDDLE)] = -x[IX(i, MIDDLE + 1)];}else if (b == 2){x[IX(i, MIDDLE)] = -x[IX(i, MIDDLE - 1)];}else{x[IX(i, MIDDLE)] = 0;}}}// 处理角落的情况x[IX(0, 0)] = 0.5f * (x[IX(1, 0)] + x[IX(0, 1)]);x[IX(0, N + 1)] = 0.5f * (x[IX(1, N + 1)] + x[IX(0, N)]);x[IX(N + 1, 0)] = 0.5f * (x[IX(N, 0)] + x[IX(N + 1, 1)]);x[IX(N + 1, N + 1)] = 0.5f * (x[IX(N, N + 1)] + x[IX(N + 1, N)]);
}

边界处理：

if (barrier[IX(0, i)] == 0)x[IX(0, i)] = b == 1 ? -x[IX(1, i)] : x[IX(1, i)];
if (barrier[IX(N + 1, i)] == 0)x[IX(N + 1, i)] = b == 1 ? -x[IX(N, i)] : x[IX(N, i)];
if (barrier[IX(i, 0)] == 0)x[IX(i, 0)] = b == 2 ? -x[IX(i, 1)] : x[IX(i, 1)];
if (barrier[IX(i, N + 1)] == 0)x[IX(i, N + 1)] = b == 2 ? -x[IX(i, N)] : x[IX(i, N)];

当 barrier 数组在相应位置为 0 时，表示此处没有隔板，应用一般的边界条件。
对于速度场的分量，b 为 1 或 2 时分别处理 u 和 v 分量，负号表示反向速度以实现无滑移条件。

处理中间隔板位置：

if (barrier[IX(i, MIDDLE)] == 1)
{if (b == 1){x[IX(i, MIDDLE)] = -x[IX(i, MIDDLE + 1)];}else if (b == 2){x[IX(i, MIDDLE)] = -x[IX(i, MIDDLE - 1)];}else{x[IX(i, MIDDLE)] = 0;}
}

当 barrier 数组在相应位置为 1 时，表示此处有隔板。
如果 b == 1，表示处理 u 分量，将其设为与中间右侧网格点的 u 分量相反。
如果 b == 2，表示处理 v 分量，将其设为与中间左侧网格点的 v 分量相反。
否则，将中间网格点的值设为 0。

处理角落：

x[IX(0, 0)] = 0.5f * (x[IX(1, 0)] + x[IX(0, 1)]);
x[IX(0, N + 1)] = 0.5f * (x[IX(1, N + 1)] + x[IX(0, N)]);
x[IX(N + 1, 0)] = 0.5f * (x[IX(N, 0)] + x[IX(N + 1, 1)]);
x[IX(N + 1, N + 1)] = 0.5f * (x[IX(N, N + 1)] + x[IX(N + 1, N)]);

设置角落处的值为相邻两个边界点值的平均值，以确保流体在角落处的连续性。

2.3.3 障碍实现

在流体模拟中，障碍物的实现通过在网格中设置障碍标记来实现。在clear_data 函数中的隔板设置使在中间位置加入带有两个开孔的隔板。

static void clear_data(void)
{// 其他初始化代码// ...// 在中间位置加入隔板，假设有两个开孔for (i = 0; i <= N + 1; i++){if ((i >= HOLE1_START && i <= HOLE1_END) || (i >= HOLE2_START && i <= HOLE2_END)){barrier[IX(i, MIDDLE)] = 0; // 开孔}else{barrier[IX(i, MIDDLE)] = 1; // 隔板}}
}

这个循环遍历从 0 到 N+1 的所有索引，设置中间行（MIDDLE）的隔板和开孔。
对于在 HOLE1_START 到 HOLE1_END 以及 HOLE2_START 到 HOLE2_END 范围内的索引，设置 barrier[IX(i, MIDDLE)] = 0，表示这些位置是开孔。
对于不在上述范围内的索引，设置 barrier[IX(i, MIDDLE)] = 1，表示这些位置是隔板。

通过这种方式，网格的中间位置（MIDDLE 行）将形成一个带有两个开孔的隔板结构。

2.3.4 障碍绘制

draw_barrier 函数实现了绘制带有隔板的流体模拟中的障碍物：

static void draw_barrier(void)
{int i;float h = 1.0f / N;glColor3f(0.7f, 0.7f, 0.7f); // 设置颜色为灰色glLineWidth(5.0f); // 设置线宽为5.0glBegin(GL_LINES); // 开始绘制线段for (i = 0; i <= N; i++){// 如果不在开孔的位置if (!((i >= HOLE1_START && i <= HOLE1_END) || (i >= HOLE2_START && i <= HOLE2_END))){glVertex2f(i * h, MIDDLE * h - 0.5f * h); // 绘制线段的起点glVertex2f(i * h, MIDDLE * h + 0.5f * h); // 绘制线段的终点}}glEnd(); // 结束绘制
}

glColor3f(0.7f, 0.7f, 0.7f);：设置绘制颜色为灰色。
glLineWidth(5.0f);：设置线段的宽度为5.0。
glBegin(GL_LINES);：开始绘制线段。
循环遍历从 0 到 N 的所有索引 i，绘制隔板的部分。
- 如果 i 不在任何一个开孔的范围内，则绘制隔板的线段。
- 隔板的线段起点是 (i * h, MIDDLE * h - 0.5f * h)，终点是 (i * h, MIDDLE * h + 0.5f * h)。
glEnd();：结束绘制线段。

通过这段代码，隔板部分被绘制成一系列的竖直线段，形成一个连续的隔板结构。这样，可以在流体模拟的可视化过程中清晰地展示隔板的位置和形状。

2.3.5 增加上吹风

为了使流体模拟效果更加生动，我们增加了一个向上吹的风的效果。下面是对 vel_step 函数的修改，以实现风的作用：

static void vel_step(int N, float* u, float* v, float* u0, float* v0, float visc, float dt)
{//...// 添加风的作用for (int i = 0; i <= N + 1; i++){for (int j = 0; j <= N + 1; j++){v[IX(i, j)] += 0.001f; // 添加一个向上的速度分量，大小可以调整}}// ...
}

在 add_source 步骤后，我们增加了一个循环，遍历整个网格，并将每个格点的垂直速度分量 v 增加一个常量值 0.001f，表示一个向上的风的作用。你可以根据需要调整风的大小。
其余的代码保持不变，仍然执行了原有的流体模拟步骤，包括扩散、投影和平流。这样，风的作用会与其他流体模拟效果结合在一起，形成更加逼真的流体运动效果。