navier专题
OpenGL/GLUT实践:流体模拟——数值解法求解Navier-Stokes方程模拟二维流体(电子科技大学信软图形与动画Ⅱ实验)
源码见GitHub:A-UESTCer-s-Code 文章目录 1 实现效果2 实现过程2.1 流体模拟实现2.1.1 网格结构2.1.2 数据结构2.1.3 程序结构1) 更新速度场2) 更新密度值 2.1.4 实现效果 2.2 颜色设置2.2.1 颜色绘制2.2.2 颜色交互2.2.3 实现效果 2.3 障碍设置2.3.1 障碍定义2.3.2 障碍边界条件判定2.3.3 障碍实现2.3.
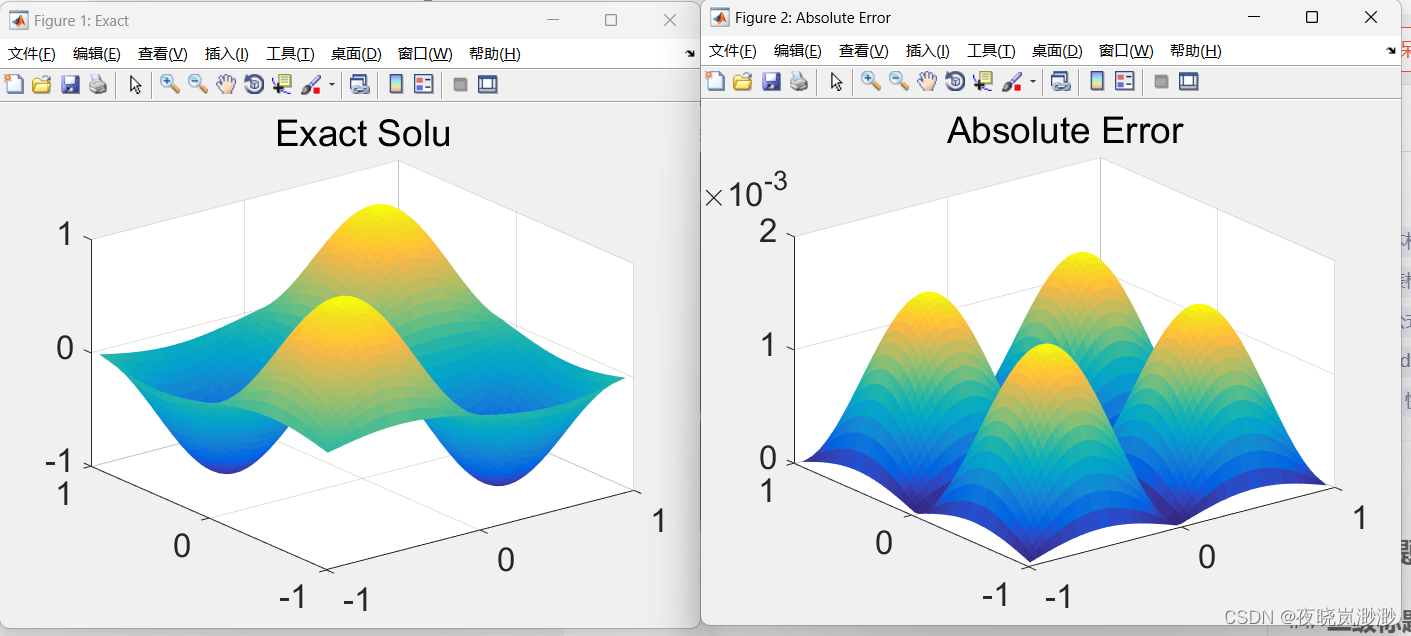
matlab:五点中心差分求解Navier边界的Biharmonic方程(具有纳维尔边界的双调和方程)
我们考虑如下形式的双调和方程的数值解 其中,Ω是欧氏空间中的多边形或多面体域,在其中,d为维度,具有分段利普希茨边界,满足内部锥条件,f(x) ∈ L2(Ω)是给定的函数,∆是标准的拉普拉斯算子。算子∆u(x)和∆2u(x)表示为 巧妙地将双调和方程(1.1)分解为两个Possion方程,传统的数值方法如有限元法(FEM)和有限差分法(FDM)在计算资源和时间复杂度较小的情况下表现良好。通过