方程专题

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【通俗理解】嵌入（Embedding）方程——自然语言处理的数学灵魂关键词提炼 #嵌入方程 #自然语言处理 #词向量 #机器学习 #神经网络 #向量空间模型 #Siri #Google翻译 #AlexNet 第一节：嵌入方程的类比与核心概念【尽可能通俗】嵌入方程可以被看作是自然语言处理中的“翻译机”，它将文本中的单词或短语转换成计算机能够理解的数学形式，即向量。正如翻译机将一种语言

OpenGL/GLUT实践：流体模拟——数值解法求解Navier-Stokes方程模拟二维流体（电子科技大学信软图形与动画Ⅱ实验）

源码见GitHub：A-UESTCer-s-Code 文章目录 1 实现效果2 实现过程2.1 流体模拟实现2.1.1 网格结构2.1.2 数据结构2.1.3 程序结构1) 更新速度场2) 更新密度值 2.1.4 实现效果 2.2 颜色设置2.2.1 颜色绘制2.2.2 颜色交互2.2.3 实现效果 2.3 障碍设置2.3.1 障碍定义2.3.2 障碍边界条件判定2.3.3 障碍实现2.3.

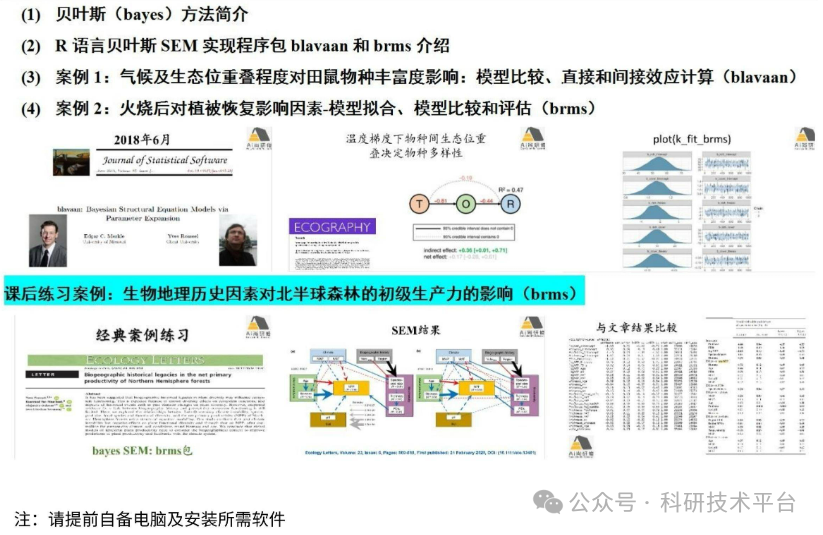
R语言结构方程模型分析与实践技术应用

结构方程模型（Sructural Equation Model）是一种建立、估计和检验研究系统中多变量间因果关系的模型方法，它可以替代多元回归、因子分析、协方差分析等方法，利用图形化模型方式清晰展示研究系统中变量间的因果网络关系，是近年来地学、生态、进化、环境、医学、社会、经济领域中应用十分广泛的统计方法。然而，自Wright在1920年美国科学院院刊（PNAS）提出第一个通径/路径（Pa

解决ax+by=c，不定方程（扩展欧几里得）

首先有几个定理我们需要知道，在这里我也会一一证明。 —————————————————————————————————————— 定理1：gcd(a,b)==gcd(b,a%b);这个是欧几里得提出并证明的。 (%是取余的意思，在数学中可用mod表示)；以下是证明过程 —————————————————————————————————————— 令a = k * b + r; （k

Python案例 | 使用四阶龙格-库塔法计算Burgers方程

使用四阶龙格-库塔法计算Burgers方程引言求解过程完整代码引言 Burgers方程产生于应用数学的各个领域，包括流体力学、非线性声学、气体动力学和交通流。它是一个基本的偏微分方程，可以通过删除压力梯度项从速度场的Navier-Stokes方程导出。对于黏度系数较小的情况( ν = 0.01 / π \nu = 0.01/ \pi ν=0.01/π)，Burgers方程会

强化学习深入学习（一）：价值函数和贝尔曼方程

文章目录 0. 引言1. 回报（Return）2. 价值函数（Value Function）3. 贝尔曼期望方程（Bellman Expectation Equation）4. 贝尔曼最优方程（Bellman Optimality Equation）总结 0. 引言强化学习（Reinforcement Learning, RL）是一种机器学习方法，通过与环境的交互来学习如何

数论 - n元线性同余方程的解法

note:n元线性同余方程因其编程的特殊性，一般在acm中用的很少，这里只是出于兴趣学了一下 n元线性同余方程的概念: 形如：(a1*x1+a2*x2+....+an*xn)%m=b%m ..................(1) 当然也有很多变形，例如：a1*x1+a2*x2+...+an*xn+m*x(n+1)=b.这两个都是等价的。判断是否有解:

Ferrari求解四次方程

参考： 1） https://proofwiki.org/wiki/Ferrari’s_Method#google_vignette 2）https://blog.csdn.net/qq_25777815/article/details/85206702

[3.2] 机器人连杆变换和运动学方程

本节首先推导相邻两连杆坐标系之间的变换矩阵，然后将这些变换矩阵依次相乘，得到操作臂的运动学方程。该方程表示末端连杆相对于基座的位姿关系，是各关节变量的函数。连杆坐标系{i}与{i-1}通过四个参数、、、联系起来，因此坐标系{i}相对于{i-1} 的齐次变换矩阵T，通常也是连

7-8 h0056. 不定方程求解

//23计科的同学们，能不能先学一下思路再自己写一下代码？给定正整数a，b，c。求不定方程 ax+by=c 关于未知数x和y的所有非负整数解组数。输入格式: 多行，每行包含三个正整数a，b，c，两个整数之间用单个空格隔开。每个数均不大于1000。输出格式: 多行，每行一个整数，即不定方程的非负整数解组数。输入样例: 2 3 18 输出样例: 4 #include<bi

比亚迪方程豹携手华为乾崑智驾，加速中国智驾技术向前

近日，比亚迪方程豹与华为乾崑智驾在深圳签署合作协议，中国两大科技巨头强强联合，共同合作开发全球首个硬派专属智能驾驶方案，实现整车智驾深度融合，首发搭载在即将上市的方程豹豹8车型。比亚迪智驾以自主研发和开放合作双线进行，加速中国智驾向前在智驾领域，比亚迪坚持独立自主研发与开放合作的双线进行。在标准化智驾平台上，比亚迪既有全栈自研的高阶智驾“天神之眼”上车，并在腾势、王朝、海洋等多款车

POJ1006同余方程基础

题目链接：http://poj.org/problem?id=1006 问题描述人自出生起就有体力，情感和智力三个生理周期，分别为23，28和33天。一个周期内有一天为峰值，在这一天，人在对应的方面（体力，情感或智力）表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日期，分别对应于体力，情感，智力出现峰值的日期。然后再给出一个起始日期，要求从这一天开始，算出最少再过

2024数学建模国赛！！！（9——差分方程模型）

资料获取方式在文章末尾！！！！！！！！！！！！！！！！！！！！！点击链接加入群聊获取资料https://qm.qq.com/q/NGl6WD0Bky

【自由能系列（初级）】自由能原理——神经科学的“能量守恒”方程

【通俗理解】自由能原理——神经科学的“能量守恒”方程关键词提炼 #自由能原理 #KL散度 #生成模型 #识别密度 #观测数据 #神经科学第一节：自由能原理的类比与核心概念 1.1 自由能原理的类比自由能原理在神经科学中的应用，可以类比为一个“大脑的能量守恒”方程。就像物理学中的能量守恒定律一样，大脑在处理信息时，也遵循着一种“自由能守恒”的原则。这个原理通过衡量大脑对外部世界的

【深入解析】最优控制中的Bellman方程——从决策到最优路径的探索

【深入解析】最优控制中的Bellman方程——从决策到最优路径的探索关键词提炼 #Bellman方程 #最优控制 #动态规划 #值函数 #策略优化 #强化学习第一节：Bellman方程的通俗解释与核心概念 1.1 通俗解释 Bellman方程是动态规划中的一个核心概念，它像是一个“未来价值指南针”，帮助我们在面对一系列决策时，找到从当前状态出发到达目标状态的最优路径。想象一下，你站

【自动驾驶】控制算法（五）连续方程离散化与离散LQR原理

写在前面： 🌟 欢迎光临清流君的博客小天地，这里是我分享技术与心得的温馨角落。📝 个人主页：清流君_CSDN博客，期待与您一同探索移动机器人领域的无限可能。 🔍 本文系清流君原创之作，荣幸在CSDN首发🐒 若您觉得内容有价值，还请评论告知一声，以便更多人受益。转载请注明出处，尊重原创，从我做起。 👍 点赞、评论、收藏，三连走一波，让我们一起养成好习惯😜 在这里，您将

推导正规方程的解

1. 准备工作 1.1 矩阵转置公式与求导公式 1.1.1 转置公式: ( m A ) T = m A T (mA)^T=mA^T (mA)T=mAT，M是常数 ( A + B ) T = A T + B T (A+B)^T = A^T + B^T (A+B)T=AT+BT ( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT ( A T ) T

提车后遇大降价被指“背刺”车主，方程豹的口碑问题何解？

进入8月下旬，汽车市场“金九银十”的销售旺季即将到来，将行业“内卷”推向新高峰。即便有宝马等高端豪华品牌退出“价格战”的先例，但为刺激销量，不少车企依旧推出了各式各样的价格优惠政策，行业内部价格竞争狼烟四起。近日，比亚迪旗下越野车品牌方程豹宣布，下调在售唯一车型豹5的售价，包括豹5探索版、领航版、云辇豪华版、云辇旗舰版在内的四款车型，均进行了5万元的价格调整，目前售价区间在23.98万至3

X§XFX§XuX§XWX§XuX§XdX§XrX§XαX§XuXpXuX§XαX§XrX§XdX§XuXWXπX§XWXeXyXeXbXπXpX§XNX§XqXeX§XrX§XαX§XuXpXuX§XαX§XrX§XeXqX§XNX§XpXπXbXeXyXeXWX§XπXWXuX§XdX§XrX§XαX§XuXpXuX§XαX§XrX§XdX§XuX§XWX§XuX§XFX§XEX§XyX§XE

中介子方程二十九

X§XFX§XuX§XWX§XuX§XdX§XrX§XαX§XuX§XαX§XrX§XdX§XuXWXπX§XWXeXyXeXbXπXpX§XNX§XqXeX§XrX§XαX§XuX§XαX§XrX§XeXqX§XNX§XpXπXbXeXyXeXWX§XπXWXuX§XdX§XrX§XαX§XuX§XαX§XrX§XdX§XuX§XWX§XuX§XFX§XEX§XyX§XEX§XrX§XαX§Xu

关于椭圆的方程（有Python画的动图）

关于椭圆的方程（有Python画的动图） flyfish 几何定义椭圆是平面上所有到两个固定点（焦点）的距离之和为常数的点的集合。这两个固定点叫做焦点。解析几何描述设椭圆的两个焦点为 F 1 F_1 F1 和 F 2 F_2 F2，焦距（两焦点之间的距离的一半）为 c c c，长轴的半长轴为 a a a，短轴的半短轴为 b b b，椭圆上任意一点到这两个焦点的距离之

关于圆的方程

关于圆的方程 flyfish 几何定义圆是平面上所有到一个固定点（圆心）距离相等的点的集合。解析几何描述设圆心位于点 ( h , k ) (h, k) (h,k)，半径为 r r r，那么对于圆上的任意一点 ( x , y ) (x, y) (x,y)，它到圆心的距离总是等于 r r r。根据勾股定理，这个距离可以表示为： ( x − h ) 2 + ( y − k ) 2

$偏微分方程算法之抛物型方程差分格式编程示例四（Richardson外推）$

方程专题

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

OpenGL/GLUT实践：流体模拟——数值解法求解Navier-Stokes方程模拟二维流体（电子科技大学信软图形与动画Ⅱ实验）

R语言结构方程模型分析与实践技术应用

解决ax+by=c，不定方程（扩展欧几里得）

Python案例 | 使用四阶龙格-库塔法计算Burgers方程

强化学习深入学习（一）：价值函数和贝尔曼方程

数论 - n元线性同余方程的解法

Ferrari求解四次方程

[3.2] 机器人连杆变换和运动学方程

7-8 h0056. 不定方程求解

比亚迪方程豹携手华为乾崑智驾，加速中国智驾技术向前

POJ1006同余方程基础

2024数学建模国赛！！！（9——差分方程模型）

【自由能系列（初级）】自由能原理——神经科学的“能量守恒”方程

【深入解析】最优控制中的Bellman方程——从决策到最优路径的探索

【自动驾驶】控制算法（五）连续方程离散化与离散LQR原理

推导正规方程的解

提车后遇大降价被指“背刺”车主，方程豹的口碑问题何解？

中介子方程三十

中介子方程二十九

关于椭圆的方程（有Python画的动图）

关于圆的方程

偏微分方程算法之抛物型方程差分格式编程示例四（Richardson外推）

【数学建模】解析几何与方程模型

椭圆的标准方程与协方差矩阵的特征值和特征向量的关系

中介子方程二十二