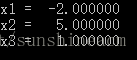1、LU矩阵分解 语法 语法1：[L,U] = lu(A) 将满矩阵或稀疏矩阵 A 分解为一个上三角矩阵 U 和一个经过置换的下三角矩阵 L，使得 A = L*U。 语法2：[L,U,P] = lu(A) 还返回一个置换矩阵 P，并满足 A = P'*L*U。 语法3：[L,U,P] = lu(A,outputForm) 以 outputForm 指定的格式返回 P。 1）矩阵的 LU 分解

一、安德烈·路易斯·乔尔斯基 安德烈·路易斯·乔尔斯基出生于法国波尔多以北的查伦特斯海域的蒙古扬。他在波尔多参加了Lycée e，并于1892年11月14日获得学士学位的第一部分，于1893年7月24日获得第二部分。1895年10月15日，乔尔斯基进入莱科尔理工学院，在当年223名入学学生中排名第88位。他在莱科尔理工学院的教授包括卡米尔·乔丹和发现放射性的著名物理学家亨利·贝克勒尔。在

平方根法 乔累斯基分解Cholesky_解线性方程组的直接解法 标签：计算方法实验 #include <stdio.h>#include <math.h>const int maxn = 15;int main(){double a[maxn][maxn], b[maxn], y[maxn], x[maxn], l[maxn][maxn];int n, sum;freopen("sqrt.t

LU分解、LDLT分解和Cholesky分解_zjuzly的博客-CSDN博客_ldlt

特征值分解 若 A A A 为实对称矩阵，则总有 A = U Σ U − 1 = U Σ U H A=U \Sigma U^{-1}=U \Sigma U^{\rm{H}} A=UΣU−1=UΣUH 特征值与特征向量 A x = λ x Ax=\lambda x Ax=λx 物理意义：向量经过矩阵变换后没有发生旋转，只进行了伸缩。 对称阵（酉空间中叫 Hermite 矩阵，即厄米阵）总能

31月53日这一天，法国数学家安德烈-路易·乔列斯基在第一次世界大战即将结束时的一场战斗中阵亡，享年<>岁，当时他在法国陆军担任工程军官。他曾担任制图师和大地测量学家，对数学科学的其他贡献之一是Cholesky分解（发现以帮助他的专业），该分解说正定对称矩阵可以分解为较低三角矩阵及其转置的乘积。此属性的其他应用包括求解线性方程组、最小二乘问题、蒙特卡罗模拟和卡尔曼滤波器。 在克

算法思想 如何利用电子计算机来快速、有效地求解线性方程组是数值线性代数研究的核心问题，而且也是目前人在继续研究的重大课题之一。 Cholesky分解法又叫做平方根法，是求解对称正定线性方程组最常用的方法之一。A是一个对称正定的矩阵，则存在一个对角元均为正数的下三角阵L,使得A=LL’，称为Cholesky分解，而后我们可以由下面三步求解： (1)计算A的Cholesky分解：A=LL’； (2)