本文主要是介绍【智能算法应用】麻雀搜索算法求解非线性方程组问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 1.算法原理
- 2.数学模型
- 3.结果展示
- 4.代码获取
1.算法原理
【智能算法】麻雀搜索算法(SSA)原理及实现
2.数学模型
非线性方程组为:
2 x 1 − x 2 = e − x 1 − x 1 + 2 x 2 = e − x 2 (1) \begin{aligned}&2x_1-x_2=e^{-x_1}\\&-x_1+2x_2=e^{-x_2}\end{aligned}\tag{1} 2x1−x2=e−x1−x1+2x2=e−x2(1)
Matlab采用fsolve函数求解:
F = @(x) [2*x(1) - x(2) - exp(-x(1));-x(1) + 2*x(2) - exp(-x(2))];
x0 = [-5,-5]'; %初始解
options = optimoptions('fsolve','Display','iter');
[x,favl] = fsolve(F,x0,options);
disp('非线性方程组解:'); disp(x);

采用优化算法求解,首要需要设计目标函数:
f i t n e s s = ( 2 x 1 − x 2 − e − x 1 ) 2 + ( − x 1 + 2 x 2 − e − x 2 ) 2 (2) fitness=(2x_1-x_2-e^{-x_1})^2+(-x_1+2x_2-e^{-x_2})^2\tag{2} fitness=(2x1−x2−e−x1)2+(−x1+2x2−e−x2)2(2)
3.结果展示

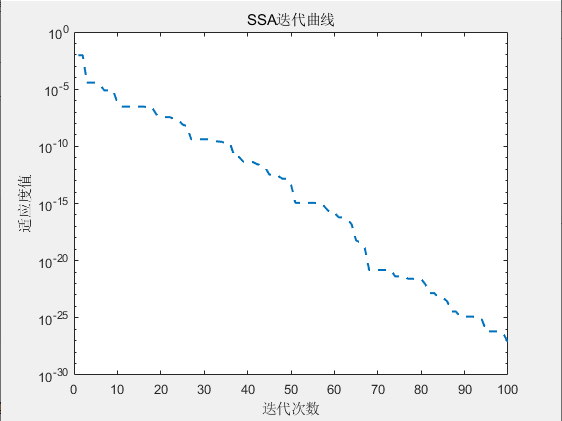
4.代码获取
这篇关于【智能算法应用】麻雀搜索算法求解非线性方程组问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







