迪杰专题
基于二叉堆优化的迪杰斯特拉算法
前言介绍 迪杰斯特拉(Dijkstra)算法是1959年由荷兰计算机科学家Dijkstra提出的算法,用于在加权图中计算从单个源点到其余节点的最短距离。采用贪心策略,每次选取到源点最近且未被访问的节点,遍历它的邻居节点更新它们到源点的最短距离,直到扩展完成。 算法诞生 在迪杰斯特拉算法出现,有这样一个问题:在荷兰的任意选取两个城市,它们的最短距离是多少?在当时,这个问题最好的算法运行时间随着
数据结构之---C语言实现最短路径之Dijkstra(迪杰斯特拉)算法
此处共有两段代码: 一、 这段代码比较全面,其中参考了github上的相关源码。可以说功能强大。 //Dijkstra(迪杰斯特拉算法)#include <stdio.h>#include <stdlib.h>#include <string.h>#define MAX 100 // 矩阵最大容量#define INF
2017年中兴算法大赛 迪杰特斯拉派
总结:本人2017年参加的比赛,对于初次参加算法大赛的作者来说,异常激动又有点小窃喜,最后在赛区拿到24名的名次,名次不算高,但是对于一步步解决问题过来的我,经验与经历更为重要,再次做一个小小的总结,也对后续算法提出自己的改进意见,希望对后面参加比赛的你们有一点点启发。 1. 试题介绍 ## 赛题 ##最强大脑中的收官蜂巢迷宫变态级挑战,相信大家都叹为观止!最强大脑收官战打响后,收视
js迪杰斯特拉算法求最短路径
1.后台生成矩阵 名词解释和下图参考:https://blog.csdn.net/csdnxcn/article/details/80057574 double[,] arr = new double[allVertices.Count(), allVertices.Count()]; //矩阵 //allVertices所有三维坐标点的集合 //lines 所有两点
【QuikGraph】C#调用第三方库实现迪杰斯特拉(Dijkstra)算法功能
QuikGraph库介绍 项目地址:https://github.com/KeRNeLith/QuikGraph API地址:https://kernelith.github.io/QuikGraph/api/index.html QuikGraph为.NET提供了通用的有向/无向图数据结构和算法。 QuikGraph提供了深度优先搜索、广度优先搜索、A*搜索、最短路径、k最短路径,最大流量、
L2-001 紧急救援(迪杰斯特拉应用)
作为一个城市的应急救援队伍的负责人,你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候,你的任务是带领你的救援队尽快赶往事发地,同时,一路上召集尽可能多的救援队。 输入格式: 输入第一行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市
最短路径问题——(弗洛伊德算法与迪杰斯特拉算法)
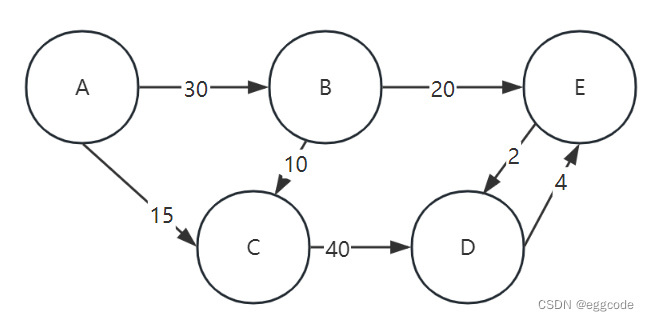
最短路径问题——(弗洛伊德算法与迪杰斯特拉算法)【板子】 题目: 对于下面的图片所给出的关系,回答下面两个问题: 利用迪杰斯特拉算法求点A到每一个点之间的最小距离。利用弗洛伊德算法求每两个点之间的最短路径。 (注意图中的A~E,分别用1~5来代替) 对于问题1(Dijkstra): 第一行输入三个数n,m,q分别表示一共有n个点,m条边,q个查询 接下来的m行每行输入三个数i,j,
【图论】Dijkstra单源最短路径-朴素方法-简单模板(迪杰斯特拉算法)
Dijkstra单源最短路径 问题描述 输入n 表示n个结点,m表示m条边,求编号1的结点到每个点的最短路径 输出从第一个点到第n个点的最短路径 思路 将图g[][]中所有的权值初始化为0x3f表示正无穷 将dist[]中所有的值初始化为0x3f表示从第一个点到所有点的距离默认为无穷 将dist[1]设置为0表示从第一个点到它自己距离为零 执行n(也就是处理n个点的次数)次如
迪杰斯特拉算法【知识点】
Dijkstra算法 1.定义 Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。注意该算法要求图中不存在负权边。 问题描述:在无向图 G=(V,E) 中,假设每
算法笔记——图、图的定义方式、图的宽度优先遍历BFS、深度优先遍历DFS、拓朴排序算法、K算法、P算法、迪杰斯特拉算法
图的算法 一、图的存储方式,如果表达图,生成图1.图的存储方式2.图的表达方式——点集、边集、图3.生成图 二、图的遍历1.图的宽度优先遍历BFS2.图的深度优先遍历DFS 三、拓朴排序算法四、最小生成树的两种算法1.Kruskal算法2.Prim算法 五、Dijkstra算法 一、图的存储方式,如果表达图,生成图 1.图的存储方式 邻接表 邻接矩阵 2.图的表达方
Python数据结构10:图,代码表示,DFS、BFS,拓朴排序,迪杰斯特拉,最小生成树,关键路径
1. 定义 “图”这个字在中文当中,指代的是图画,但是在英文当中有很多种不同的涵义。 painting:用画刷画的油画 drawing:用硬笔画的素描/线条画 picture:真实形象所反映的画,如照片等,如take picture image:由印象而来的画,遥感影像做image,因是经过传感器印象而来 figure:轮廓图的意思,某个侧面的轮廓,所以有figure out的说法 diagra
最短路径-Dijkstra(迪杰斯特拉)算法
最短路径-Dijkstra(迪杰斯特拉)算法 网图的最短路: 最短路径,是指两顶点之间经过的边上权值之和最小的路径,并且我们称路径的第一个顶点是源点,最后一个顶点是终点 Dijkstra(迪杰斯特拉)算法: 概况: 按路径长度递增的次序产生的最短路径算法,通过一步步计算出路径之间顶点的最短路径,在此过程中都是基于已经求出的最短路径基础上,求得更远顶点的最短路径 思想:
数据结构——迪杰斯特拉算法求最短路径
问题描述 将图以邻接矩阵或邻接表存储,实现Dijkstra算法。 算法设计 迪杰斯特拉算法: 1.假设用带权的邻接矩阵arc,来表示带权有向图,arc[i][j],表示弧<vi,vj>上的权值。若<vi,vj>不存在,则置arc[i][j]为无穷。 S为已找到从v出发的最短路径的终点的集合,它的初始状态为空集。那么,从v出发到图上其余各顶点可能达到的最短路径长度的初值为: D[j]=arc
【LeetCode周赛284T4】6032. 得到要求路径的最小带权子图【困难】图最短路径:迪杰斯特拉dijkstra
6032. 得到要求路径的最小带权子图 题目思路代码算法复杂度 题目来源于leetcode,解法和思路仅代表个人观点。传送门。 难度: 困难(T4) 时间:- 题目 给你一个整数 n ,它表示一个 带权有向 图的节点数,节点编号为 0 到 n - 1 。 同时给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi, weighti] ,表
数据结构课程设计(四):行车路线问题(C++、图、迪杰斯特拉算法、最短路径)
题目要求 小明和小芳出去乡村玩,小明负责开车,小芳来导航。 小芳将可能的道路分为大道和小道。大道比较好走,每走1公里小明会增加1的疲劳度。小道不好走,如果连续走小道,小明的疲劳值会快速增加,连续走s公里小明会增加s2的疲劳度。 例如:有5个路口,1号路口到2号路口为小道,2号路口到3号路口为小道,3号路口到4号路口为大道,4号路口到5号路口为小道,相邻路口之间的距离都是2公里。如果小明从
迪杰斯特拉(Dijkstra)算法求图中最短路径
迪杰斯特拉(Dijkstra )算法: 对于图G=(V,E),将图的顶点分为两组: 顶点集S:已求出的最短路径的顶点集合(初始为{v0}); 顶点集V-S:尚未求出最短路径的顶点集合(初始为V-{v0} )。 算法按最短路径长度的递增顺序逐个将V-S的顶点加入S中,直到所有顶点均被加入S为止。 算法需借助辅助数组dist[N], dist[i]表示目前已经找到的、从开始点v0到终
迪杰斯特拉最短路径算法
问题 A: 算法7-15:迪杰斯特拉最短路径算法 时间限制: 1 Sec 内存限制: 32 MB 题目描述 在带权有向图G中,给定一个源点v,求从v到G中的其余各顶点的最短路径问题,叫做单源点的最短路径问题。 在常用的单源点最短路径算法中,迪杰斯特拉算法是最为常用的一种,是一种按照路径长度递增的次序产生最短路径的算法。 可将迪杰斯特拉算法描述如下: 在本题中
迪杰斯特拉(Dijsktra)算法求到任意节点的最短路径
迪杰斯特拉算法要求 1.必须给一个起点,求出起点到任何节点的最短路径,如果不可达那么距离设定为正无穷 2.输出一张表记录一个节点到任何节点的最短路径 3.dijkstra本质是一种贪心算法 要求: 不能
数据结构——迪杰斯特拉算法求最短路径
问题描述 将图以邻接矩阵或邻接表存储,实现Dijkstra算法。 算法设计 迪杰斯特拉算法: 1.假设用带权的邻接矩阵arc,来表示带权有向图,arc[i][j],表示弧<vi,vj>上的权值。若<vi,vj>不存在,则置arc[i][j]为无穷。 S为已找到从v出发的最短路径的终点的集合,它的初始状态为空集。那么,从v出发到图上其余各顶点可能达到的最短路径长度的初值为: D[j]=arc
HDU 2544,最短路径算法(迪杰斯特拉算法)
HDU-2544,题目链接在这里 在每年的校赛里,所有进入决赛的同学都会获得一件很漂亮的t-shirt。但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候,却是非常累的!所以现在他们想要寻找最短的从商店到赛场的路线,你可以帮助他们吗? Input 输入包括多组数据。每组数据第一行是两个整数N、M(N<=100,M<=10000),N表示成都的大街上有几个路口,标号为1的路口是商店所在地
图的最短路径(迪杰斯特拉和Floyd)
<span style="font-family: Verdana, Arial, Helvetica, sans-serif; background-color: rgb(255, 255, 255);">Dijkstra算法</span> 1.定义概览 Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中
Dijkstra算法 | 迪杰斯特拉算法-迷宫解算器可视化
Dijkstra算法 该算法维护一组已访问的顶点和一组未访问的顶点。 它从源顶点开始,迭代地选择距源具有最小暂定距离的未访问顶点。 然后,它访问该顶点的邻居,如果找到更短的路径,则更新它们的暂定距离。 这个过程一直持续到到达目的地顶点,或者所有可到达的顶点都被访问过。 在许多应用中都需要 Dijkstra 算法,其中找到两点之间的最短路径至关重要。 例如,它可以用于计算机网络的路由协议,也可以
ccf 交通规划(迪杰斯特拉优先队列模板)
什么跟什么就是刘汝佳小白书迪杰斯特拉队列的优先队列法 #include<bits/stdc++.h>using namespace std;#define INF 0x3f3f3f3ftypedef pair<int,int> pii;vector<pair<int,int> >g[10010];bool vis[10010];int cost[10010];int dist[
Dijkstra(迪杰斯特拉)算法
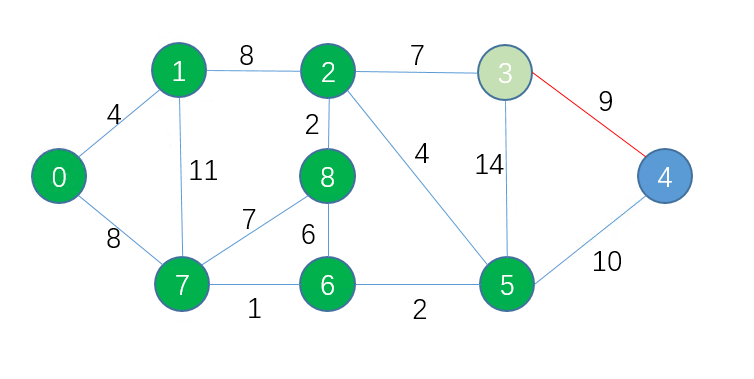
Dijkstra(迪杰斯特拉)算法的思想是广度优先搜索(BFS) 贪心策略。 是从一个顶点到其余各顶点的最短路径算法,节点边是不各自不同的权重,但都必须是正数 如果是负数,则需要 Bellman-Ford 算法 如果想求任意两点之间的距离,就需要用 Floyd 算法 求节点0 -> 4 的最短路径 每次从未标记的节点中选择距离出发点最近的节点,标记,收录到最优路径集合中计算刚加入节点A