本文主要是介绍最短路径问题——(弗洛伊德算法与迪杰斯特拉算法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最短路径问题——(弗洛伊德算法与迪杰斯特拉算法)【板子】
题目:
对于下面的图片所给出的关系,回答下面两个问题:
- 利用迪杰斯特拉算法求点A到每一个点之间的最小距离。
- 利用弗洛伊德算法求每两个点之间的最短路径。
(注意图中的A~E,分别用1~5来代替)
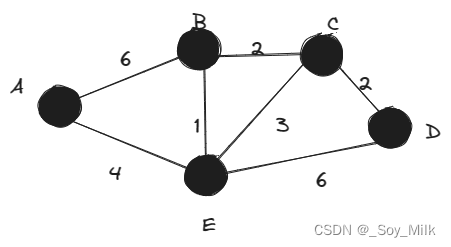
对于问题1(Dijkstra):
第一行输入三个数n,m,q分别表示一共有n个点,m条边,q个查询
接下来的m行每行输入三个数i,j,x,其中i,j分别表示边的起点和终点,x表示这条边的距离
最后q行,每行输入一个数字表示查询点A到每一个点之间的最短距离。
输入样例:
5 7 3 1 2 6 1 5 4 2 5 1 2 3 2 3 5 3 3 4 2 4 5 6输出样例:
5 7 4对于问题2(Floyd):
第一行输入三个数n,m,q分别表示一共有n个点,m条边,q个查询
接下来的m行每行输入三个数i,j,x,其中i,j分别表示边的起点和终点,x表示这条边的距离
最后q行,每行输入两个数字表示查询任意两个点之间的最短距离。
输入样例:
5 7 3 1 2 6 1 5 4 2 5 1 2 3 2 3 5 3 3 4 2 4 5 6 1 3 2 5 3 4输出样例:
7 1 2
问题1(Dijkstra):
// 最短路算法——迪杰斯特拉算法
#include<iostream>
#include<vector>
using namespace std;const int inf = 0x3f3f3f3f;
vector<int> dijkstra(vector<vector<int>> nums, int origin){int nsize = nums.size();vector<int> mk(nsize, 0); // 标记数组 vector<int> ans(nsize, inf);for(int i = 1;i < nsize;i ++) ans[i] = nums[i][origin];ans[origin] = 0; // 源点到源点的距离为0 mk[origin] = 1; // 对源点进行标记for(int i = 1;i < nsize - 1;i ++){// 首先找到没有标记的短路程的点int idx = 0; // ans[0] 的值是无穷大for(int i = 1;i < nsize;i++){if(!mk[i] && ans[i] < ans[idx]){idx = i;}}// 选出来之后进行标记 mk[idx] = 1;// 更新每一个举例for(int i = 1;i < nsize;i ++){if(ans[idx] + nums[idx][i] < ans[i]) ans[i] = ans[idx] + nums[idx][i];} }return ans;
}void solve(){// 使用int n;cin>>n; // 一共有n个点int m;cin>>m; // 一共有m条边 int q;cin>>q; // 一共有q个查询 vector<vector<int>> nums(n + 1, vector<int>(n + 1, inf));while(m--){int i,j,_x;cin>>i>>j>>_x;nums[i][j] = _x;nums[j][i] = _x;}vector<int> ans = dijkstra(nums, 1);// for(auto v : ans){
// cout<<v<<' ';
// }
// cout<<endl;// q次询问while(q--){int T;cin>>T;cout<<ans[T]<<endl;} return ;
}int main(){ios::sync_with_stdio(false);cin.tie(0);int t = 1;while(t--){solve();}return 0;
}
问题1(Floyd):
// 弗洛伊德算法
#include<iostream>
#include<vector>
using namespace std;
const int inf = 0x3f3f3f3f; vector<vector<int>> floyd(vector<vector<int>> nums){int nsize = nums.size();for(int k = 1;k < nsize;k++){ // 选择每一个点作为中间点进行更新 for(int i = 1;i < nsize;i ++){ for(int j = 1;j < nsize;j ++){if(nums[i][k] + nums[k][j] < nums[i][j]){nums[i][j] = nums[i][k] + nums[k][j];nums[j][i] = nums[i][j]; // 因为是无向边 }}}}return nums; }void solve(){// 使用int n;cin>>n; // 一共有n个点int m;cin>>m; // 一共有m条边 int q;cin>>q; // 一共有q个查询 vector<vector<int>> nums(n + 1, vector<int>(n + 1, inf));// 初始化自己到自己的距离为0for(unsigned i = 1;i < nums.size();i ++) nums[i][i] = 0; while(m--){int i,j,_x;cin>>i>>j>>_x;nums[i][j] = _x;nums[j][i] = _x;}vector<vector<int>> ans = floyd(nums);// for(auto v : ans){
// for(auto u : v){
// cout<<u<<' ';
// }
// cout<<endl;
// }
// cout<<endl;// q次询问while(q--){int i,j;cin>>i>>j;cout<<ans[i][j]<<endl;} return ;
}int main(){ios::sync_with_stdio(false);cin.tie(0);int t = 1;while(t--){solve();}return 0;
}
这篇关于最短路径问题——(弗洛伊德算法与迪杰斯特拉算法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





