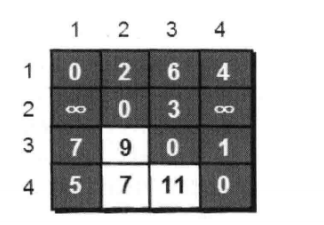
弗洛伊德专题
弗洛伊德(Floyd)算法(C/C++)
弗洛伊德算法(Floyd's algorithm),又称为弗洛伊德-沃尔什算法(Floyd-Warshall algorithm),是一种用于在加权图中找到所有顶点对之间最短路径的算法。这个算法适用于有向图和无向图,并且可以处理负权重边,但不能处理负权重循环。 弗洛伊德算法(Floyd-Warshall Algorithm)是一种用于计算图中所有顶点对之间最短路径的动态规划算法。本文将详细介绍弗
最短路径之弗洛伊德算法(Floyd)
Floyd算法又称为插点法,是一种用于寻找给定的加权图中多源点之间最短路径的算法。 路径矩阵 通过一个图的权值矩阵 求出它的每两点间的最短路径矩阵。 从图的带权邻接矩阵A=[a(i,j)] n×n开始,递归的进行n次更新,即由矩阵D(0)=A,按一个公式,构造出矩阵D(1); 又用同样地公式由D(1)构造出D(2);……;最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(
弗洛伊德算法——C语言
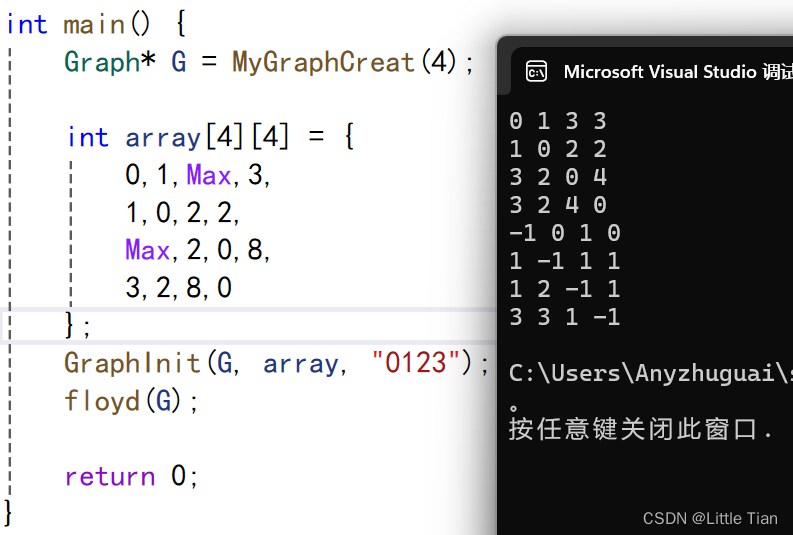
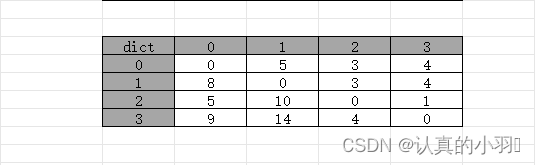
弗洛伊德算法,是一种用于解决所有顶点对之间最短路径问题的经典算法,该算法通过动态规划的方法计算出从每个顶点到其他所有顶点的最短路径。 弗洛伊德算法的基本思想是逐步考虑每一个顶点作为中间点,更新所有顶点对之间的最短路径。它通过以下三个步骤实现: 1.初始化距离二维数组,类似于这样: 2.加入中间节点,遍历每一对顶点,看距离是否减小。这里说明一下:以二维数组G->arc[i][j] 为例,G
多源最短路径算法 -- 弗洛伊德(Floyd)算法
1. 简介 Floyd算法,全名为Floyd-Warshall算法,亦称弗洛伊德算法或佛洛依德算法,是一种用于寻找给定加权图中所有顶点对之间的最短路径的算法。这种算法以1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德的名字命名。 2. 核心思想 通过考虑图中所有可能的中转点,逐步更新两点间的最短路径长度和路径信息,直至找到最终的最短路径。
弗洛伊德算法Floyed(求各顶点间最短路径):可打印最短路径
#include <iostream> #include <string> #include <iomanip> using namespace std; #define INFINITY 65535 #define MAX_VERTEX_NUM 10 typedef struct MGraph{ string vexs[10];//顶点信息 int arcs[10][10
最短路径问题——(弗洛伊德算法与迪杰斯特拉算法)
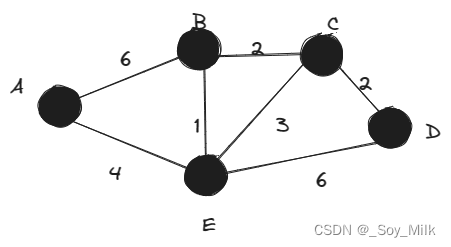
最短路径问题——(弗洛伊德算法与迪杰斯特拉算法)【板子】 题目: 对于下面的图片所给出的关系,回答下面两个问题: 利用迪杰斯特拉算法求点A到每一个点之间的最小距离。利用弗洛伊德算法求每两个点之间的最短路径。 (注意图中的A~E,分别用1~5来代替) 对于问题1(Dijkstra): 第一行输入三个数n,m,q分别表示一共有n个点,m条边,q个查询 接下来的m行每行输入三个数i,j,
弗洛伊德的经典精神分析理论,一文看懂潜意识
弗洛伊德认为人性本恶,对潜意识有深入研究。弗洛伊德是精神分析学的创始人,发表了《梦的解析》。精神分析的目的是把重要的无意识内容带入意识,并在意识中用理性的方式对其进行考察。 弗洛伊德理论是第一个综合性的人格理论,包括人格结构、人格动力、人格发展。 一、精神层次 早期,弗洛伊德把人格分成意识、前意识、潜意识。晚期,弗洛伊德把人格分成本我、自我、超我。 精神层次,也叫意识层次。精神层次包括
C#,图论与图算法,任意一对节点之间最短距离的弗洛伊德·沃肖尔(Floyd Warshall)算法与源程序
一、弗洛伊德·沃肖尔算法 Floyd-Warshall算法是图的最短路径算法。与Bellman-Ford算法或Dijkstra算法一样,它计算图中的最短路径。然而,Bellman Ford和Dijkstra都是单源最短路径算法。这意味着他们只计算来自单个源的最短路径。另一方面,Floyd Warshall计算输入图中每对顶点之间的最短距离。 假设你有5个朋友:比利、珍娜、卡西、艾
【备战蓝桥杯系列】多源最短路弗洛伊德floyd算法
floyd算法 蓝桥杯中,有时也会要求图中任意点的最短路径,这时候虽然可以用dijkstra,但是代码长,用floyd是最短的。模板如下。 模版 时间复杂度O(n^3) 使用邻接矩阵存储图 初始化:for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )if (i == j) d[i][j] = 0;else d[i][j]
最短路径-Floyd(弗洛伊德)算法
最短路径-Floyd(弗洛伊德)算法 简介: 相较Dijkstra,Floyd是一个完全穷举图中每个点到末尾点的最短路径 算法思想: 按惯例说两个工具 Path[MAX_SIZE][MAX_SIZE]:保存所有的最短路径(指向) Short_Path[MAX_SIZE][MAX_SIZE]:保存所有的最短路径长度(数组) 状态转移: Short_Path[v][w]
E题 弗洛伊德 迪克斯特拉模板题
E题 题目背景 巨噬细胞属免疫细胞,有多种功能,是研究细胞吞噬、细胞免疫和分子免疫学的重要对象。巨噬细胞容易获得,便于培养,并可进行纯化。巨噬细胞属不繁殖细胞群,在条件适宜下可生活2-3周,多用做原代培养,难以长期生存。 巨噬细胞是一种位于组织内的白血球,源自单核细胞,而单核细胞又来源于骨髓中的前体细胞。巨噬细胞和单核细胞皆为吞噬细胞,在脊椎动物体内参与非特异性防卫(先天性免疫)和特异性防卫(细
python 之弗洛伊德算法
文章目录 介绍代码蓝桥公园 介绍 弗洛伊德算法,也称为Floyd-Warshall算法,是一种用于解决图中所有节点对之间的最短路径问题的动态规划算法。它可以处理带有负权边但不含负权环的加权有向图或无向图。该算法以Robert Floyd和Stephen Warshall的名字命名,于1962年分别由他们独立提出。 以下是弗洛伊德算法的详细步骤: 初始化距离矩阵:创建一
最短路弗洛伊德算法。
题目 N M//接下来N行,每行X,Y,V。表示序号X到序号Y要V费。 X Y V .... X Y//最后一行表示要从序号X到Y; #include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace s
力扣-202. 快乐数解析-弗洛伊德循环查找算法
题目链接 public static void Happy(int n) {int sum = 0;int digit = 0;for (int i = 0; i < 20; i++) {while (n != 0) {digit = n%10;sum += digit*digit;n/=10;}System.out.print(sum + " ");n = sum;sum = 0;
Floyd(弗洛伊德)算法总结
知识概览 Floyd算法适合解决多源汇最短路问题,其中源点是起点,汇点是终点。时间复杂度是。 例题展示 题目链接 活动 - AcWing 系统讲解常用算法与数据结构,给出相应代码模板,并会布置、讲解相应的基础算法题目。https://www.acwing.com/problem/content/856/ 题解 Floyd算法基于动态规划的思想,主要是三重循环,先遍历k,i和
【数据结构】最短路径算法实现(Dijkstra(迪克斯特拉),FloydWarshall(弗洛伊德) )
文章目录 前言一、Dijkstra(迪克斯特拉)1.方法:2.代码实现 二、FloydWarshall(弗洛伊德)1.方法2.代码实现 完整源码 前言 最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。 单源最短路径问题:给定一个图G = ( V , E ) G=(V,E)G=(V,E),求源结点s ∈ V
数据结构课设-弗洛伊德算法C语言实现
我在大二上学期期末时候写的,大概2013年12月31号左右。我写在博客里一是为我以后复习所用,二是希望对需要的人有所帮助。 问题描述: 给出一张无向图,图上的每个顶点表示一个城市,顶点之间的边表示城市间存在的路径,边上的权值表示城市间的路径长度。利用弗洛伊德(Floyd)算法求解最短路径求解任意两个城市之间的最短路径问题。 #include<stdio.h> #include<stdl
Floyd算法(弗洛伊德)基本实现以及代码
文章目录 一、本文的由来二、简单介绍弗洛伊德和迪杰斯特拉的渊源三、算法思想1、文字解释2、图示解释 四、算法代码五、视频链接 一、本文的由来 数据结构老师布置了一个题目,要求我们写Floyd算法的实现过程的PPT(我不理解,孩子又不是教技的娃娃,为啥还要讲课做PPT嘞) 好吧~为了上课cue到我的时候,不会被发现我在摸鱼,我还是康了康视频,后面会把视频链接附在最后,有兴趣的同学可
【力扣热题100】287. 寻找重复数(弗洛伊德的乌龟和兔子方法)
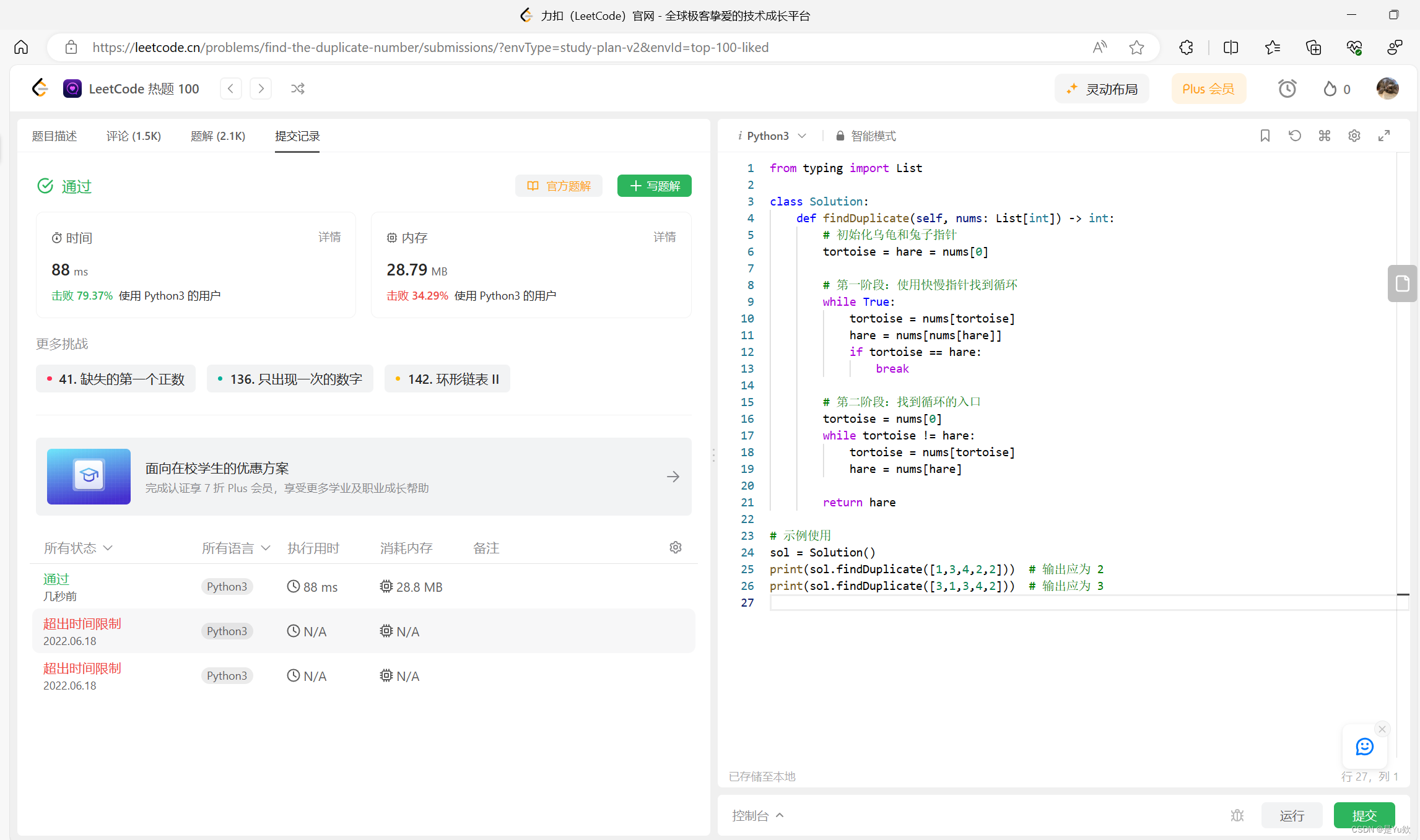
【力扣热题100】287. 寻找重复数 写在最前面理解解决 "寻找重复数" 问题的算法问题描述弗洛伊德的乌龟和兔子方法为什么这个方法有效? 代码复杂度 总结回顾 写在最前面 刷一道力扣热题100吧 难度中等 https://leetcode.cn/problems/find-the-duplicate-number/?envType=study-plan-v2&envId=to
最短路之——弗洛伊德算法(floyd)
来源: https://blog.csdn.net/riba2534/article/details/54562440 我们要做的是求出从某一点到达任意一点的最短距离,我们先用邻接矩阵来建图,map[i][j]表示从i点到j点的距离,把自己到自己设为0,把自己到不了的边初始化为无穷大,代码为: [cpp] view plain copy //初始化 for(i
数据结构上机实现——弗洛伊德算法
前言 它的思想就是在两个端点之间不断加入新节点,然后路径判断是否更短。同样,注释已经很详细了,原理不做深究,请自行复习。 注:本文的实验案例都是清华大学严蔚敏老师数据结构视频中所讲解的案例,所以本类的文章是十分适合大家对课上知识加深认识的。测试案例和源代码将会在文末给出。 算法 本算法的存储结构为邻接矩阵,类型声明如下: typedef struct _graph {int ma
最短路之Floyd(弗洛伊德)
只有五行的Floyd最短路算法: 核心代码 每次都更新通过k点,然后从i到j的最短路程。。。 转载于:https://www.cnblogs.com/ouyang_wsgwz/p/6653725.html
弗洛伊德算法三重循环的最通俗理解
我是标题党 首先本解释仅限无向图无负边权…直奔主题,我先上一段代码 //i是起点,j是终点,k是中转点for(int k = 1; k <= n; k++){for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){if(d[i][j] > d[i][k] + d[k][j]){d[i][j] = d[i][k] + d[k][j];}}