E题 弗洛伊德 迪克斯特拉模板题

E题
题目背景
巨噬细胞属免疫细胞，有多种功能，是研究细胞吞噬、细胞免疫和分子免疫学的重要对象。巨噬细胞容易获得，便于培养，并可进行纯化。巨噬细胞属不繁殖细胞群，在条件适宜下可生活2－3周，多用做原代培养，难以长期生存。

巨噬细胞是一种位于组织内的白血球，源自单核细胞，而单核细胞又来源于骨髓中的前体细胞。巨噬细胞和单核细胞皆为吞噬细胞，在脊椎动物体内参与非特异性防卫（先天性免疫）和特异性防卫（细胞免疫）。它们的主要功能是以固定细胞或游离细胞的形式对细胞残片及病原体进行噬菌作用（即吞噬以及消化），并激活淋巴球或其他免疫细胞，令其对病原体作出反应。

题目描述
巨噬细胞需要打扫身体里的病原体和细胞残片，现在身体中有n个房间（编号为1~N），巨噬细胞在其中编号为k的房间刚刚打扫结束。房间之间有一些道路供巨噬细胞移动，请问巨噬细胞到其他的细胞最少要经过多少个房间呢？

输入输出格式
输入格式：
输入包括两行，第一行为两个整数n,k,m，分别表示房间的个数、巨噬细胞所在的房间、以及道路的条数。

接下来m行每行包括三个整数x,y分别表示，分别表示每条道路的起点和终点。

输出格式：
输出包括一行，包括n个 空格隔开 的整数，分别表示到每一个房间最少路过的房间数，如果某个房间无法到达，那个房间对应位置输出-1
输入输出样例

输入样例#1： 
10 3 12
1 2
2 3
3 4
3 7
4 7
7 9
9 10
4 8
4 5
1 5
1 6
6 5
输出样例#1： 
1 0 0 0 1 2 0 1 1 2

说明
输出为要经过的房间的数量，不包括起点房间和终点房间，每条道路都是双向的。

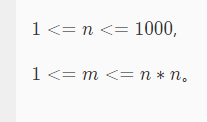
弗洛伊德，迪克斯特拉模板题，边权为1，下面给出迪克斯特拉的堆优化算法。

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f          //不加分号
using namespace std;const int maxn=1005;
int n,k,m;
int dis[maxn];
bool book[maxn];
int arr[maxn][maxn];void init()
{for(int i=0;i<maxn;++i)for(int j=0;j<maxn;++j)arr[i][j]=i==j?0:INF;    //数组初始化，i==j相当于自己到自己的距离，就0memset(dis,INF,sizeof(dis));memset(book,false,sizeof(book));
}int main()
{// freopen("test2.in", "r", stdin);// freopen("test2.out", "w", stdout);int x,y;cin>>n>>k>>m;init();          //调用函数初始化for(int i=0;i<m;++i){cin>>x>>y;arr[x][y]=arr[y][x]=1;   //记录}queue<int>q;        //队列，先进先出book[k]=true;dis[k]=0;    //使下边if循环中都满足第一次的循环q.push(k);while(!q.empty()){int now =q.front();q.pop();book[now]=false;for(int i=1;i<=n;++i){if(dis[i]>dis[now]+arr[now][i])                   //直走>中转{printf("dis[%d]=%d\n",i,dis[i]);                //测试printf("        dis[%d]=%d,arr[%d][%d]=%d\n",now,dis[now],now,i,arr[now][i]);//测试dis[i]=dis[now]+arr[now][i];printf("                 dis[%d]=%d\n",i,dis[i]);         //测试if(!book[i])        //只是最开始book[k]=false，这种情况下使用{book[i]=true;   //为了不重复走这个地方，所以最多更新n-1次就结束了q.push(i);       printf("         ..............................%d\n",i);        //测试}}}}//for(int i=1;i<=n;++i)//cout<<dis[i]<<"  "<<endl;for(int i=1;i<=n;++i)if(dis[i]>0)dis[i]--;     //问的是要经过的房间数，再-1呗for(int i=1;i<n;++i)       //先不到n，为了控制行末没有空格{if(dis[n]<INF)cout<<dis[i]<<" ";else cout<<-1<<" ";}cout<<(dis[n]<INF?dis[n]:-1)<<endl;return 0;
}

模板：

#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
const int maxn=1005;
int n,k,m;
int dis[maxn];
bool book[maxn];
int arr[maxn][maxn];
void init()
{for(int i=0;i<maxn;i++)for(int j=0;j<maxn;j++)arr[i][j]= i==j?0:INF;memset(dis,INF,sizeof(dis));memset(book,false,sizeof(book));
}
int main()
{int x,y;init();cin>>n>>k>>m;for(int i=0;i<m;i++){cin>>x>>y;arr[x][y]=arr[y][x]=1;}queue<int>q;book[k]=true;dis[k]=0;q.push(k);while(!q.empty()){int now=q.front();q.pop();book[now]=false;for(int i=1;i<=n;i++){if(dis[i]>dis[now]+arr[now][i]){dis[i]=dis[now]+arr[now][i];if(book[i]==false){book[i]=true;q.push(i);}}}}for(int i=1;i<=n;i++)if(dis[i]>0)dis[i]--;for(int i=1;i<n;i++){if(dis[i]<INF)printf("%d ",dis[i]);elseprintf("-1 ");}printf("%d",dis[n]<INF?dis[n]:-1);return 0;
}