迪克专题
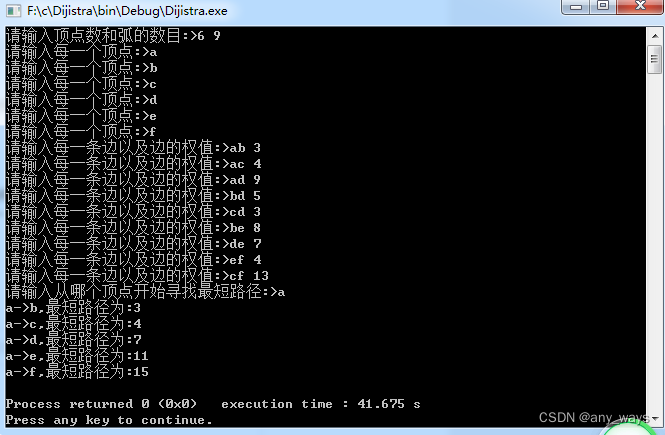
E题 弗洛伊德 迪克斯特拉模板题
E题 题目背景 巨噬细胞属免疫细胞,有多种功能,是研究细胞吞噬、细胞免疫和分子免疫学的重要对象。巨噬细胞容易获得,便于培养,并可进行纯化。巨噬细胞属不繁殖细胞群,在条件适宜下可生活2-3周,多用做原代培养,难以长期生存。 巨噬细胞是一种位于组织内的白血球,源自单核细胞,而单核细胞又来源于骨髓中的前体细胞。巨噬细胞和单核细胞皆为吞噬细胞,在脊椎动物体内参与非特异性防卫(先天性免疫)和特异性防卫(细
Dijkstra(迪克斯特拉)最短路径算法
1、算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 ,就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点
迪克斯特拉_迪克斯特拉错了,我也是
迪克斯特拉 我为使用基于0的数组而后悔,我错了。 让我与您分享为什么。 程序员应该使用索引符号 ,而不是偏移量符号。 偏移表示法是通过在连续内存的物理分配空间中从物理上分配的空间中的元素的对应位置来描述元素在数组中的位置的常用方法,该逻辑上从零开始。 否则它会缩短为“基于0的索引数组”,尽管它的误称实际上是偏移量。 我们应该改用1作为数组的开头,因为它具有以下优点: 自然,
数学建模--迪克斯特拉( Dijkstra)算法
先贴上迪克斯特拉算法的原理,该算法又称为PT标号法,对于算法的定义和步骤比较难以理解,只需要粗略看一下就好。Dijkstra’s Algorithm 基本思想: 若给定带权有向图G=(V,E)和源顶点v0,构筑一个源集合S,将v0加入其中。 ① 对差集V\S中 个顶点vi,逐一计算从v0 至它的距离 D(v0 , vi ),若该两顶点之间没有边,则其距离为无穷大。求出其中距离最短 的顶点w,将
迪克斯特拉 算法(算最短距离)
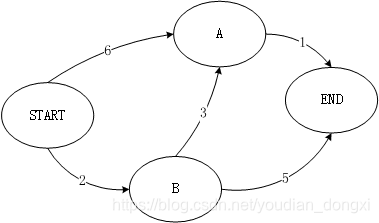
import timegraph = {}# 开始节点graph["start"] = {}graph["start"]["a"] = 6graph["start"]["b"] = 2# a节点graph["a"] = {}graph["a"]["fin"] = 1# b节点到下一节点的距离graph["b"] = {}graph["b"]["a"] = 3graph["b
图的最短路径之(迪克斯特拉)Dijkstra算法代码实现
一,Dijkstra算法 1,初始化:先找出从源V0到各终点Vk的直达路径(V0,Vk),即通过一条弧到达的路径.如果一条弧不能到达的点记为 无穷大 2,选择:从这些路径中找出一条长度最短的路径(V0,U). 3,更新:然后从其余各条路径进行适当调整: 若在图中存在弧(U,Vk),且(V0,U) + (U,Vk) < (V0,Vk),则以路径(V0,U,Vk)代替(V0,Vk) 4,在调
迪克斯特拉(Dijkstra)算法 单源最短路径
输入 第一行输入定点数N 第i行 s(起结点) k(与起结点相连的组数) g(终结点) v(权值) #include<stdio.h>#include<string.h>#define max 1000#define INF 999999int m[max][max]; //m[s][g]中记录s到g的边的权值int d[max]; //d[v]记录
【算法】迪克斯特拉算法之Java实现
迪克斯特拉算法是带权重的最短路径算法。 算法核心思想: 1. 找出当前距离起点距离最短的点。 2. 遍历该点的所有邻居节点,如果经过该点到邻居节点的距离比邻居原来的距离要更短,则更新邻居的距离。 3. 标记该点为已使用节点,寻找下一个未使用的且距离起点最近的节点。重复1,2操作。 4. 所有的节点都被标记后,最短路径就找到了! 举个例子: public static voi
将A*算法讲明白的大牛 感谢原作者Frank_chen 基础是迪克斯特拉算法
https://www.cnblogs.com/FrankChen831X/p/10358120.html https://www.cnblogs.com/csushl/p/10065069.html A* 算法详解 最近刷bin巨的搜索进阶专题,做到一个需要A*算法来解决的题,于是开始学A*算法,十分有用处的算法,虽然看上去听复杂的,但其实原理很容易理解,下面转自一篇文章,讲得真的很好。
【数据结构】最短路径算法实现(Dijkstra(迪克斯特拉),FloydWarshall(弗洛伊德) )
文章目录 前言一、Dijkstra(迪克斯特拉)1.方法:2.代码实现 二、FloydWarshall(弗洛伊德)1.方法2.代码实现 完整源码 前言 最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。 单源最短路径问题:给定一个图G = ( V , E ) G=(V,E)G=(V,E),求源结点s ∈ V