本文主要是介绍Python数据结构10:图,代码表示,DFS、BFS,拓朴排序,迪杰斯特拉,最小生成树,关键路径,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 定义
“图”这个字在中文当中,指代的是图画,但是在英文当中有很多种不同的涵义。
painting:用画刷画的油画
drawing:用硬笔画的素描/线条画
picture:真实形象所反映的画,如照片等,如take picture
image:由印象而来的画,遥感影像做image,因是经过传感器印象而来
figure:轮廓图的意思,某个侧面的轮廓,所以有figure out的说法
diagram:抽象的概念关系图,如电路图、海洋环流图、类层次图
chart:由数字统计来的柱状图、饼图、折线图
map:地图;plot:地图上的一小块
graph:重在由一些基本元素构造而来的图,如点、线段等
我们在数据结构中所说的图是指Graph,由节点和边构成。
图Graph是比树更为一般的结构,实际上树是一种具有特殊性质的图。
图包含:
- 顶点 Vertex: key 名称, payload 数据项
- 边 edge(弧 arc):
图的表示: G = (V, E)
- G 表示整个图
- V 是所有顶点的集合
- E 是所有边的集合
路径 Path:就是从一个顶点到另一个点所走过的路(包含路过的顶点)
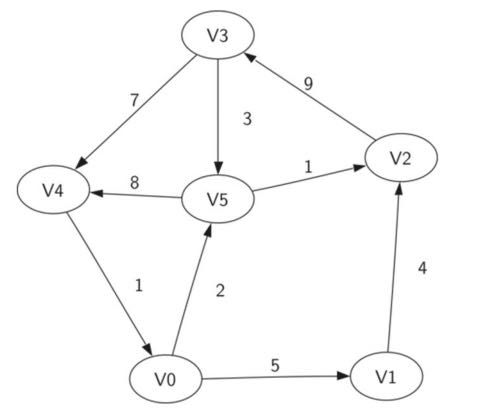
如在下图里 Path = (V3, V1, V2, V4)
意思就是从 V3到V4 路过 V1和V2
环 Cycle:第一个点和最后一个点相同的路径,绕着圈走就是环
如下图的Cycle = (V3, V5, V2, V3)
入度:指向这个节点的箭头的个数
出度:这个节点指向别的节点的个数
总度数: 入度和出度的和
如下图, V0的总度数是3, 入度是1,出度是2
V5 的总度数是 4,入度是2,出度也是2
连通:
- 顶点连通:一个顶点到另一个顶点有路径,他俩就是连通的
- 连通图:任意两个顶点都连通
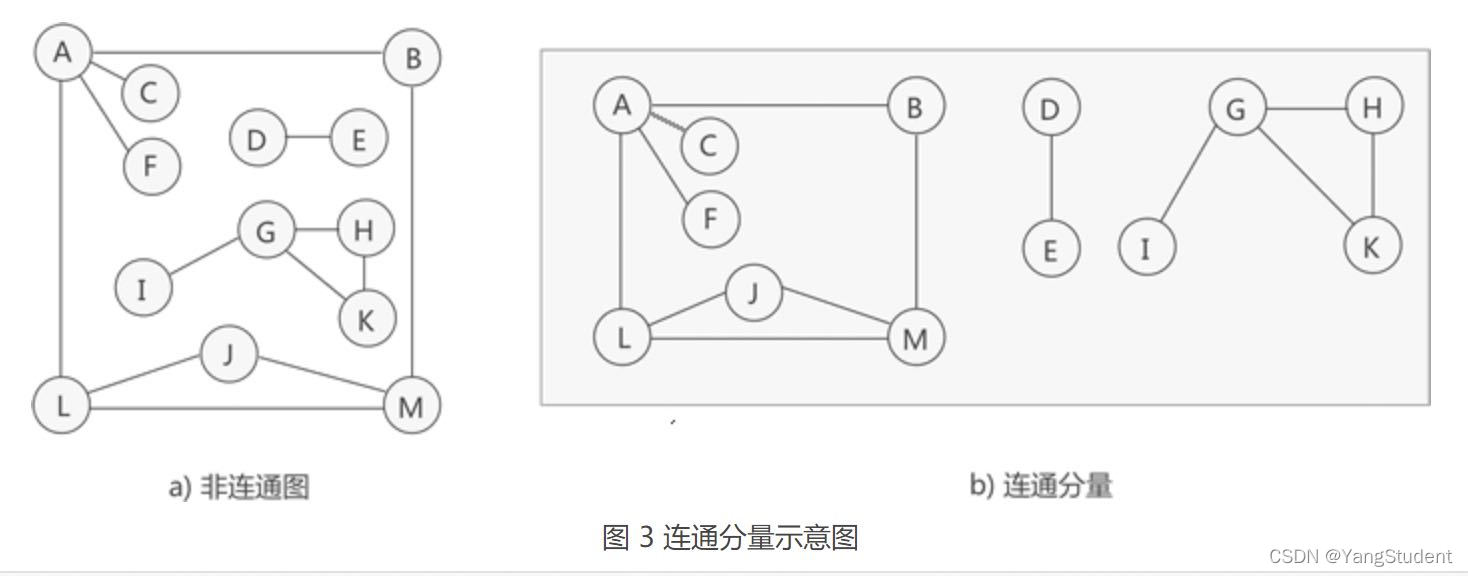
- 连通分量(极大连通子图):对于非连通图,他的一个子图是连通图且这个子图包含子图里面所有的顶点和边时,这个子图就是连通分量(极大连通子图)如下图所示
- 强连通图:强连通图必须是有向图,且当任意一对顶点Vi和Vj 都有 Vi -> Vj 和 Vj -> Vi都连通时,就是强连通图
- 强连通分量:非强连通图的有向图,其中的强连通子图,就是强连通分量
2. 图的数据结构表示方法
2.1 邻接矩阵 adjacency matrix
| V0 | V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|---|
| V0 | 5 | 2 | ||||
| V1 | 4 | |||||
| V2 | 9 | |||||
| V3 | 7 | 3 | ||||
| V4 | 1 | |||||
| V5 | 1 | 8 |
这个图的看法就是 V0 -> V1 = 5
优点:简单
缺点:矩阵里面有很多空出来的地方没写,导致矩阵太稀疏,浪费空间。
2.2 邻接表
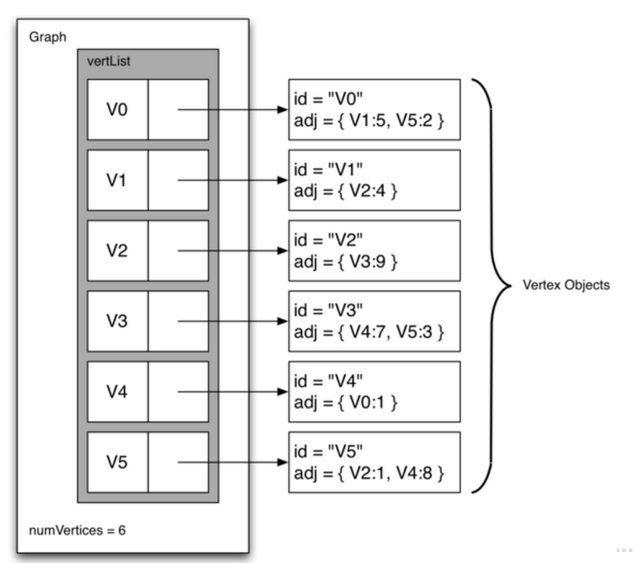
左边是主列表,先写明所有的顶点,右边列表中每个元素所包含的内容,id就是节点的名字,adj包含了此顶点的邻接节点和到达此节点的权重。
优点是紧凑高效
3. 图的遍历
3.1 深度优先搜索 DFS deep first search
从顶点出发,一直访问没访问过的当前顶点的邻接点,一轮遍历完后,如果还有没有访问过的顶点,就选他做新的顶点,再来一次遍历
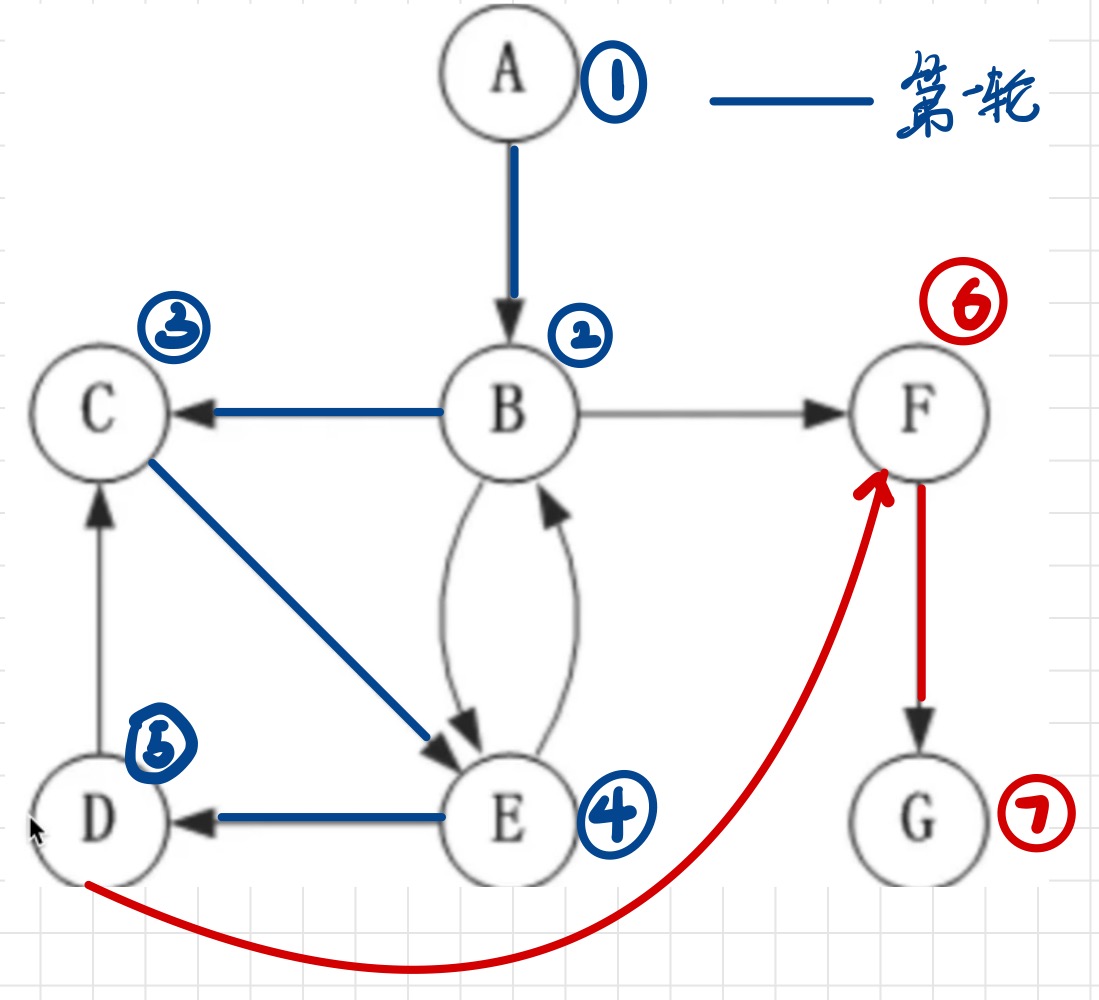
如这个图遍历的过程
A - B - C - E - D 所有的这条路上的邻接点都遍历完了
F 还没遍历过,选他开始再次遍历
F - G
最后的结果就是 A - B - C - E - D - F - G
3.2 广度优先搜索 BFS Breadth-First-Search
按层遍历,开始的顶点是第一层,开始顶点的所有子节点是第二层,第二层的所有子节点是第三层,. . .
先遍历完当前层的所有顶点,再遍历下一层
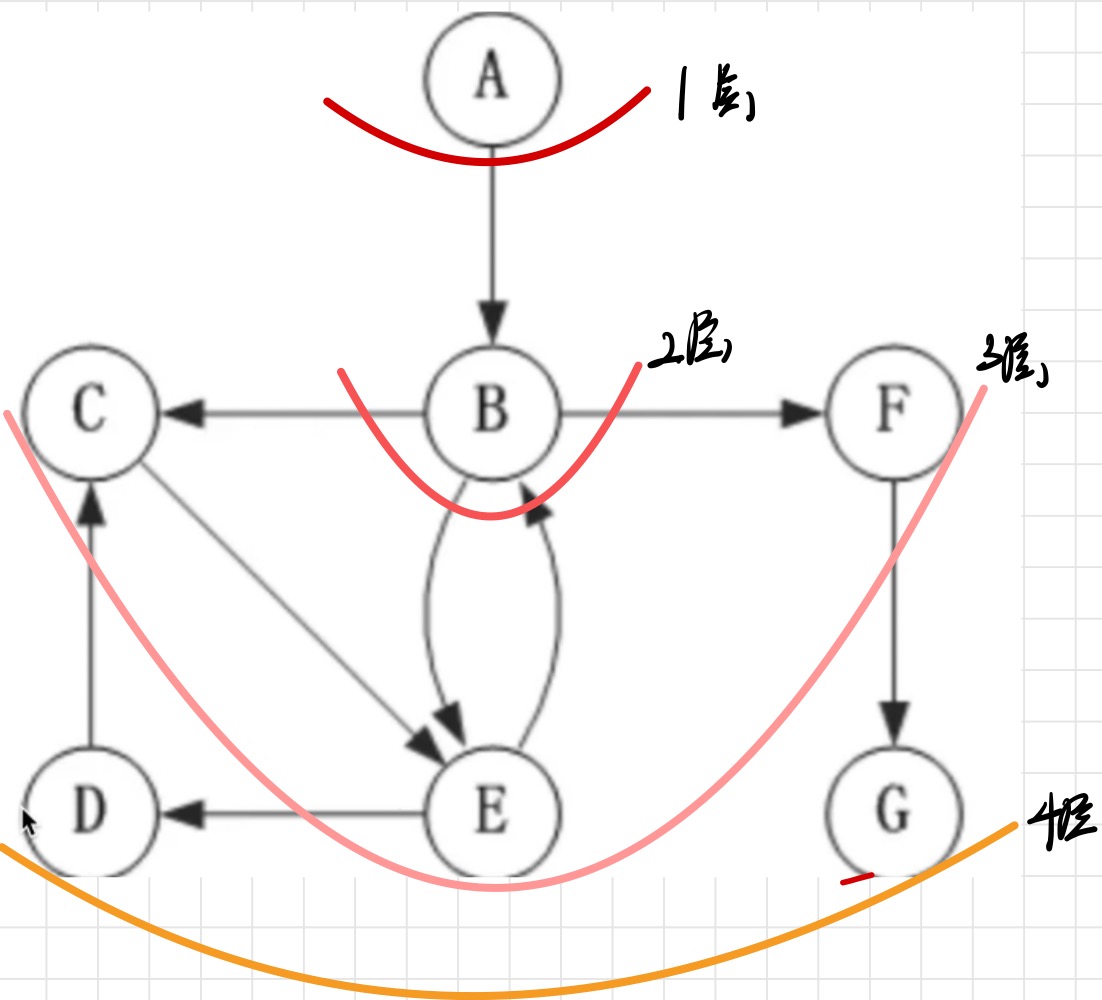
如这个图,A开始第一层,A的子节点B是第二层,B的子节点们CEF是第三层,第三层的E和F的子节点们DG是第四层。
A - B - C - E - F - D - G
4. 拓扑排序 Topological sort
这个视频讲的很好还简单
拓扑排序!(自讲)
简而言之,就是每次删除入度为0的顶点和它的边,作为所求序列的下一个值。
例如
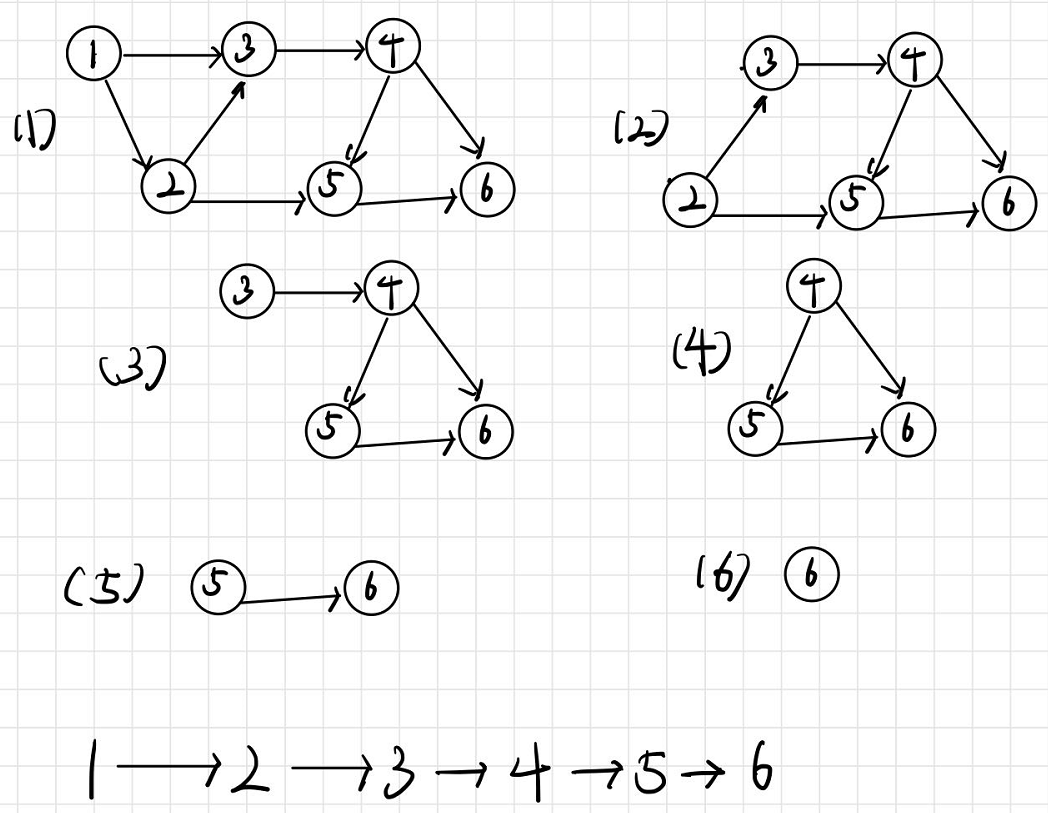
5. 迪杰斯特拉找最短路径
找图中任意一点到其他点最短路径。每次对所有可见点排序后,选距离最短的。
这个视频讲的很好还简单
【史上最清晰】手写迪杰斯特拉-Dijkstra(考试用)
例如
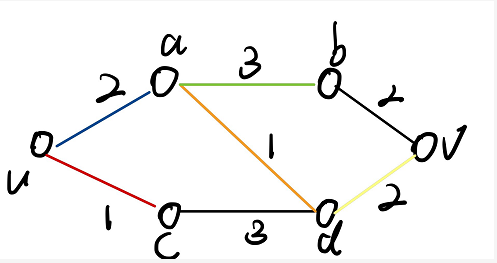
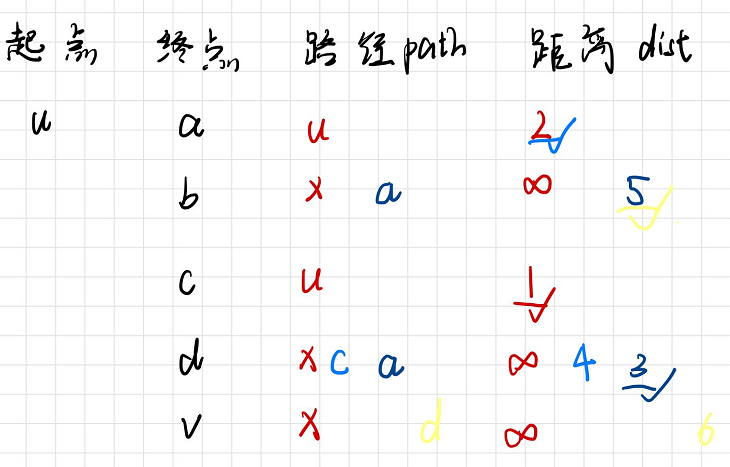
求解流程:
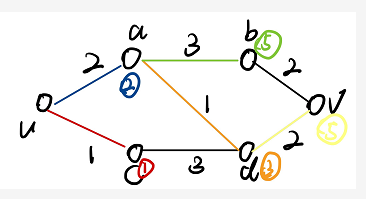
圈起来得数字是当前节点的起步代价,没圈起来的是顺序
画表格
6. 最小生成树:普利姆和克鲁斯卡尔
最小生成树实际上时最小代价生成树,就是一个图包含所有节点和尽可能少的边的子图,同时代价最小。有以下两种求法:
- Prim普利姆: 从顶点入手
1.随机选第一个顶点V1
2.找V1连着的代价的最小的边,此边另个节点设为V2
3.将 (V1, V2) 看作一个整体,继续找与这个整体相连(即,既可以与V1相连,也可以与V2相连)的最小代价的边,循环这个步骤,直到包含了所有的顶点
普利姆从顶点出发对稠密图更好用。
- Kruskal 克鲁斯卡尔
1.每次选权值最小的边,将顶点相连
克鲁斯卡尔从边出发,对稀疏图更好用
普利姆例子:
求这个图的最小生成树
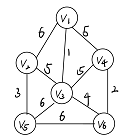
普利姆解法:
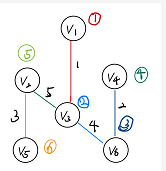
带圈的数字,是选定的顶点顺序
克鲁斯卡尔解法:
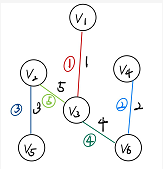
带圈的数字是选定的边的顺序
7. 找关键路径
关键路径就是在一个活动图中耗时最长的路径,耗时最长的路径上的活动都完成了,才能保证其他非关键路径的活动都完成。
这个up主讲的可以听懂,可以开2倍速,听起来顺畅一些
关键路径 例题讲解
例题:
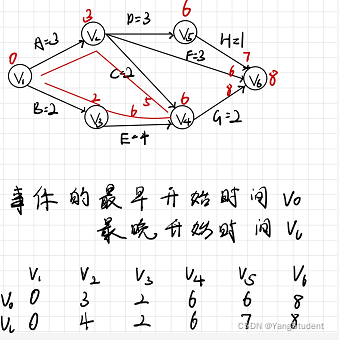

求这个图的关键路径。
顶点代表事件,边代表活动。
Vo :事件最早开始时间,先求这个。 从第一个顶点,从前往后求,每个顶点的最早开始时间都是路径的权值之和最大的那一条路径。
Vl :事件最晚开始事件,从最后一个顶点,往前减,每个顶点的最晚开始事件,是从后往前减最小的值。
e :活动最早开始时间,从前往后找最大的。
l :活动最晚开始时间,从后往前找最小的。
l-e:就是每个活动可以拖延的时间,等于0的表示不能拖延,是关键路径。
这篇关于Python数据结构10:图,代码表示,DFS、BFS,拓朴排序,迪杰斯特拉,最小生成树,关键路径的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





