本文主要是介绍js迪杰斯特拉算法求最短路径，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1.后台生成矩阵
名词解释和下图参考:https://blog.csdn.net/csdnxcn/article/details/80057574
double[,] arr = new double[allVertices.Count(), allVertices.Count()]; //矩阵
//allVertices所有三维坐标点的集合
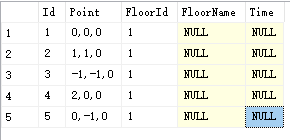
//lines 所有两点的连线
for (int i = 0; i < allVertices.Count(); i++)
{
for (int j = 0; j < allVertices.Count(); j++)
{
var start1 = allVertices[i].Point; //起点
var end1 = allVertices[j].Point; //终点
//lines 两点的连线集合
var line = lines.FirstOrDefault(ee => (ee.StartPoint == start1 && ee.EndPoint == end1)|| (ee.StartPoint == end1 && ee.EndPoint == start1/*起点终点互换*/));
if (start1 == end1)
{//同一个点
arr[i, j] = 0;
}
else
{
if (line != null)
{
arr[i, j] = double.Parse(line.Remark); //长度
}
else
{//两点未连接 此路不通
arr[i, j] =1.0/0.0; //Infinity
}
}
}
}
return arr;
2.dijkstra算法
/**
* Dijkstra算法
*
* @author wupanpan@baidu.com
* @date 2014-03-26
*/
/**
* @const
*/
var POS_INFINITY = Infinity;
/**
* @param {number} sourceV 源点的索引，从0开始
* @param {Array} adjMatrix 图的邻接矩阵，是一个二维数组
*/
function dijkstra(sourceV, adjMatrix) {
var set = [],
path = [],
dist = [];
distCopy = [],
vertexNum = adjMatrix.length;
var temp, u,
count = 0;
// 初始化
for (var i = 0; i < vertexNum; i++) {
distCopy[i] = dist[i] = POS_INFINITY;
set[i] = false;
}
distCopy[sourceV] = dist[sourceV] = 0;
while (count < vertexNum) {
u = distCopy.indexOf(Math.min.apply(Math, distCopy));
set[u] = true;
distCopy[u] = POS_INFINITY;
for (var i = 0; i < vertexNum; i++) {
if (!set[i] && ((temp = dist[u] + adjMatrix[u][i]) < dist[i])) {
distCopy[i] = dist[i] = temp;
path[i] = u;
}
}
count++;
}
return {
path: path,
dist: dist
};
}
/**
* @param {number} v 源点索引, 从0开始
* @param {number} d 非源点索引, 从0开始
* @param {Array} adjMatrix 图的邻接矩阵，是一个二维数组
*/
function searchPath(v, d, adjMatrix) {
var graph = dijkstra(v, adjMatrix),
path = graph.path,
dist = graph.dist;
var prev = path[d],
queue = [],
str = '';
queue.push(d);
while(prev != v) {
queue.push(prev);
prev = path[prev];
}
queue.push(v);
for (var j = queue.length - 1; j >= 0; j--) {
str +=queue.pop() + '->';
}
console.log('path',str);
var arr=str.split('->');
if(str.endsWith('->')){
arr.pop();
}
var rarr=[];//字符串数组转int数组
for(var i=0;i<arr.length;i++){
rarr.push(parseInt(arr[i]));
}
return rarr;
}
/**
* 测试数据
*/
var adjM = [
[0, 4, 2, POS_INFINITY, POS_INFINITY, POS_INFINITY],
[4, 0, 1, 5, POS_INFINITY, POS_INFINITY],
[2, 1, 0, 8, 10, POS_INFINITY],
[POS_INFINITY, 5, 8, 0, 2, 6],
[POS_INFINITY, POS_INFINITY, 10, 2, 0, 3],
[POS_INFINITY, POS_INFINITY, POS_INFINITY, 6, 3, 0]
];
3.使用算法求最短路径
5个点坐标如上图 虚线表示两点相连
1: 0,0,0
2: 1,1,0
3: -1,-1,0
4: 2,0,0
5: 0,-1,0
请求后台生成的矩阵为:
var pathMatrix = [
[
0,
1.73,
1.73,
"Infinity",
1
],
[
1.73,
0,
"Infinity",
1.73,
"Infinity"
],
[
1.73,
"Infinity",
0,
"Infinity",
"Infinity"
],
[
"Infinity",
1.73,
"Infinity",
0,
2.23
],
[
1,
"Infinity",
"Infinity",
2.23,
0
]
];
var ret = searchPath(4, 1, pathMatrix); //从第5点到第2点的最短路径
console.log('index', ret);
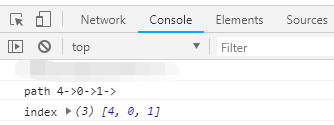(索引从0开始,对应到图上是 5->1->2)
4.使用threejs画出路径
(黑色连线; 红绿蓝为xyz辅助线)
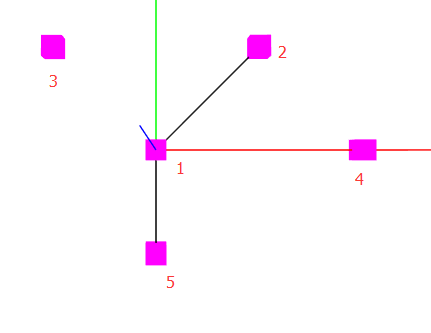
geometryPoint = new THREE.BoxGeometry(0.2, 0.2, 0.2);
var materialPoint = new THREE.MeshBasicMaterial({
color: 0xff00ff,
side: THREE.DoubleSide
});
circlePoint1 = new THREE.Mesh(geometryPoint, materialPoint);
circlePoint1.position.set(0, 0, 0);
scene.add(circlePoint1);
circlePoint2 = circlePoint1.clone();
circlePoint2.position.set(1, 1, 0);
scene.add(circlePoint2);
circlePoint3 = circlePoint1.clone();
circlePoint3.position.set(-1, 1, 0);
scene.add(circlePoint3);
circlePoint4 = circlePoint1.clone();
circlePoint4.position.set(2, 0, 0);
scene.add(circlePoint4);
circlePoint5 = circlePoint1.clone();
circlePoint5.position.set(0, -1, 0);
scene.add(circlePoint5);
scene.add(new THREE.AxesHelper(300));
//画路径
var ret = searchPath(4, 1, pathMatrix); //从第5点到第2点的最短路径
console.log('index', ret);
var geometry1 = new THREE.Geometry();
for (var i = 0; i < ret.length; i++) {
console.log("circlePoint" + (ret[i] + 1));
var pointObj = eval("circlePoint" + (ret[i] + 1));
console.log('position', pointObj.position);
geometry1.vertices.push(pointObj.position);
}
var line = new THREE.Line(geometry1, new THREE.LineBasicMaterial({
color: 'black'
}), THREE.LinePieces);
scene.add(line);
//补充
//threejs求三维两点的距离
var distance = circlePoint4.position.distanceTo(circlePoint5.position);
console.log(distance);
From:https://www.cnblogs.com/xuejianxiyang/p/9776319.html
这篇关于js迪杰斯特拉算法求最短路径的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
