算法笔记——图、图的定义方式、图的宽度优先遍历BFS、深度优先遍历DFS、拓朴排序算法、K算法、P算法、迪杰斯特拉算法

一、图的存储方式，如果表达图，生成图

1.图的存储方式

• 邻接表
  

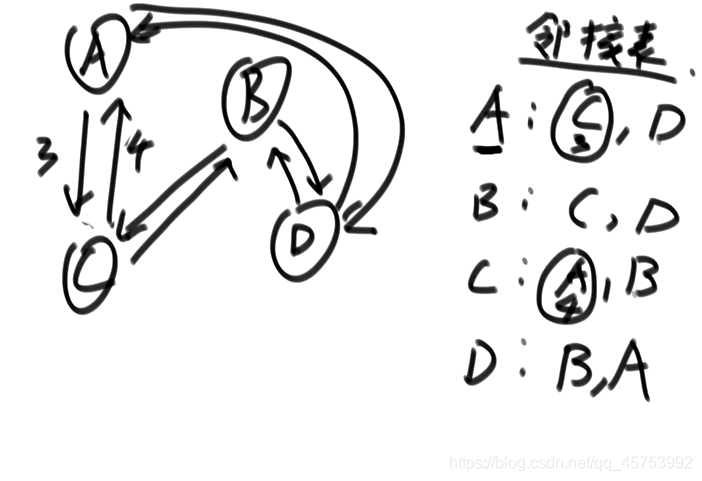
• 邻接矩阵
  

2.图的表达方式——点集、边集、图

• 点集

public class Node {public int value;public int in; //入度public int out; //出度public ArrayList<Node> nexts;  //由他发散的直接邻居的点public ArrayList<Edge> edges;  //属于我的边有哪些public Node(int value) {this.value = value;in = 0;out = 0;nexts = new ArrayList<>();edges = new ArrayList<>();}}

• 边集

public class Edge {public int weight; //权重public Node from;  //有向边frompublic Node to;  //有向边topublic Edge(int weight, Node from, Node to) {this.weight = weight;this.from = from;this.to = to;}}

• 图：点集+边集

public class Graph {public HashMap<Integer,Node> nodes; // 点集  这里的Integer代表出现的点的一个标记值public HashSet<Edge> edges;  //边集public Graph() {nodes = new HashMap<>();edges = new HashSet<>();}
}

3.生成图

• 二维数组，里面的每一个数组第一项表示权重，第二项表示from。第三项表示to

        public static Graph createGraph(Integer[][] matrix) {Graph graph = new Graph();//最外层循环表示进行几次大的循环，一次循环一个一维数组，一个边for (int i = 0; i < matrix.length; i++) {//每一个数组里面的第一个项表示权重Integer weight = matrix[i][0];//第二个项  表示from从哪里来Integer from = matrix[i][1];//第三个项  表示to指向哪里Integer to = matrix[i][2];//先判断这点有吗，没有加入，有的话就跳过//如果图的点集里还没有这个from点，把这个点加入这个点集//图的点集的更新if (!graph.nodes.containsKey(from)) {graph.nodes.put(from, new Node(from));//加入}//如果图的点集里还没有这个to点，把这个点加入这个点集if (!graph.nodes.containsKey(to)) {graph.nodes.put(to, new Node(to));//加入}//获取这个from点 和 to点Node fromNode = graph.nodes.get(from);Node toNode = graph.nodes.get(to);//通过这两个点和权重建立边Edge newEdge = new Edge(weight, fromNode, toNode);//接下来要更新：点、边、图该更新的都要更新//更新fromnode的点的nexts，也就是由他发散的直接邻居的点fromNode.nexts.add(toNode);//更新fromnode的点的out,也就是出度++fromNode.out++;//更新tonode的点的in,也就是入度++toNode.in++;//更新fromnode的edges，也就是更新属于fromnode的边，这是新增一个刚建立的边fromNode.edges.add(newEdge);//图更新，多加一个边集graph.edges.add(newEdge);}return graph;}

二、图的遍历

1.图的宽度优先遍历BFS

利用队列来实现
从源节点开始依次按照宽度进队列，然后弹出；
每弹出一个点，把该节点所有没有进过队列的邻接点放入队列；
直到队列边空。

//只需要点集那个类
public void BFS_(Node node){if(node == null){return;}//准备一个队列，用来依次按宽度弹出Queue<Node> queue = new LinkedList<>();//准备一个set集合，用来去重，防止一个节点重复被加入队列，最后重复输出这样的错误HashSet<Object> hashset = new HashSet<>();//先把源节点加入set和queuequeue.add(node);hashset.add(node);//如果队列不为空，依次弹出while(!queue.isEmpty()){Node cur = queue.poll();//弹出就输出System.out.println(cur.value);//每次弹出的时候，把弹出节点的所有相邻节点，还没有进过set的节点加入进行，并加到队列。for(Node next:cur.nexts){if(!hashset.contains(next)){hashset.add(next);queue.add(next);}}}
}

2.图的深度优先遍历DFS

深度优先遍历，从初始访问点出发，初始访问点可能有多个邻接结点，深度优先的遍历的策略是首先访问第一个邻接点，然后再以这个被访问的邻接结点作为初始访问结点，访问它的第一个邻接结点，即每一次访问完当前节点都会首先访问当前节点的第一个邻节点。类似迷宫回溯算法。
由此可见，当前的访问策略是优先往纵向挖掘深入，而不是对每一个节点的所有邻接点进行横向访问。

利用栈实现
一条独木桥走到黑
从源节点开始把每个结点按照深度放入栈，然后弹出；
每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈；
直到栈变空。

public void DFS_(Node head){HashSet<Node> hashset = new HashSet<>();Stack<Node> stack = new Stack<>();stack.push(node);hashset.add(node);System.out.println(node.value);while(!stack.isEmpty()){Node cur = stack.pop();for(Node next : cur.nexts){if(!hashset.contains(next)){//注意这里，要把cur本身也加进去，为什么，这样是给了后路，防止next遇到的都是已经在set中的，那就得找退路，也就是回溯，找别的节点了。stack.push(cur);stack.push(next);hashset.add(next);System.out.println(next.value);//break的原因就是让他不按照宽度，而是遇到一个就break这次的循环，让他接着新节点继续往下，如果不break那就去宽度了。break;}	}}	
}

三、拓朴排序算法

适用范围：要求有向图，且有入度为0的节点，且没有环
拓扑排序，其实就是寻找一个入度为0的顶点，该顶点是拓扑排序中的第一个顶点序列，将之标记删除，然后将与该顶点相邻接的顶点的入度减1，再继续寻找入度为0的顶点，直至所有的顶点都已经标记删除或者图中有环。
从上可以看出，关键是寻找入度为0的顶点。

依赖关系完成排序
有向图
利用哈希表
依次找到入度为0的点，依次擦掉，依次再找

	public static List<Node> sortTopology(Graph graph){//hashmap的K表示某一个node  V表示剩余的入度HashMap<Node, Integer> hashMap = new HashMap<>();//队列 剩余入度为0的点进入队列Queue<Node> zeroInQueue = new LinkedList<>();for (Node node : graph.nodes.values()){hashMap.put(node, node.in); // 记录原始入度if (node.in == 0){ // 第一批入度为0的点进队列zeroInQueue.add(node);}}//拓扑排序  结果放到resultList<Node> result = new ArrayList<>();while ( !zeroInQueue.isEmpty()){Node cur = zeroInQueue.poll();result.add(cur);//擦掉当前结点的影响for (Node next : cur.nexts){hashMap.put(next,hashMap.get(next) - 1); //入度被抹if (hashMap.get(next) == 0){zeroInQueue.add(next);}}}return result;}

四、最小生成树的两种算法

最小生成树===保证连通，权重最小，针对无向图

1.Kruskal算法

适用范围：要求无向图

• 算法概述

Kruskal算法可以简称为”加边法“。
1）总是从权值最小的边开始考虑，依次考察权值依次变大的边
2）当前的边要么进入最小生成树的集合，要么丢弃
3）如果当前的边进入最小生成树的集合中不会形成环，就要当前边
4）如果当前的边进入最小生成树的集合中会形成环，就不要当前边
5）考察完所有边之后，最小生成树的集合也得到了。

• 简述
  

1）对边排序，从最小的边出发，判断有无形成环（并查集），形成就不加，不形成就加
2）判断有无形成环，初始所有的点各自有一个集合，可以的话就合在一起。
3）集合查询和合并—>并查集或普通方法

• 普通方法

	public static class Mysets{public HashMap<Node, List<Node>> setMap;//点的集合的mappublic Mysets(List<Node> nodes){for (Node cur: nodes){List<Node> set = new ArrayList<>(); // 每个点的集合set.add(cur); //每个点的集合一开始是自己setMap.put(cur,set);}}//from和to在不在一个集合里public boolean isSameSet(Node from, Node to){List<Node> fromSet = setMap.get(from); //from的集合List<Node> toSet = setMap.get(to); //to的集合return fromSet == toSet; //判断是不是一个集合}//两个集合的合成public void union(Node from, Node to){List<Node> fromSet = setMap.get(from); //from的集合List<Node> toSet = setMap.get(to); //to的集合for (Node toNode : toSet){fromSet.add(toNode);setMap.put(toNode,fromSet);}}}//K算法public static Set<Edge> kruskalMST(Graph graph){Mysets mysets = new Mysets((List<Node>) graph.nodes.values());//优先级队列 底层是堆PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new Comparator<Edge>() {@Overridepublic int compare(Edge o1, Edge o2) {return o1.weight - o2.weight;}});for (Edge edge : graph.edges){priorityQueue.add(edge);}Set<Edge> result = new HashSet<>();while ( !priorityQueue.isEmpty()){Edge edge = priorityQueue.poll();if ( !mysets.isSameSet(edge.from, edge.to)){result.add(edge);mysets.union(edge.from, edge.to);}}return result;}

• 利用并查集

// Union-Find Setpublic static class UnionFind {private HashMap<Node, Node> fatherMap;private HashMap<Node, Integer> rankMap;public UnionFind() {fatherMap = new HashMap<Node, Node>();rankMap = new HashMap<Node, Integer>();}private Node findFather(Node n) {Node father = fatherMap.get(n);if (father != n) {father = findFather(father);}fatherMap.put(n, father);return father;}public void makeSets(Collection<Node> nodes) {fatherMap.clear();rankMap.clear();for (Node node : nodes) {fatherMap.put(node, node);rankMap.put(node, 1);}}public boolean isSameSet(Node a, Node b) {return findFather(a) == findFather(b);}public void union(Node a, Node b) {if (a == null || b == null) {return;}Node aFather = findFather(a);Node bFather = findFather(b);if (aFather != bFather) {int aFrank = rankMap.get(aFather);int bFrank = rankMap.get(bFather);if (aFrank <= bFrank) {fatherMap.put(aFather, bFather);rankMap.put(bFather, aFrank + bFrank);} else {fatherMap.put(bFather, aFather);rankMap.put(aFather, aFrank + bFrank);}}}}public static class EdgeComparator implements Comparator<Edge> {@Overridepublic int compare(Edge o1, Edge o2) {return o1.weight - o2.weight;}}public static Set<Edge> kruskalMST(Graph graph) {UnionFind unionFind = new UnionFind();unionFind.makeSets(graph.nodes.values());PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());for (Edge edge : graph.edges) {priorityQueue.add(edge);}Set<Edge> result = new HashSet<>();while (!priorityQueue.isEmpty()) {Edge edge = priorityQueue.poll();if (!unionFind.isSameSet(edge.from, edge.to)) {result.add(edge);unionFind.union(edge.from, edge.to);}}return result;}

2.Prim算法

适用范围：要求无向图
从点开始，找最小边，从而得到点，周而复始

public static class EdgeComparator implements Comparator<Edge>{@Overridepublic int compare(Edge o1, Edge o2) {return o1.weight - o2.weight;}}public static Set<Edge> primSet(Graph graph){//解锁的边进入小根堆PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());HashSet<Node> set = new HashSet<>(); //解锁过的点放在set里Set<Edge> result = new HashSet<>(); //依次挑选的边放入result//for循环处理森林问题 各自生成最小生成树 这是个特殊情况，如果整个是连通图，这里没必要加        for (Node node : graph.nodes.values()){//随便挑一个点//node是开始点if ( !set.contains(node)){set.add(node);for (Edge edge : node.edgs){ //由一个点，解锁所有相连的边priorityQueue.add(edge);}while ( !priorityQueue.isEmpty()){Edge edge = priorityQueue.poll(); //弹出解锁的边中，最小的边Node toNode = edge.to;//判断toNode是不是一个新的点，在不在set中if ( !set.contains(toNode)){ //不在，就是新点，就加入set.add(toNode);//要这个边result.add(edge);//toNode发散出去的边放入优先级队列for (Edge nextEdge : toNode.edgs){priorityQueue.add(nextEdge);}}}}}return result;}

五、Dijkstra算法

适用范围：没有权值为负数的边