【QuikGraph】C#调用第三方库实现迪杰斯特拉(Dijkstra)算法功能

本文主要是介绍【QuikGraph】C#调用第三方库实现迪杰斯特拉(Dijkstra)算法功能，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

QuikGraph库介绍

项目地址：https://github.com/KeRNeLith/QuikGraph
API地址：https://kernelith.github.io/QuikGraph/api/index.html

QuikGraph为.NET提供了通用的有向/无向图数据结构和算法。
QuikGraph提供了深度优先搜索、广度优先搜索、A*搜索、最短路径、k最短路径，最大流量、最小生成树等算法。

QuikGraph最初由Jonathan “Peli” de Halleux于2003年创建，并命名为QuickGraph。随后更新为YC.QuickGraph。

这个版本的QuickGraph，改名为QuikGraph，是YC.QuickGraph的一个分支。我尝试使用现代C#开发（.NET Core）清理该库，将其作为一个干净的NuGet包提供。该计划旨在全面清理、修复原始库及其所有非核心部件的问题，并对其进行改进。

示例

1. 创建一个.Net Framework4.7.2框架的项目。
2. 在NuGet上搜索QuikGraph，并安装。
3. 引入命名空间：

using QuikGraph.Algorithms.Observers;
using QuikGraph.Algorithms.ShortestPath;
using QuikGraph;

4. 主要测试代码：

        public void DijkstraSimpleGraph(){// 创建邻接图，使用string类型作为顶点、边的唯一标识var graph = new AdjacencyGraph<string, Edge<string>>(true);// 添加顶点到图中graph.AddVertex("A");graph.AddVertex("B");graph.AddVertex("D");graph.AddVertex("C");graph.AddVertex("E");// 创建边var a_b = new Edge<string>("A", "B");var a_c = new Edge<string>("A", "C");var b_c = new Edge<string>("B", "C");var b_e = new Edge<string>("B", "E");var c_d = new Edge<string>("C", "D");var d_e = new Edge<string>("D", "E");var e_d = new Edge<string>("E", "D");// 添加边到图中graph.AddEdge(a_b);graph.AddEdge(a_c);graph.AddEdge(b_c);graph.AddEdge(c_d);graph.AddEdge(d_e);graph.AddEdge(b_e);graph.AddEdge(e_d);// 定义边的权重var weight = new Dictionary<Edge<string>, double>(graph.EdgeCount){[a_b] = 30,[a_c] = 15,[b_c] = 10,[b_e] = 20,[c_d] = 40,[d_e] = 4,[e_d] = 2,};// 创建算法，传入图和权重var algorithm = new DijkstraShortestPathAlgorithm<string, Edge<string>>(graph, e => weight[e]);// Attach a Vertex Predecessor Recorder Observer to give us the paths// 使用顶点前置记录器，以提供路径计算var predecessorObserver = new VertexPredecessorRecorderObserver<string, Edge<string>>();using (predecessorObserver.Attach(algorithm))//以顶点A为起点，运行算法algorithm.Compute("A");//打印A为起点，到各个点的距离foreach (var vertex in graph.Vertices){Trace.WriteLine($"A-{vertex} = {algorithm.GetDistance(vertex)}");}}

打印输出结果（打印了A为起点，到各个顶点的距离）：

A-A = 0
A-B = 30
A-D = 52
A-C = 15
A-E = 50

图结构示意（可以人工检查输出结构的正确性）：

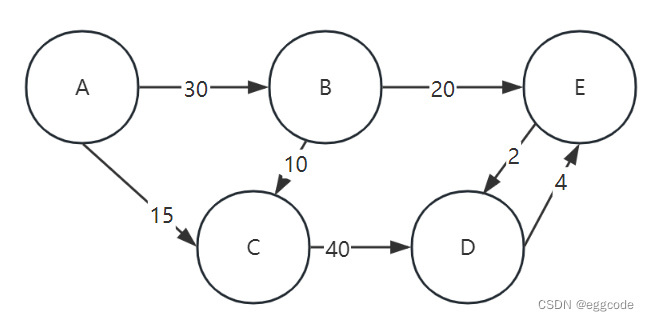
这篇关于【QuikGraph】C#调用第三方库实现迪杰斯特拉(Dijkstra)算法功能的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---