观测器专题
带衰减因子的积分磁链观测器
带衰减因子的积分磁链观测器 文章目录 带衰减因子的积分磁链观测器1. 背景问题2. 带衰减因子的积分器3. 理解公式4. 实现带衰减因子的积分器5. C语言代码实现6. 代码解释7. 带衰减因子的积分器的优点8. 实际应用中的考虑9. 总结 带衰减因子的积分器(also known as a Low-pass Filtered Integrator)是在电机控制中对磁链观测器进
永磁同步电机高性能控制算法(13)后续篇—— 基于高阶扩张状态观测器(ESO)的无模型预测控制(MFPC)
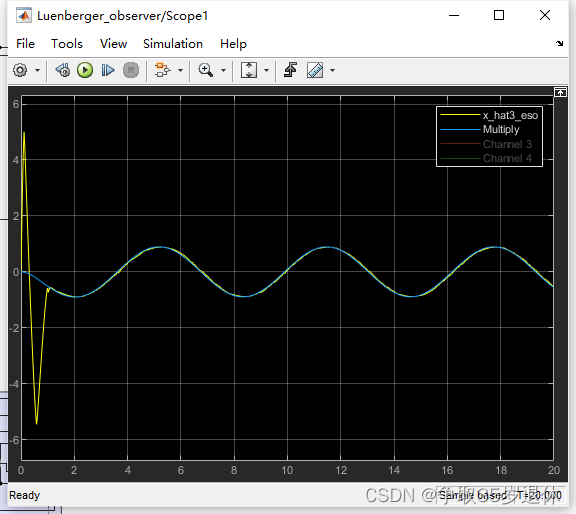
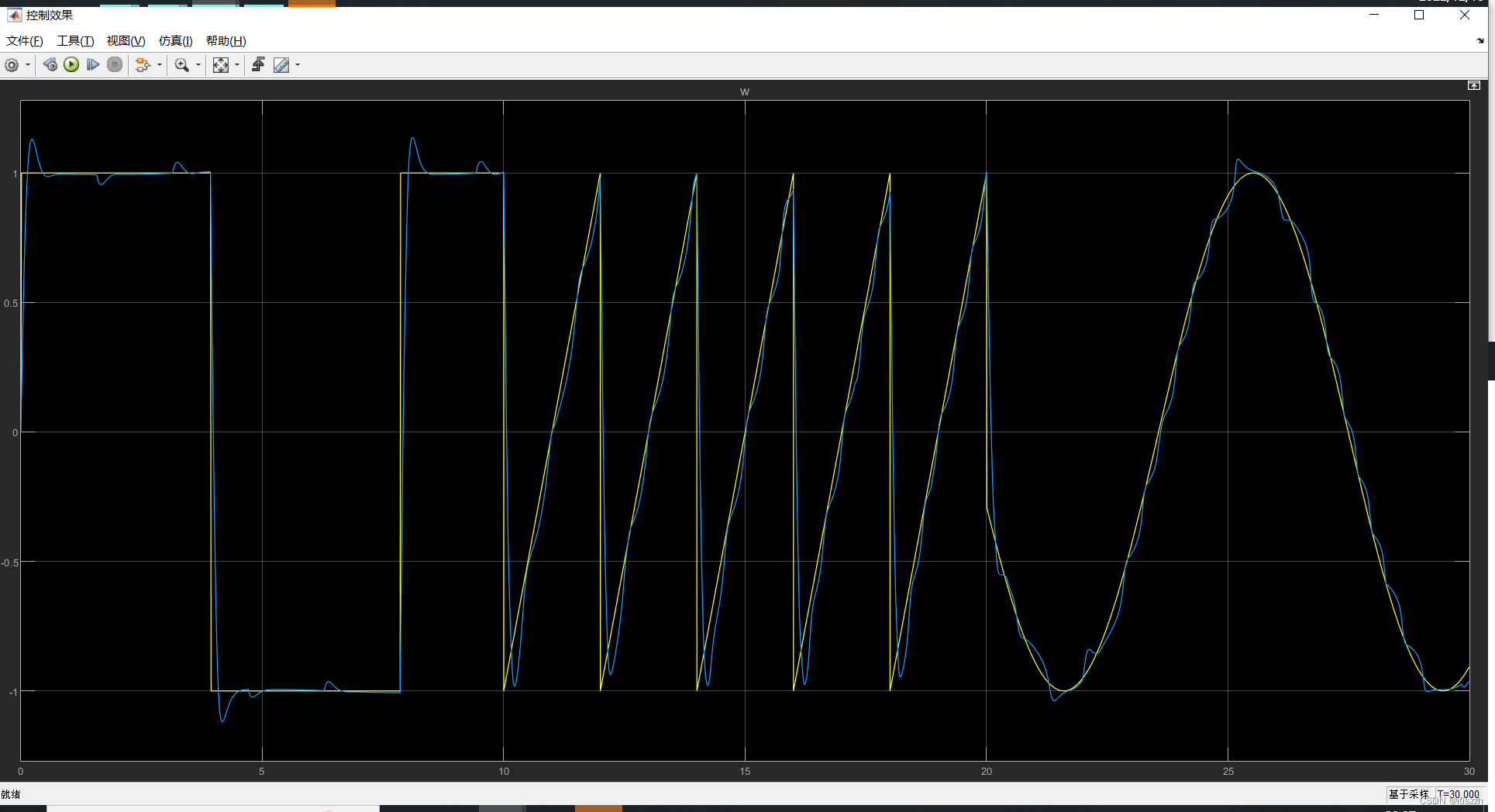
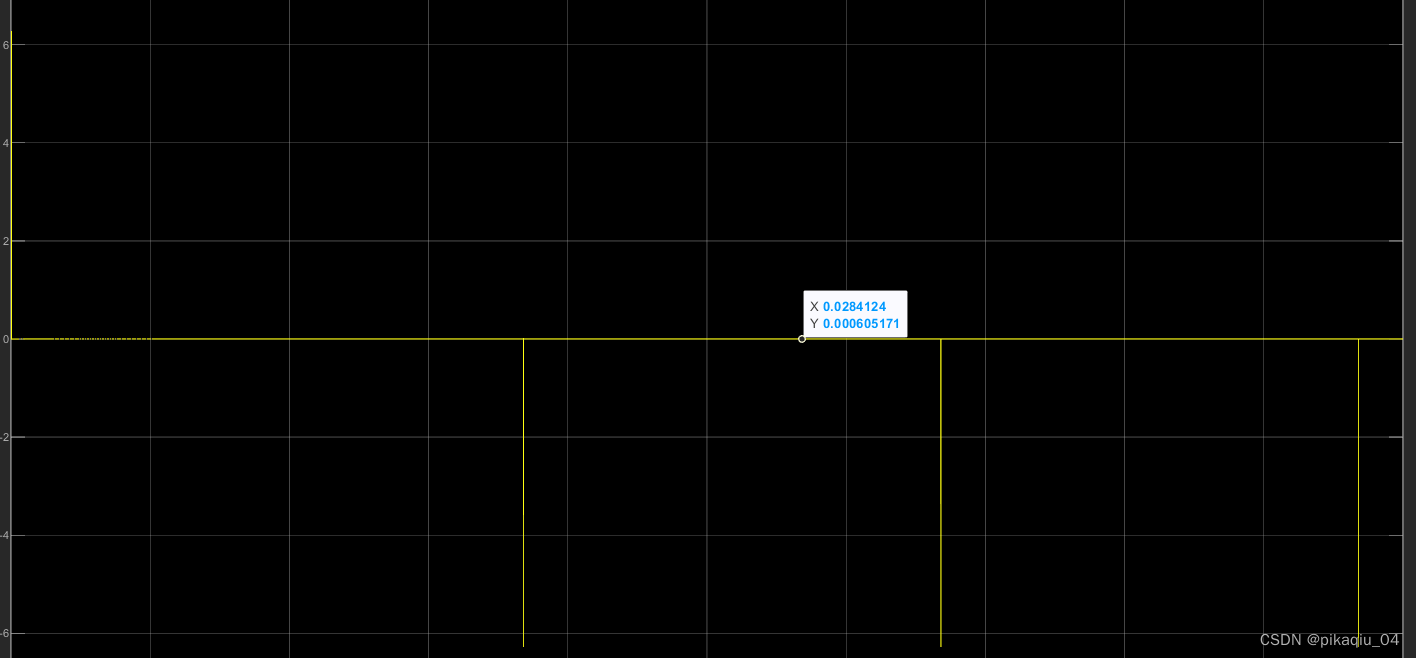
1.前言 前文已经介绍过了高阶ESO相对于传统ESO的优势。 https://zhuanlan.zhihu.com/p/703039702https://zhuanlan.zhihu.com/p/703039702 但是当时搭的ESO有点问题。把公式修正之后,发现前文用的改进四阶ESO无法使用。 今天来解释一下为什么改进4阶ESO无法使用。 2.为什么改进4阶ESO用不了? %扩展观测
电机控制系列模块解析(18)—— 位置观测器
一、简要综述 无传感器控制策略中观测器的分类,主要分为两类:基于模型的方法(Model Based)和基于显著性的方法(Saliency Based)。在此借用一张文献综述的图片,下面将列出下面借用图片中的各个分支的优缺点: 1. Model Based: 反电动势(Back-EMF): 优点:不需要PM磁链信息;不需要积分;在中高速下性能良好。缺点:在低速下性能较差;对电机参数变化敏感。
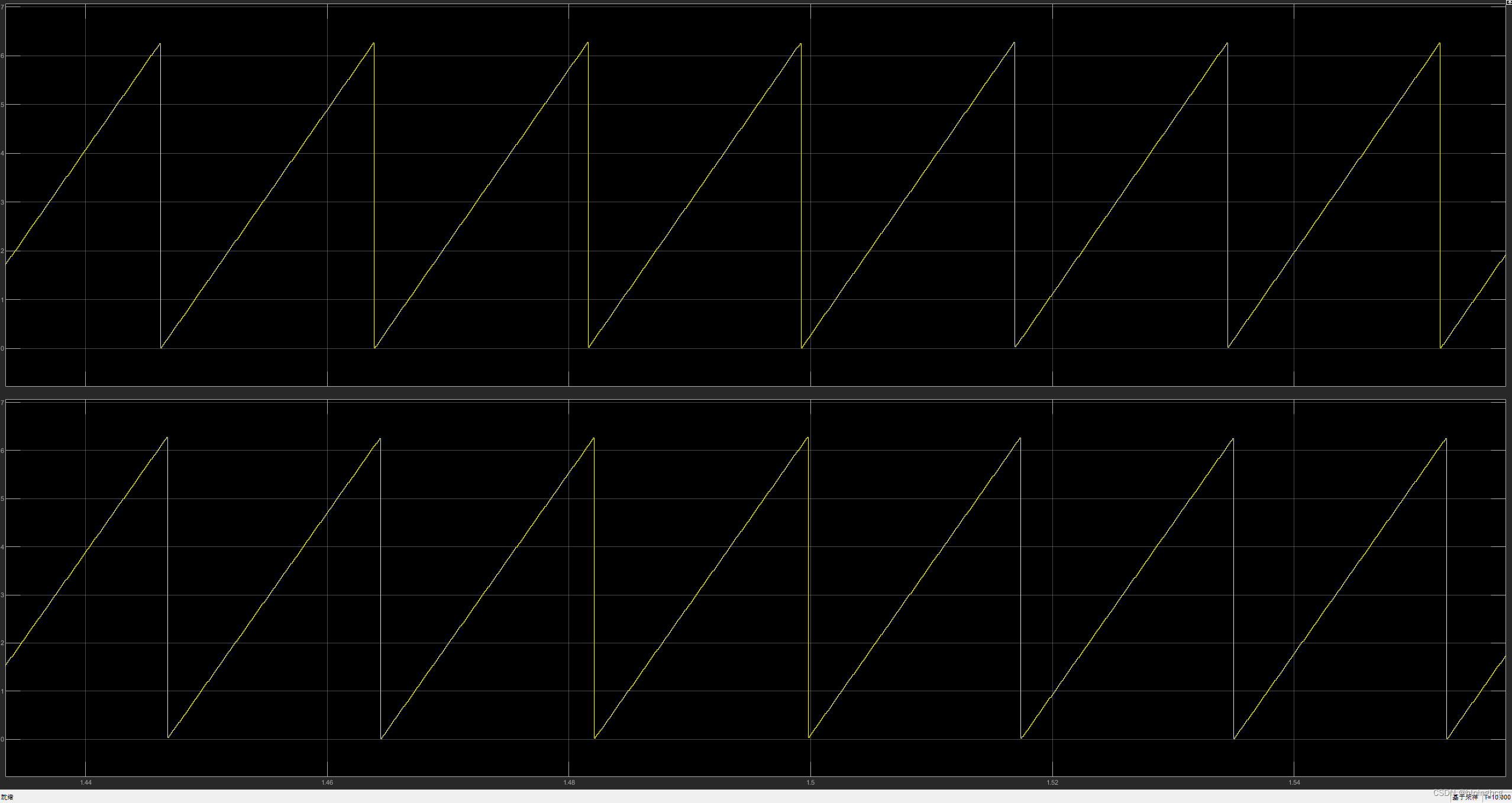
【电机控制】滑模观测器PMSM无感控制波形图
【电机控制】滑模观测器PMSM无感控制波形图 文章目录 前言一、FOC控制1.三相电流2.Clark变换静止坐标系iαiβ3.park变换旋转坐标系idiq4.电流环PI控制输出UdUq5.UdUq 反park变换UαUβ 二、反电动势观测器BEMF1.静止坐标系iαiβ提取反电动势EaEb2.反电动势EaEb提取位置信息、EqEd3.位置信息提取机械转速wr 总结
学习下控制 LQR加上观测器
这里主要参考B站上的,DR_CAN,极力推荐看下,这里主要是结合观测器和LQR的设计。在观测器基础上引入LQR 这里的Y的C=[1 0],可知X1输出是可以用实际值的,可以不用的X1hat
永磁同步电机无感FOC(龙伯格观测器)算法技术总结-实战篇
文章目录 1、ST龙伯格算法分析(定点数)1.1 符号说明1.2 最大感应电动势计算1.3 系数计算1.4 龙伯格观测器计算1.5 锁相环计算1.6 观测器增益计算1.7 锁相环PI计算(ST)1.8 平均速度的用意 2、启动策略2.1 V/F压频比控制2.2 I/F压频比控制 3、算法开发3.1 Luenberger核心算法模块3.1.1 Luenberger.h3.1.2 Luenber
永磁同步电机无感FOC(龙伯格观测器)算法技术总结-仿真篇
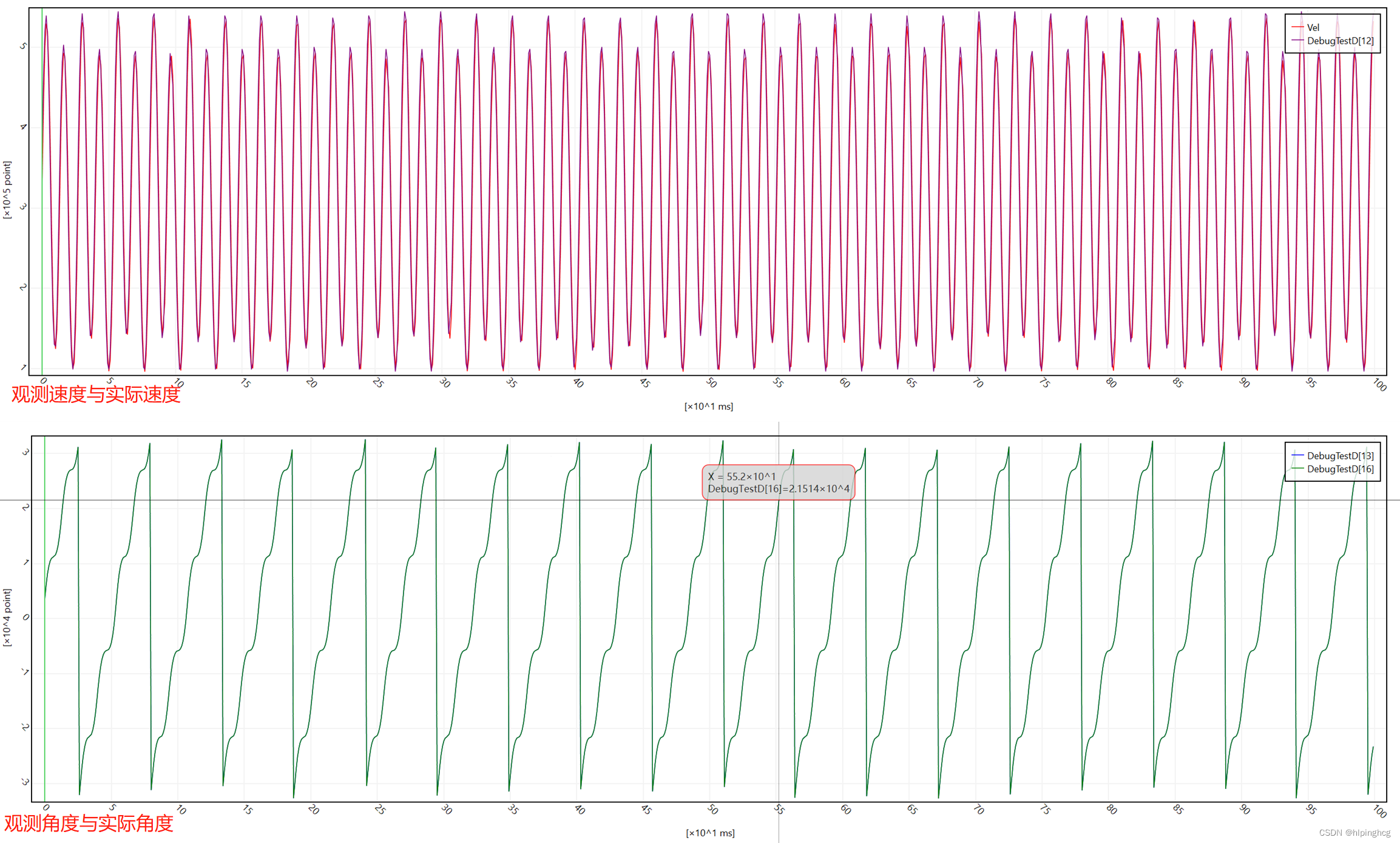
文章目录 1、观测器的引入2、β轴向下的电机观测器数学模型3、β轴向下的转子点角度及速度观测4、Simulink仿真模型搭建4.1模型总览4.2 Luenberger观测器模块4.2.1 I_alpha观测4.2.2 I_beta观测4.2.3 e_alpha、e_beta观测4.2.4 锁相环 4.3 速度设定4.4 速度观测结果4.5 电角度观测结果 模型下载地址:无感FOC
【电机仿真】HFI算法脉振高频电压信号注入观测器-PMSM无感FOC控制
【电机仿真】HFI算法脉振高频电压信号注入观测器-PMSM无感FOC控制 文章目录 前言一、脉振高频电压注入法简介(注入在旋转坐标系的d轴)1.旋转高频电压(电流)注入法2.脉振高频电压注入法 二、高频注入理论1.永磁同步电机的高频模型2.估计坐标系3.上式联立得到4.在估计的两相旋转坐标系的直轴上注入高频余弦电压信号5.将4代入3可得6.PI调节器的输入量计算7.脉振高频电压注入法
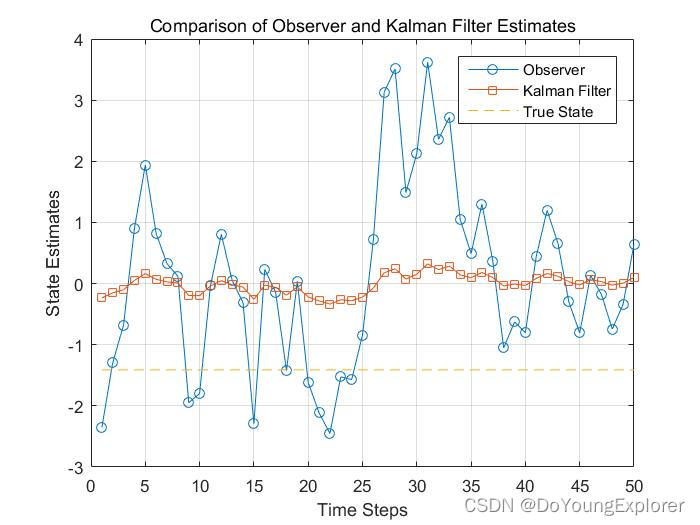
观测器与卡尔曼滤波器的状态估计对比
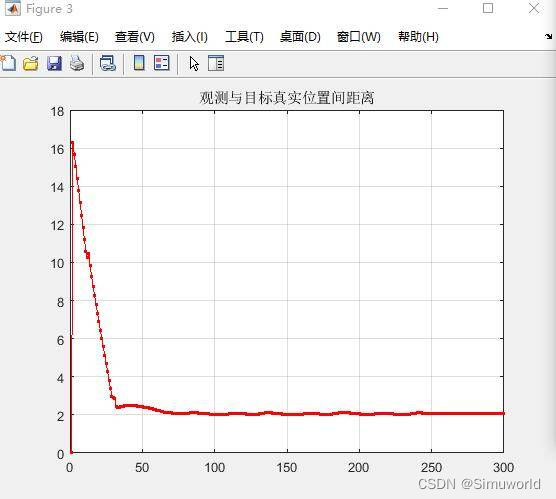
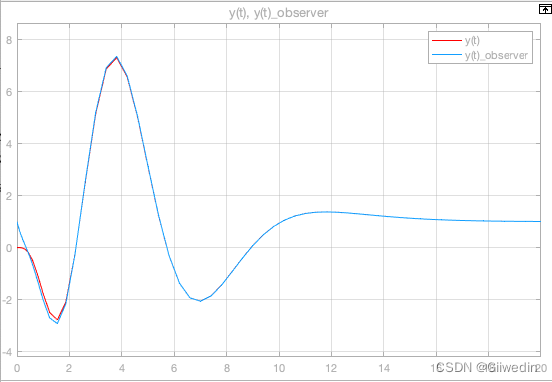
在实时控制系统和信号处理中,观测器和卡尔曼滤波器是两个常用于状态估计的工具。本文将通过 Matlab 演示这两者在一维运动系统中的应用,并深入探讨它们的概念、核心点、异同以及本质。 观测器与卡尔曼滤波器的概念 观测器 观测器是一种用于估计系统状态的机制。通过测量系统的输出和输入,观测器可以估计系统的状态,即使系统的状态无法直接观测。观测器的本质是通过对系统行为的监测,利用系统的动态模型来估
【电机控制】PMSM无感foc控制(七)滑模观测器的应用
0. 前言 前面我们讲解了foc的整个流程框图,如图0-1所示,其中的坐标变换、PID控制以及SVPWM都已讲解完毕,接下来会用通俗易懂的方式(不会涉及到特别复杂难以理解的公式)来讲解滑模观测器是如何得到的反电动势,从而提取出转子位置及转速。 图0-1 FOC双环控制系统框图 1. 滑模观测器 建议大家先看一下滑模观测器的大致概念,不用完全理解,但是
相当于IMU ,GPS,气压计,光流 这些都是作为观测器,起修正作用,可以建立观测方程。
相当于IMU ,GPS,气压计这些都是作为观测器,起修正作用,可以建立观测方程。 视觉里程计好像也是的。视觉里程计的频率也是低于IMU的,所以我有个疑问来了,视觉里程计和IMU的融合是不是和GPS和IMU的融合比较类似?当然是基于滤波的融合,不是基于优化的话。以前的基于EKF的VSLAM是不是这种思路? VSLAM里面观察到特征点也应该是一种观测,就像高翔这里说的, 一种是蒙着眼睛走
线性系统理论 -- 降阶观测器的设计
定理: 若系统能观测,且rankC=m,则系统的状态观测器的最小维数是(n-m)。 线性定常时不变系统方程如下(以三阶(n=3)单入单出系统为例,有m=rankC=1): 取变换阵P,有: 对上述系统方程进行线性变换, 得到如下形式: 输出y直接给出。于是状态估计时,只需对 n-m=2 维的、进行估计即可。这就是说,降阶观测器的维数为n-m=2。 降
【自抗扰控制ADRC】扩张观测器ESO
传送门 前言线性状态观测器龙伯格观测器 非线性状态观测器扩张状态观测器(ESO) 前言 扩张观测器ESO也属于状态观测器中的一种,因此在对ESO展开推导描述前,会以循序渐进的方式引出线性观测器等内容,最后再衍生出对ESO的描述和推导。 线性状态观测器 对于一个线性状态方程而已,它的输出不一定能够完全呈现所有状态变量,这就涉及到关于系统状态方程的可观测性。对于以下的状态方程
ADRC——一阶ESO扩张状态观测器simulink实现及C语言代码
理论部分见我之前的博客,一阶ESO相比起来实现更简单,也更好理解,可帮助新手入门使用。虽然常见的物理系统,绝大多都是二阶系统,如F=ma, 做位置控制时,一般用二阶ESO。但是一阶ESO也有一定的用途,后面有空把之前做的一阶ESO的实际案例开源出来。 simulink模型已上传网盘 链接:https://pan.baidu.com/s/1q7zgYNjGXXrAHaaPCSZq
matlab极点配置已知超调量,利用MATLAB 实现极点配置、设计状态观测器(现代控制).doc...
您所在位置:网站首页 > 海量文档  > 计算机 > matlab 利用MATLAB 实现极点配置、设计状态观测器(现代控制).doc14页 本文档一共被下载:次,您可全文免费在线阅读后下载本文档。 下载提示 1.本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。 2.该文档所得收入(下载+内容+预览三)归上
电机控制学习之路:simulink仿真之龙伯格观测器+锁相环的参数设计
前言 本例中使用的参数设计方法,主要思路为将状态观测器的系统矩阵(A+HC)的特征方程的解视作标准二阶系统传递函数的极点,然后根据不同的带宽设计观测器参数。就笔者的仿真结果来看只要带宽不设计的过于离谱,按本文的方法观测速度都能得到一个可用的结果。带宽越大时,观测器所得电角度的相位滞后越小,高频噪声带来的影响就越大。反之,观测器带宽越小,噪声越小,但是所得电角度相位滞后就越大。如果
STM32F4 磁链观测器+PLL 无感无刷电机位置驱动
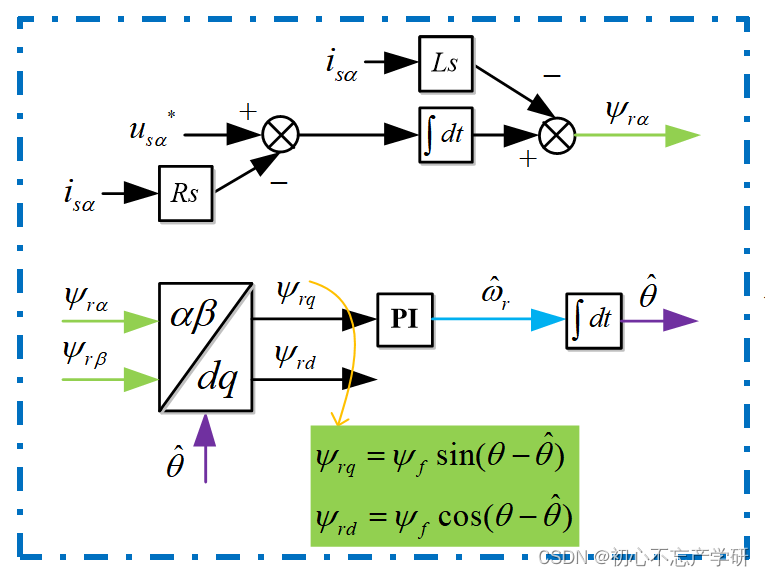
在前面几节我们介绍了基于stm32f1的定点运算的滑膜观测器反正切以及stm32f4的浮点运算滑膜+PLL的案例,大家反馈的还挺好,在做售后的过程中有小伙伴咨询了磁链观测器和隆伯格观测器,针对磁链观测器咨询的较多,我们调试了磁链的程序,以及在这一讲我们将为大家简单讲解一下磁链观测器的使用方法。 硬件测试平台依旧使用我们前面用到的滑膜+PLL的 KY_Motor无刷电机驱动板:
感应异步电机的无传感器矢量控制TMS320F28335,完整的C代码+仿真模型 基于“电压模型+电流模型”的磁链观测器
感应异步电机的无传感器,完整的C代码+仿真模型: 基于“电压模型+电流模型”的磁链观测器,实现转子磁场定向控制(FOC),可实现电机在低速、中高速段的高精度的转速估算; 代码已经成功移植到DSP芯片(TMS320F28335)和STM32F107中,对一台额定功率为33kW的异步电机进行了无传感器矢量控制,波形和试验台架数据见下图。可实现电机带满载零速启动,抗负载扰动性强,响应速度快,控制精度高
基于滑膜观测器锁相环(SMO-PLL)的无传感电机控制simulink仿真
基于滑膜观测器-锁相环的无传感电机控制仿真 仿真图搭建FOC对比SMO接入反馈后的对比总结补充 波形图都直接取自simulink-scope,均未做美化(doge)。 仿真图搭建 观前提示:原理部分请参考袁雷《现代永磁同步电机控制原理及MATLAB仿真》的公式推导。 整体结构: SMO-PLL: SMO: PLL: FOC对比 搭建完模型后先看看FOC
永磁同步电机滑模观测器无位置传感器矢量控制算法仿真模型,基于SMO的PMSM无位置传感器矢量控制算法
永磁同步电机滑模观测器无位置传感器矢量控制算法仿真模型,基于SMO的PMSM无位置传感器矢量控制算法。 其中SMO模块由锁相环组成,不同于反正切函数。 由matlab/simulink搭建,以供参考学习。 ID:72100679743330301阳光彩虹小彪马
基于自适应滑膜观测器的永磁同步电机的无位置传感器控制仿真
1、自适应滑模观测器算法 对于表贴式三相PMSM,重写静止坐标系下的电流方程为 为了设计SMO,首先定义滑模面函数为 设计自适应SMO为 将两个电流方程相减可得 由于系统进人滑模面后,即有 所以可得到 反电动势的自适应律设计为 为了证明自适应SMO的稳定性,定义李雅普诺夫函数为 由于机械时间常数远大于电气时间常数,所以认为转速在一个估算周期内不变,则由自适应律可得 将上式代入
基于滑模观测器的永磁同步电机无位置传感器控制
1、传统滑膜观测器设计 目前,大多数传统SMO算法的设计是基于静止坐标系下的数学模型的,重写电机的电压方程为: 其中:Ld|、Lq为定子电感;we为电角速度;p=d/dt,为微分算子;Uα、Uβ为定子电压,iα,iβ为定子电流,Eα,Eβ为扩展反电动势(EMF),且满足: 对于表贴式三相PMSM(Ld=Lq=L,) ,打展反电动势的表达式(2)将被间化,为仅与电机的转速有关的变量。当转速较快时
使用simulink仿真连续(离散)线性定长系统全维渐进状态观测器
目录 系统模型: 闭环极点设计分离性 设计系统输出反馈系数K 转换标准能控型 设计反馈矩阵G 仿真 matlab代码 simulink模型 仿真结果 仿真程序下载地址:连续定常系统全维状态观测器simulink仿真m代码-智慧城市文档类资源-CSDN下载 全维数字观测器输出反馈-智能家居文档类资源-CSDN下载 系统模型: