本文主要是介绍【自抗扰控制ADRC】扩张观测器ESO,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
传送门
- 前言
- 线性状态观测器
- 龙伯格观测器
- 非线性状态观测器
- 扩张状态观测器(ESO)
前言
扩张观测器ESO也属于状态观测器中的一种,因此在对ESO展开推导描述前,会以循序渐进的方式引出线性观测器等内容,最后再衍生出对ESO的描述和推导。
线性状态观测器
对于一个线性状态方程而已,它的输出不一定能够完全呈现所有状态变量,这就涉及到关于系统状态方程的可观测性。对于以下的状态方程而言
x ′ = A x + B u y = C x x'=Ax+Bu\\ y=Cx x′=Ax+Buy=Cx
其中, x x x为 n n n维列向量,则该状态方程可观测的充要条件为
r a n k ( [ C C A ] ) = n rank(\begin{bmatrix} C\\CA\end{bmatrix})=n rank([CCA])=n
讨论状态观测器的前提是该系统状态方程具有能观测性。
建立状态观测器的原因是,由于实际开发过程中,对于各状态变量的采集存在各类问题,如传感器设备昂贵,无对应状态变量采样条件等。因此可以跟系统状态方程设计虚拟的状态观测器,估计系统的状态向量。
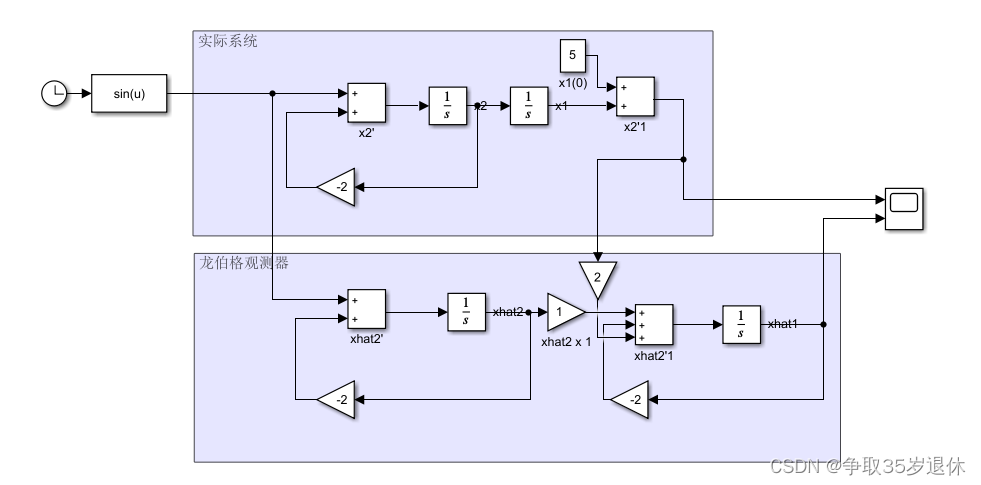
龙伯格观测器
- 理想假设
首先建立
x ′ ^ = A x ^ + B u y ^ = C x ^ \hat{x'} =A\hat{x}+Bu\\ \hat{y}=C\hat{x} x′^=Ax^+Buy^=Cx^
假设系统不存在扰动,且各状态变量初始状态一致,则这个观测器得到的估计值则就完全等同于实际的状态值。但世事难预料,往往实际系统存在扰动,且无法得到各状态的初始状态,则该观测器在实际运行中会因为累计误差而导致状态估计出现严重偏差。因此需要加入修正项进行补偿。 - 修正补偿
令修正项为 L ( y − y ^ ) L(y-\hat{y}) L(y−y^),其中 L L L是修正项增益。将修正项代入后可以得到
x ′ ^ = A x ^ + B u + L ( y − y ^ ) → x ′ ^ = A x ^ + B u + L ( y − C x ^ ) → x ′ ^ = ( A − L C ) x ^ + B u + L y \hat{x'} =A\hat{x}+Bu+L(y-\hat{y})\\ \rightarrow\hat{x'} =A\hat{x}+Bu+L(y-C\hat{x})\\ \rightarrow\hat{x'} =(A-LC)\hat{x}+Bu+Ly\\ x′^=Ax^+Bu+L(y−y^)→x′^=Ax^+Bu+L(y−Cx^)→x′^=(A−LC)x^+Bu+Ly - 增益参数计算
观测器增益 L L L决定了观测器的准确性,定义观测器性能指标 e = x − x ^ e=x-\hat{x} e=x−x^,满足以下关系
e ′ = x ′ − x ′ ^ → e ′ = A x + B u − ( A − L C ) x ^ − B u − L y → e ′ = A x − ( A − L C ) x ^ − L C x → e ′ = ( A − L C ) ( x − x ^ ) → e ′ = ( A − L C ) e e'=x'-\hat{x'}\\ \rightarrow e'=Ax+Bu-(A-LC)\hat{x}-Bu-Ly\\ \rightarrow e'=Ax-(A-LC)\hat{x}-LCx\\ \rightarrow e'=(A-LC)(x-\hat{x})\\ \rightarrow e'=(A-LC)e e′=x′−x′^→e′=Ax+Bu−(A−LC)x^−Bu−Ly→e′=Ax−(A−LC)x^−LCx→e′=(A−LC)(x−x^)→e′=(A−LC)e
关于观测指标 e e e,建立了一个状态方程来进行描述,我们希望这个状态方程的状态向量能够在有限时间能收敛为0。这个指标e的状态方程无输入,即为齐次微分方程组,求解其特征根,并配置观测参数 L L L的值,使特征根的值均处于负平面,即可使观测器在有限时间内完成对实际系统的准确估计(指标误差 e = 0 e=0 e=0)。
以一个简单的例子来加强理解。假设线性系统状态方程为:
[ x 1 ′ x 2 ′ ] = [ 0 1 0 − 2 ] [ x 1 x 2 ] + [ 0 1 ] u y = [ 1 0 ] [ x 1 x 2 ] \begin{bmatrix} x_1' \\x_2' \end{bmatrix}=\begin{bmatrix} 0&1\\0&-2\end{bmatrix} \begin{bmatrix} x_1 \\x_2\end{bmatrix}+\begin{bmatrix} 0 \\1 \end{bmatrix}u\\ y=\begin{bmatrix} 1&0 \end{bmatrix}\begin{bmatrix} x_1 \\x_2 \end{bmatrix} [x1′x2′]=[001−2][x1x2]+[01]uy=[10][x1x2]
该系统的输出只包含了对于 x 1 x_1 x1,为了观测 x 2 x_2 x2,建立龙伯格观测器。设观测器增益 L = [ l 1 l 2 ] L=\begin{bmatrix} l_1 \\l_2 \end{bmatrix} L=[l1l2]。先根据特征点确定增益参数
d e t ( λ I − ( A − L C ) ) = d e t ( [ λ + l 1 − 1 l 2 λ + 2 ] ) = 0 → λ 2 + ( 2 + l 1 ) λ + 2 l 1 + l 2 = 0 det(\lambda I- (A-LC))=det(\begin{bmatrix} \lambda+l_1&-1 \\l_2&\lambda+2 \end{bmatrix})=0\\ \rightarrow \lambda^2+(2+l_1)\lambda+2l_1+l_2=0 det(λI−(A−LC))=det([λ+l1l2−1λ+2])=0→λ2+(2+l1)λ+2l1+l2=0
令极点均位于 λ 1 = λ 2 = − 2 \lambda_1=\lambda_2=-2 λ1=λ2=−2,则可以得到 ( λ + 2 ) 2 = λ 2 + 4 λ + 4 = 0 (\lambda+2)^2=\lambda^2+4\lambda+4=0 (λ+2)2=λ2+4λ+4=0
即
{ 2 + l 1 = 4 2 l 1 + l 2 = 4 → { l 1 = 2 l 2 = 0 \left\{\begin{matrix} 2+l_1=4\\ 2l_1+l2=4 \end{matrix}\right.\\ \rightarrow \left\{\begin{matrix} l_1=2\\ l2=0 \end{matrix}\right.\\ {2+l1=42l1+l2=4→{l1=2l2=0
则可以得到龙伯格观测器,其数学描述为
[ x 1 ′ ^ x 2 ′ ^ ] = [ − 2 1 0 − 2 ] [ x 1 ^ x 2 ^ ] + [ 0 1 ] u + [ 2 0 ] y \begin{bmatrix} \hat{x_1'} \\\hat{x_2'} \end{bmatrix}=\begin{bmatrix} -2&1\\0&-2\end{bmatrix} \begin{bmatrix} \hat{x_1} \\\hat{x_2}\end{bmatrix}+\begin{bmatrix} 0 \\1 \end{bmatrix}u+\begin{bmatrix} 2 \\0 \end{bmatrix}y [x1′^x2′^]=[−201−2][x1^x2^]+[01]u+[20]y
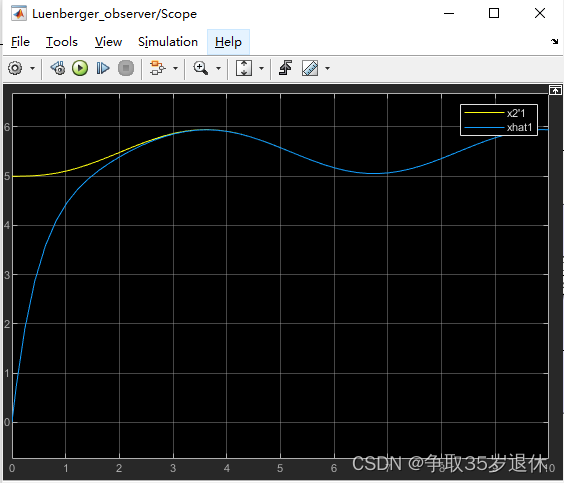
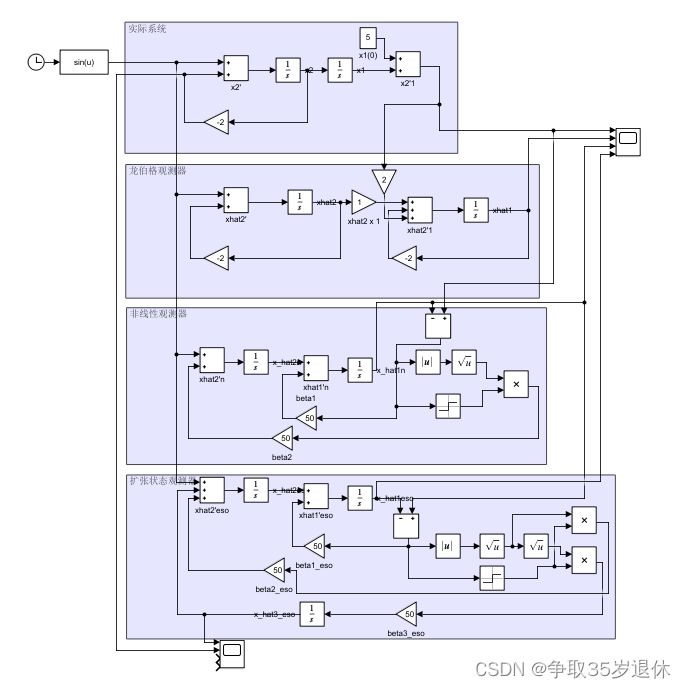
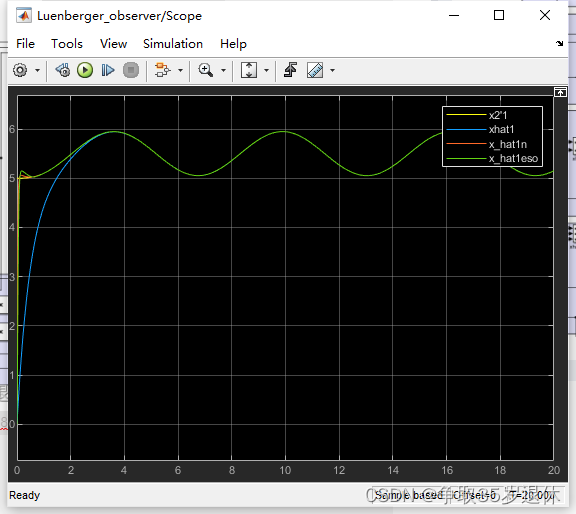
用simulink搭载,仿真观察以下状态观测器估计状态与实际状态的对比。
这里的状态空间的形式是 x1'=x2,x2'=f(x1,x2,u),主要是为了衔接后续的内容,针对的是具有二阶变量的状态变量。即x2是x1的导数,x2对x1具有一定表征能力的特点。
非线性状态观测器
对比龙伯格状态观测器,非线性状态观测器的区别在于对观测器的补偿项是非线性的。
在上面关于补偿项的描述中,采用了线性的误差补偿方法,即 L ( y − y ^ ) = L e L(y-\hat{y})=Le L(y−y^)=Le。除了采用这种方法外,也可以采用一些特殊的非线性函数来进行补偿。
对于满足以下特征的状态空间方程,可以利用这种非线性函数补偿的方式,忽略系统参数及相关关系,进行观测器设计。
{ x 1 ′ = x 2 x 2 ′ = x 3 ⋮ x n − 1 ′ = x n x n ′ = f ( x ⃗ , t , w ) + b u y = x 1 \left\{\begin{matrix} x_1'=x_2 \\ x_2'=x_3\\ \vdots\\ x_{n-1}'=x_n\\ x_n'=f(\vec{x},t,w)+bu\end{matrix}\right.\\ y=x_1 ⎩ ⎨ ⎧x1′=x2x2′=x3⋮xn−1′=xnxn′=f(x,t,w)+buy=x1
令 e = y − y ^ e=y-\hat{y} e=y−y^,则对应的观测器函数为
{ x 1 ′ ^ = x 2 ^ + β 1 g 1 ( e ) x 2 ′ ^ = x 3 ^ + β 2 g 2 ( e ) ⋮ x n − 1 ^ ′ = x n ^ + β n − 1 g n − 1 ( e ) x n ^ ′ = b u + β n g n ( e ) \left\{\begin{matrix} \hat{x_1'}=\hat{x_2} + \beta_1g_1(e)\\ \hat{x_2'}=\hat{x_3} + \beta_2g_2(e)\\ \vdots\\ \hat{x_{n-1}}'=\hat{x_n} + \beta_{n-1}g_{n-1}(e)\\ \hat{x_n}'=bu + \beta_{n}g_{n}(e) \end{matrix}\right. ⎩ ⎨ ⎧x1′^=x2^+β1g1(e)x2′^=x3^+β2g2(e)⋮xn−1^′=xn^+βn−1gn−1(e)xn^′=bu+βngn(e)
其中, β n \beta_n βn是观测器增益,类似于上面龙伯格观测器中 l n l_n ln, g n ( e ) g_n(e) gn(e)是非线性函数,其表达式为
g n ( e ) = ∣ e ∣ 1 2 n − 1 s i g n ( e ) g_n(e)=\left | e\right | ^{\frac{1}{2^{n-1}}}sign(e) gn(e)=∣e∣2n−11sign(e)
这个非线性函数本质上就是对于不同阶数状态空间观测的误差响应,这种误差响应排除掉了系统参数,外部扰动,时变性的影响,属于一种具有泛化特性的误差响应机制。
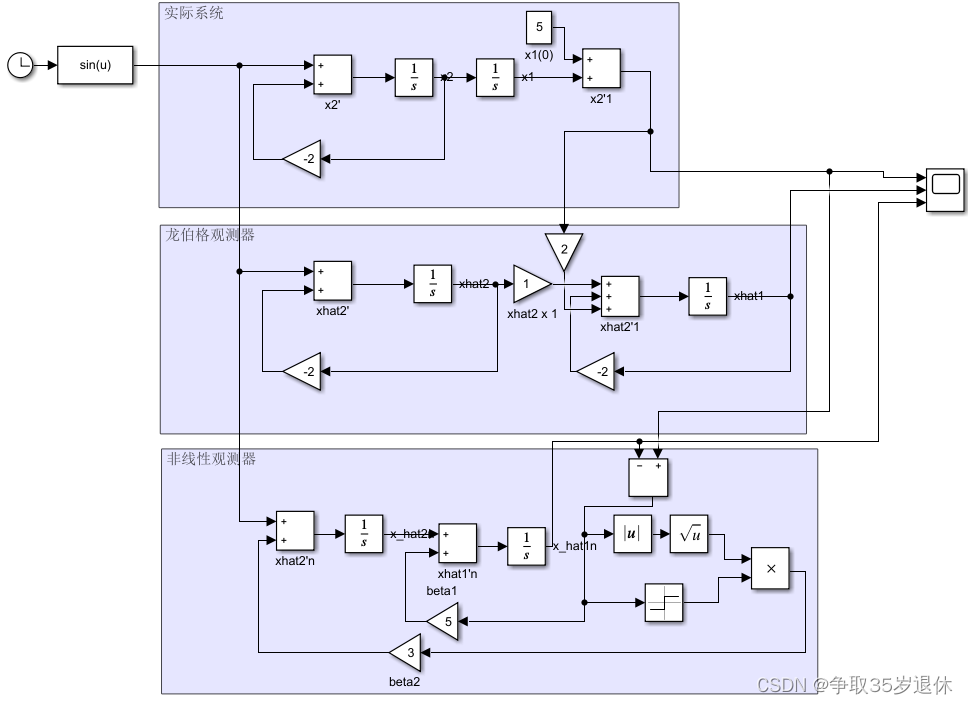
为了对比观测器的性能,同样用上面用到的模型,建立非线性观测器。
[ x 1 ′ x 2 ′ ] = [ 0 1 0 − 2 ] [ x 1 x 2 ] + [ 0 1 ] u y = [ 1 0 ] [ x 1 x 2 ] \begin{bmatrix} x_1' \\x_2' \end{bmatrix}=\begin{bmatrix} 0&1\\0&-2\end{bmatrix} \begin{bmatrix} x_1 \\x_2\end{bmatrix}+\begin{bmatrix} 0 \\1 \end{bmatrix}u\\ y=\begin{bmatrix} 1&0 \end{bmatrix}\begin{bmatrix} x_1 \\x_2 \end{bmatrix} [x1′x2′]=[001−2][x1x2]+[01]uy=[10][x1x2]
建立非线性观测器,其数学描述为
{ x 1 ^ ′ = x 2 ^ + β 1 g 1 ( e ) = x 2 ^ + β 1 e x 2 ^ ′ = u + β 2 g 2 ( e ) = u + β 2 ∣ e ∣ s i g n ( e ) \left\{\begin{matrix} \hat{x_1}'=\hat{x_2}+\beta_1g_1(e) =\hat{x_2}+\beta_1e\\ \hat{x_2}'=u+\beta_2g_2(e)=u+\beta_2 \sqrt{\left | e\right | } sign(e) \\\end{matrix}\right.\\ {x1^′=x2^+β1g1(e)=x2^+β1ex2^′=u+β2g2(e)=u+β2∣e∣sign(e)
上simulink,搭建非线性观测器模型
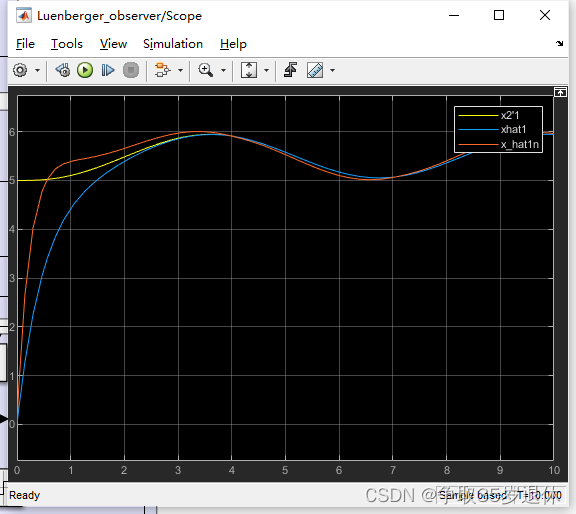
这里观测增益参数分别为5和3,这两个参数影响观测器收敛速度,具体要怎么调,可以对比不同参数下的观测效果
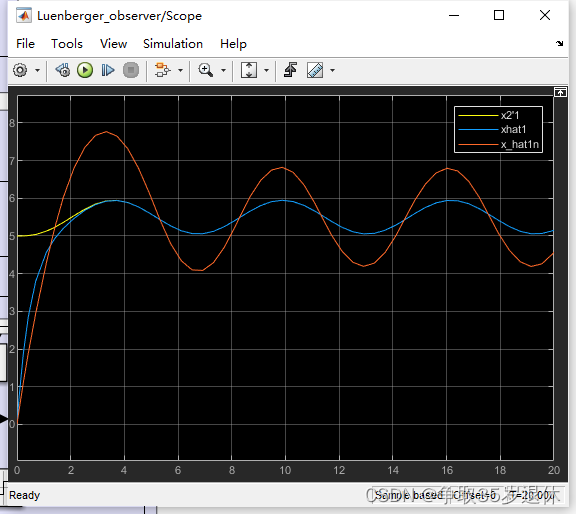
当 β 1 = 1 , β 2 = 1 \beta_1=1,\beta_2=1 β1=1,β2=1时
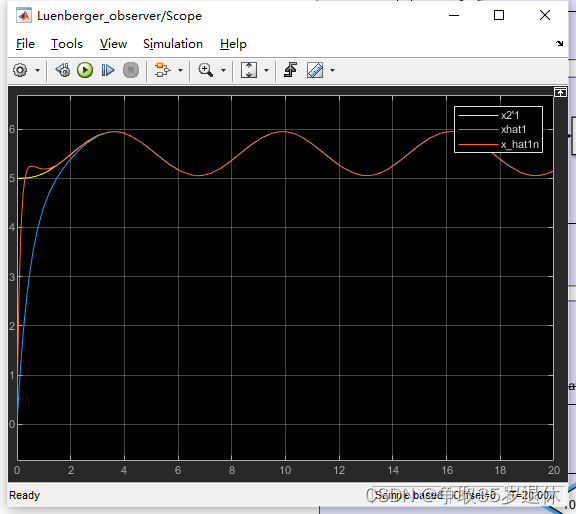
当 β 1 = 10 , β 2 = 10 \beta_1=10,\beta_2=10 β1=10,β2=10时
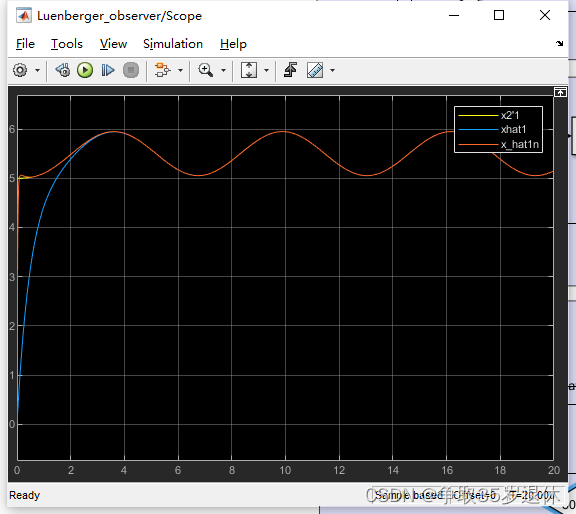
当 β 1 = 50 , β 2 = 50 \beta_1=50,\beta_2=50 β1=50,β2=50时
看起来似乎越大越好,但我认为在实际开发中,由于观测器往往是离散的而非理想的连续系统,因此增益过大会导致振荡的问题。
扩张状态观测器(ESO)
我个人学习东西喜欢进行比较,对比非线性观测器,ESO扩张了什么,又有什么作用,这是我学习这部分内容一直思考的问题。后续的叙述也主要是围绕这几个问题展开。
- 扩张了什么 —— 扩张了对扰动的观测
在非线性观测器中,由于引入了非线性误差补偿修正项,可以忽略系统的各项参数、相互关系及扰动,数学描述为 f ( x ⃗ , w , t ) f(\vec{x},w,t) f(x,w,t),在实际的很多系统中,对于系统参数、相互关系及随机扰动都是未知的,无法精确描述的内容,因此非线性观测器的优势就体现出来了,可以忽略这部分内容进行观测。
注:个人认为在系统中,未知的东西就是扰动。
如果,我是说如果,我们将这部分扰动也观测出来,并且将观测结果通过输入抵消掉,那就可以极大的提高控制器的性能。
为了实现这个目的,我们就需要扩张一个状态变量,用于描述这个扰动。即在 n n n维状态空间中,扩展 n + 1 n+1 n+1的状态变量 x n + 1 = f ( x ⃗ , w , t ) x_{n+1}=f(\vec{x},w,t) xn+1=f(x,w,t),则状态空间扩张为:
{ x 1 ′ = x 2 x 2 ′ = x 3 ⋮ x n − 1 ′ = x n x n ′ = x n + 1 + b u x n + 1 ′ = f ′ ( x ⃗ , w , t ) \left\{\begin{matrix} x_1'=x_2 \\ x_2'=x_3\\ \vdots\\ x_{n-1}'=x_n\\ x_n'=x_{n+1}+bu\\ x_{n+1}'=f'(\vec{x},w,t)\end{matrix}\right.\\ ⎩ ⎨ ⎧x1′=x2x2′=x3⋮xn−1′=xnxn′=xn+1+buxn+1′=f′(x,w,t)
将状态空间扩张后,重新走一遍非线性状态观测器的路子。
令 e = y − y ^ e=y-\hat{y} e=y−y^,则对应的观测器函数为
{ x 1 ′ ^ = x 2 ^ + β 1 g 1 ( e ) x 2 ′ ^ = x 3 ^ + β 2 g 2 ( e ) ⋮ x n − 1 ^ ′ = x n ^ + β n − 1 g n − 1 ( e ) x n ^ ′ = x n + 1 ^ + b u + β n g n ( e ) x n + 1 ^ ′ = β n + 1 g n + 1 ( e ) \left\{\begin{matrix} \hat{x_1'}=\hat{x_2} + \beta_1g_1(e)\\ \hat{x_2'}=\hat{x_3} + \beta_2g_2(e)\\ \vdots\\ \hat{x_{n-1}}'=\hat{x_n} + \beta_{n-1}g_{n-1}(e)\\ \hat{x_n}'=\hat{x_{n+1}}+bu + \beta_{n}g_{n}(e) \\ \hat{x_{n+1}}'=\beta_{n+1}g_{n+1}(e) \\ \end{matrix}\right. ⎩ ⎨ ⎧x1′^=x2^+β1g1(e)x2′^=x3^+β2g2(e)⋮xn−1^′=xn^+βn−1gn−1(e)xn^′=xn+1^+bu+βngn(e)xn+1^′=βn+1gn+1(e) - 有什么作用
扩张的这部分对于扰动的观测,主要是用于ADRC控制器的扰动补偿环节,除此之外,我们可以继续用上面的案例来观察在一样参数的情况,ESO的观测性能会不会得到提高。
{ x 1 ^ ′ = x 2 ^ + β 1 g 1 ( e ) = x 2 ^ + β 1 e x 2 ^ ′ = x 3 ^ + u + β 2 g 2 ( e ) = x 3 ^ + u + β 2 ∣ e ∣ s i g n ( e ) x 3 ^ ′ = β 3 g 3 ( e ) = β 3 ∣ e ∣ 1 4 s i g n ( e ) \left\{\begin{matrix} \hat{x_1}'=\hat{x_2}+\beta_1g_1(e) =\hat{x_2}+\beta_1e\\ \hat{x_2}'=\hat{x_3}+u+\beta_2g_2(e)=\hat{x_3}+u+\beta_2 \sqrt{\left | e\right | } sign(e)\\ \hat{x_3}'=\beta_3g_3(e)=\beta_3\left | e\right |^{\frac{1}{4}} sign(e) \\\end{matrix}\right.\\ ⎩ ⎨ ⎧x1^′=x2^+β1g1(e)=x2^+β1ex2^′=x3^+u+β2g2(e)=x3^+u+β2∣e∣sign(e)x3^′=β3g3(e)=β3∣e∣41sign(e)
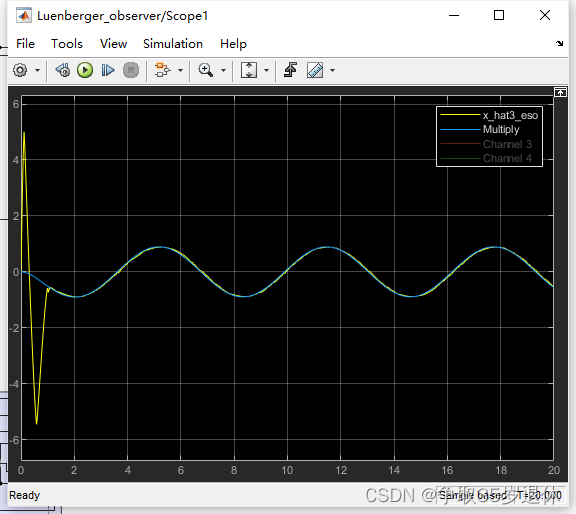
上simulink,设计EOC观测器
根据定义的系统,这部分扰动的表达式为 f ( x ⃗ , w , t ) = − 2 x 2 f(\vec{x},w,t)=-2x_2 f(x,w,t)=−2x2,一开始的偏差是由于 x 1 ( 0 ) ≠ 0 x_1(0)\ne0 x1(0)=0,但也能够很快收敛。
这篇关于【自抗扰控制ADRC】扩张观测器ESO的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!