本文主要是介绍电机控制学习之路:simulink仿真之龙伯格观测器+锁相环的参数设计,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
本例中使用的参数设计方法,主要思路为将状态观测器的系统矩阵(A+HC)的特征方程的解视作标准二阶系统传递函数的极点,然后根据不同的带宽设计观测器参数。就笔者的仿真结果来看只要带宽不设计的过于离谱,按本文的方法观测速度都能得到一个可用的结果。带宽越大时,观测器所得电角度的相位滞后越小,高频噪声带来的影响就越大。反之,观测器带宽越小,噪声越小,但是所得电角度相位滞后就越大。如果对观测器性能要求较高,还需要手动调整PI参数,或者换个更好的观测器模型。
网上还有另一种常见的观测器参数设计方法,可以参考意法半导体的《STM32电动机控制应用系列讲座之三——ST MC SDK 5.x 相电流检测与重构 位置、速度信息获取》,链接:STM32电动机控制应用系列讲座之三:ST MC SDK 5.x 相电流检测与重构位置、速度信息获取 | STMCU中文官网
从笔者的仿真结果来看,两种方法取得的效果基本相同。
最后,如若本文有谬误之处,请于评论区指出,笔者会不断更正补充。
龙伯格观测器参数设计
一、龙伯格观测器观测原理
龙伯格观测器即为状态观测器,它的原理可以参考《现代控制理论(第3版》(刘豹,唐万生) ,或者参考:STM32G0无刷电机控制--龙伯格观测器建立_哔哩哔哩_bilibili
可以将一个线性系统表示为状态空间方程:
对于 PMSM电机,其定子电流和反电动势模型如下:
其中:
我们可以将以上模型表示成状态空间方程的形式,首先,将两相旋转电流的微分和两相旋转反电动势的微分作为状态量,于是有:
![]()
然后将两相旋转电压(已知的设定量)作为输入量矩阵, 两相静止电流(可用传感器测量的量)作为输出量矩阵:
![]()
![]()
此后,通过对比观察我们建立的模型方程组可以得出状态转移矩阵A为:
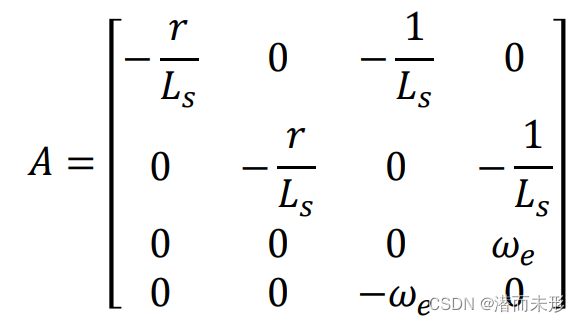
输入控制矩阵B为:
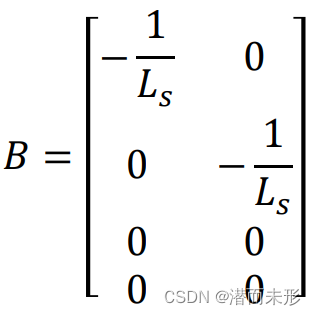
最后,因为我们可以直接测出三相电流后直接转换成两相静止电流,且输出量中没有反电动势,所以C矩阵为:
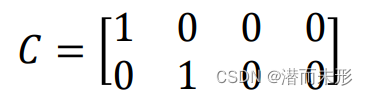
综上,我们根据物理模型和实际的测量量构建出了一个实际的系统,该系统的输入输出量皆为真实量。但是,该系统中包含了速度信息的反电动势部分是无法测量的。此外,从输入控制矩阵和输出矩阵中都没有三、四两行可知:我们无法直接通过输入输出构建出反电动势的值。
因此,我们需要观测器来观测出无法直接得到的状态量。
构造龙伯格观测器,首先需要构建出一个各个系数矩阵与实际系统相同的观测系统,形式仍为:
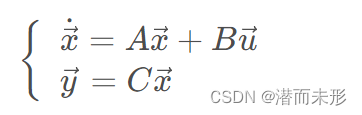
然而,观测系统只有输入量是真实的已知的,状态量和实际系统测量得出的输出量均为“估计值”。
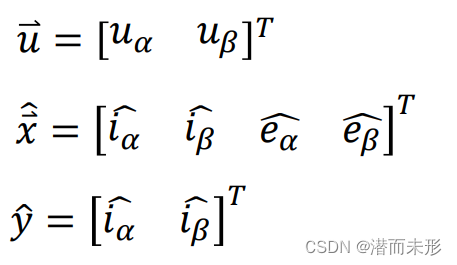
显然,光有观测系统毫无意义,观测系统中不但同样无法得到反电动势的数值,甚至连实际系统中可以测量的电流量,在观测系统中也是一个不准确的任意值。
于是,我们需要需要对观测系统中的各个状态量进行“修正”,修正的方法就是“反馈”:
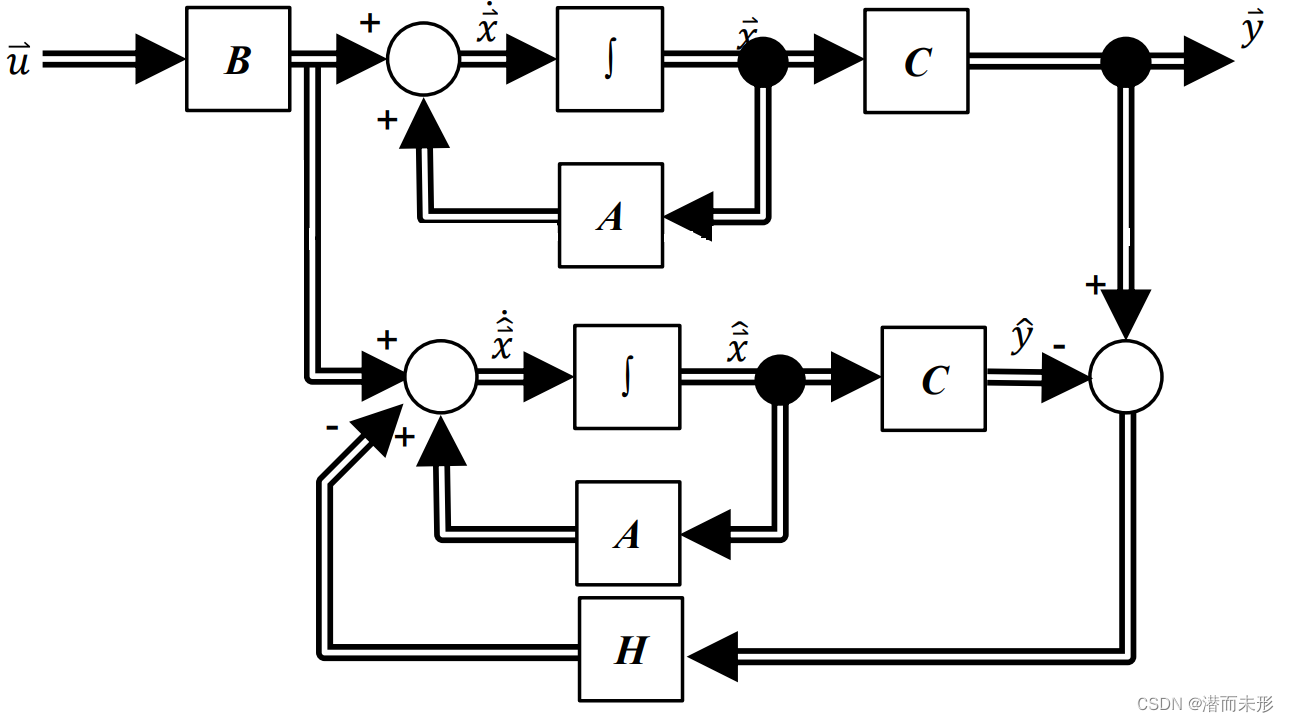
如图所示,上半部分为实际系统,有着真实的测量得出的输出量。真实输出量与下半部分中的观测系统的观测输出量的差值,乘一个反馈增益矩阵之后,和输入量一起修正状态量的观测值。
于是有:

重新观察A矩阵:
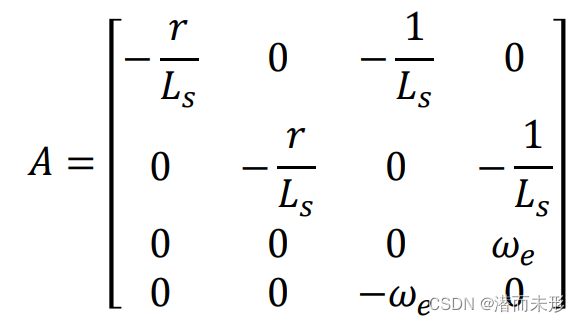
显然,前两行系数错位但相同。后两行虽然系数不同,但是we是一个变化值,为了便于计算,都会作去耦(we=0)处理。去耦后,A矩阵后两行完全相等。于是,我们可以把原来四阶的A矩阵可以视作两个错位但系数相同的两阶的矩阵拼合而成(一、三两行;二、四两行),这就是龙伯格观测器的降阶处理。
降阶后,反馈增益矩阵也变得只需要两个系数:h1、h2。
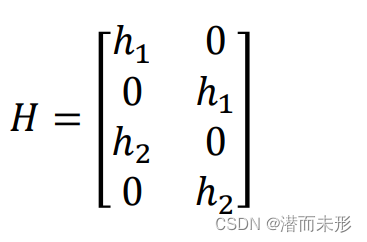
此时,结合![]() 易得(A+HC)为反馈调节后观测系统的新状态转移矩阵,且有:
易得(A+HC)为反馈调节后观测系统的新状态转移矩阵,且有:
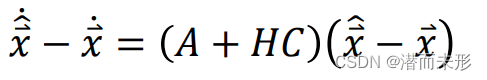
于是,观测系统的状态量估计值与实际系统的状态量实际值的差值为:

易知,只要(A+HC)这个状态转移矩阵的特征值均有负实部,该差值必然在经过足够长的时间后收敛到零,于是观测系统便得到了真实系统中各个状态量的实际值。
以上就是龙伯格观测器的原理,一句话概括:通过观测输出和实际输出的差值来修正观测系统的所有状态量,当观测系统中电流项修正到真实值(测量值)时,不可测量的反电势也会被修正到真实值。
二、龙伯格观测器反馈增益系数计算
法一:
对于一个状态空间方程,其状态转移矩阵又被称为系统矩阵。系统矩阵的零、极点,即为系统传递函数的零、极点。
在前文中,我们已经知道了加入输出反馈后,观测系统新的系统矩阵为:A+HC
因此,令|λI-(A+HC)|=0,即可得出系统矩阵的特征方程:
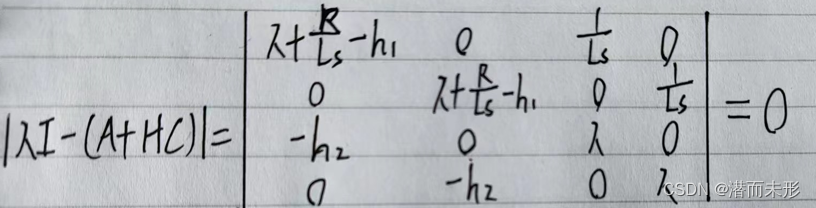
简单计算后可解出λ的值:

为了使观测值和实际值差值最终能收敛到0,系统矩阵所有极点都应该具有负实部,于是h1、h2的值应该满足:h1<r/Ls,h2>0.
对上式变形可知:

于是,我们得到了反馈增益系数h1、h2与系统传递函数极点λ1、λ2的关系。
然后,可以把系统视为一个有两个极点的二阶系统,参考胡寿松的《自动控制原理》:
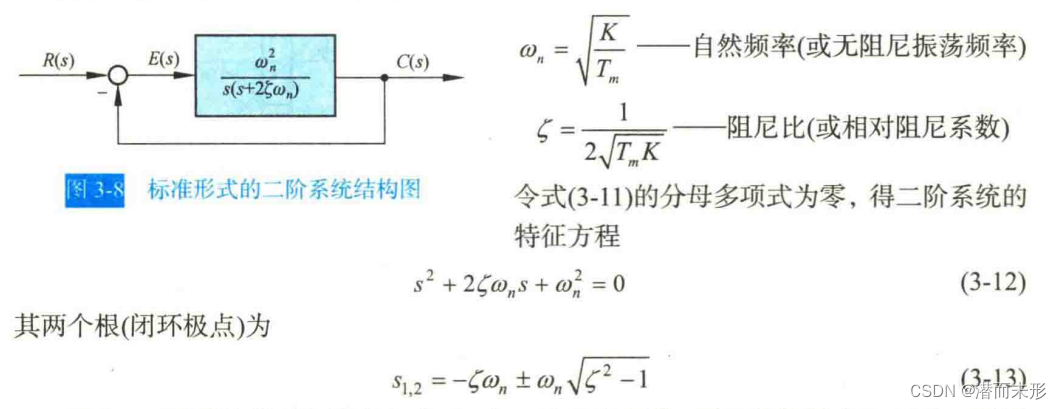
于是,h1、h2的值为:
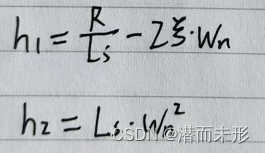
其中,阻尼比ξ可直接设为1,然后调节Wn的值即可:
Wn的值取决于系统带宽和ξ,二者的关系为:
 带宽越大,对高频信号的响应越大,能使得系统响应速度提高,但是高频噪声的影响也会变大。
带宽越大,对高频信号的响应越大,能使得系统响应速度提高,但是高频噪声的影响也会变大。
当带宽较小时,例如,将Wn设为600Hz时:
速度观测效果: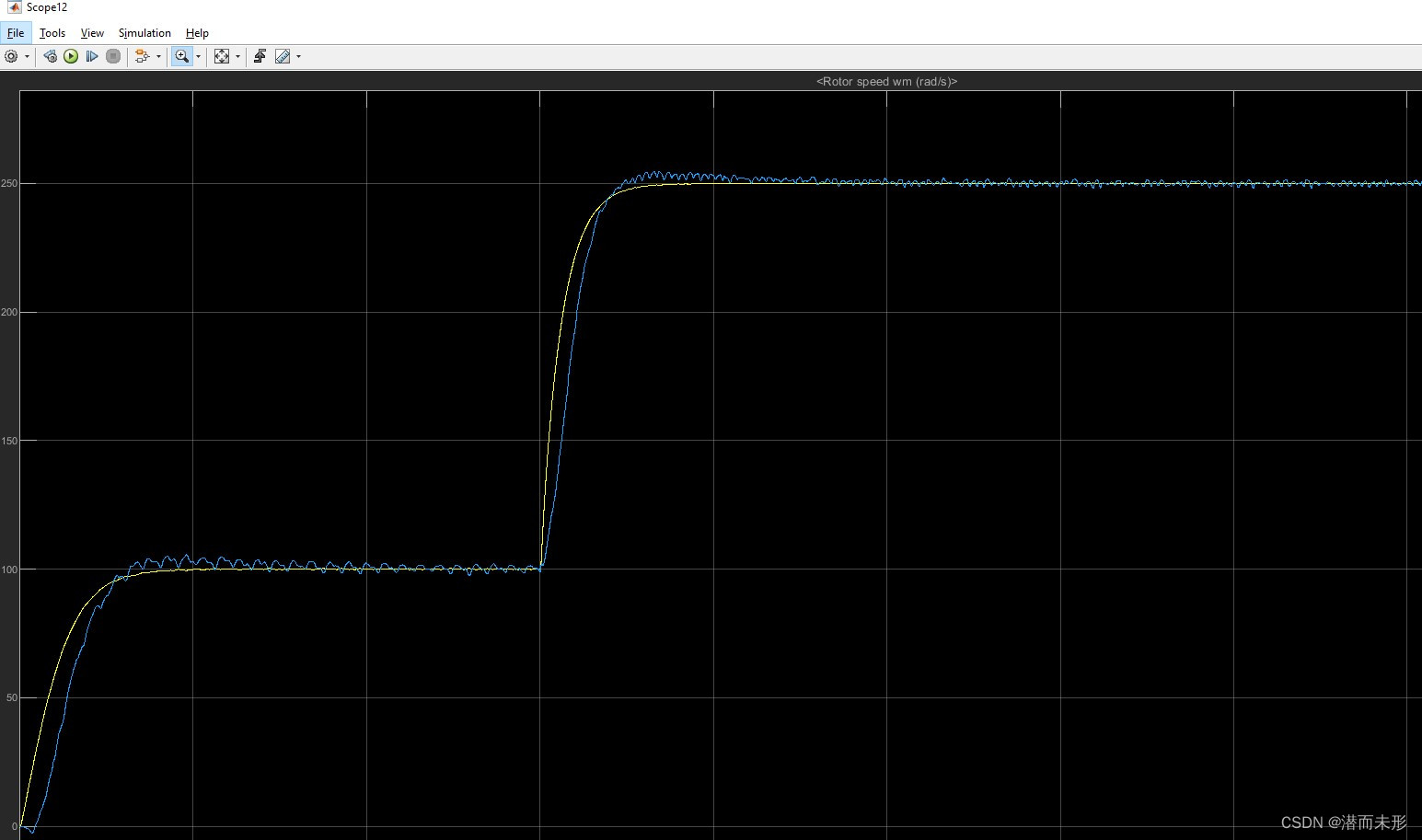
滤波后: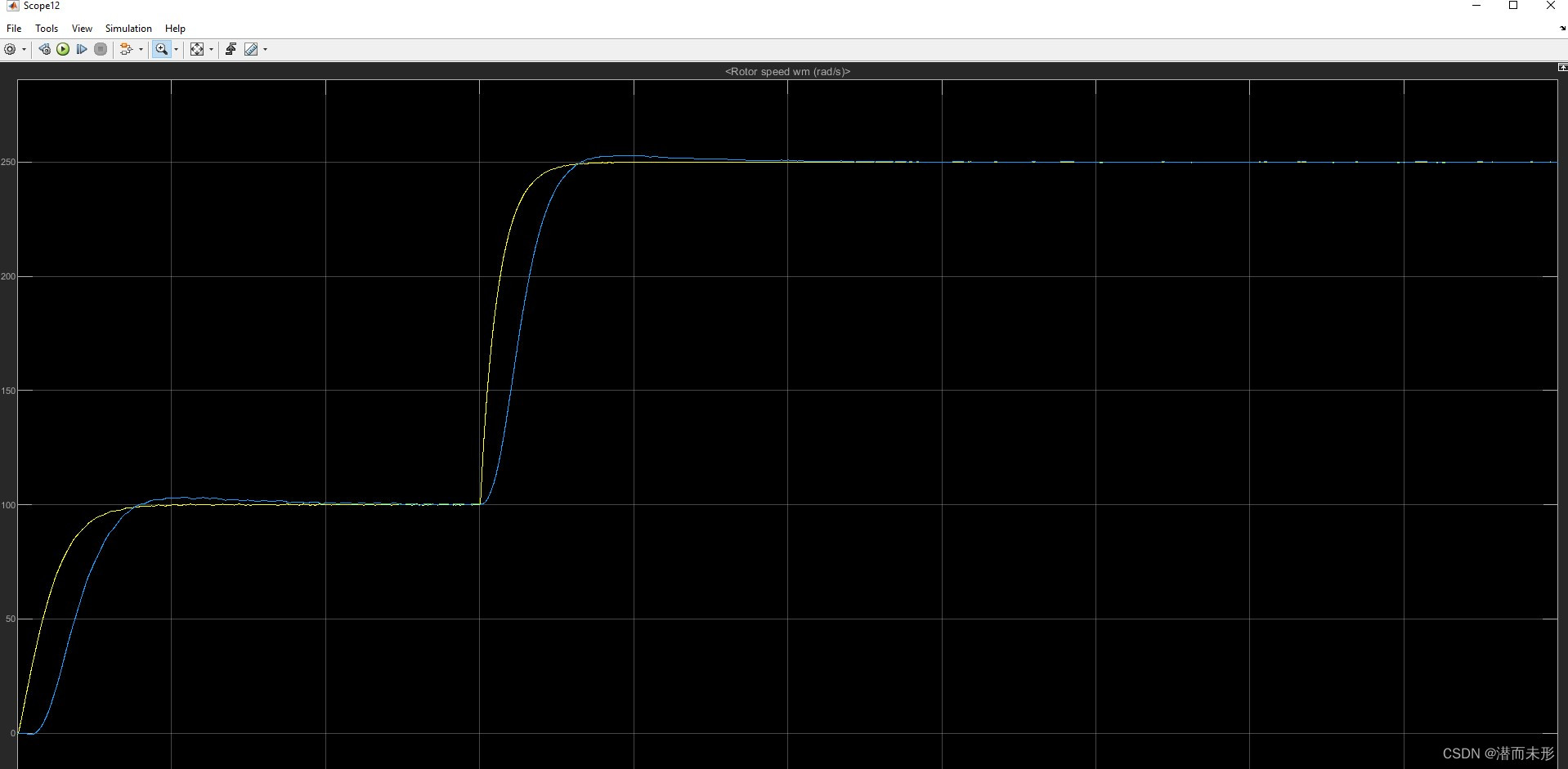
角度观测效果:
当带宽较大时,例如,将Wn设为6000Hz时:
速度观测效果: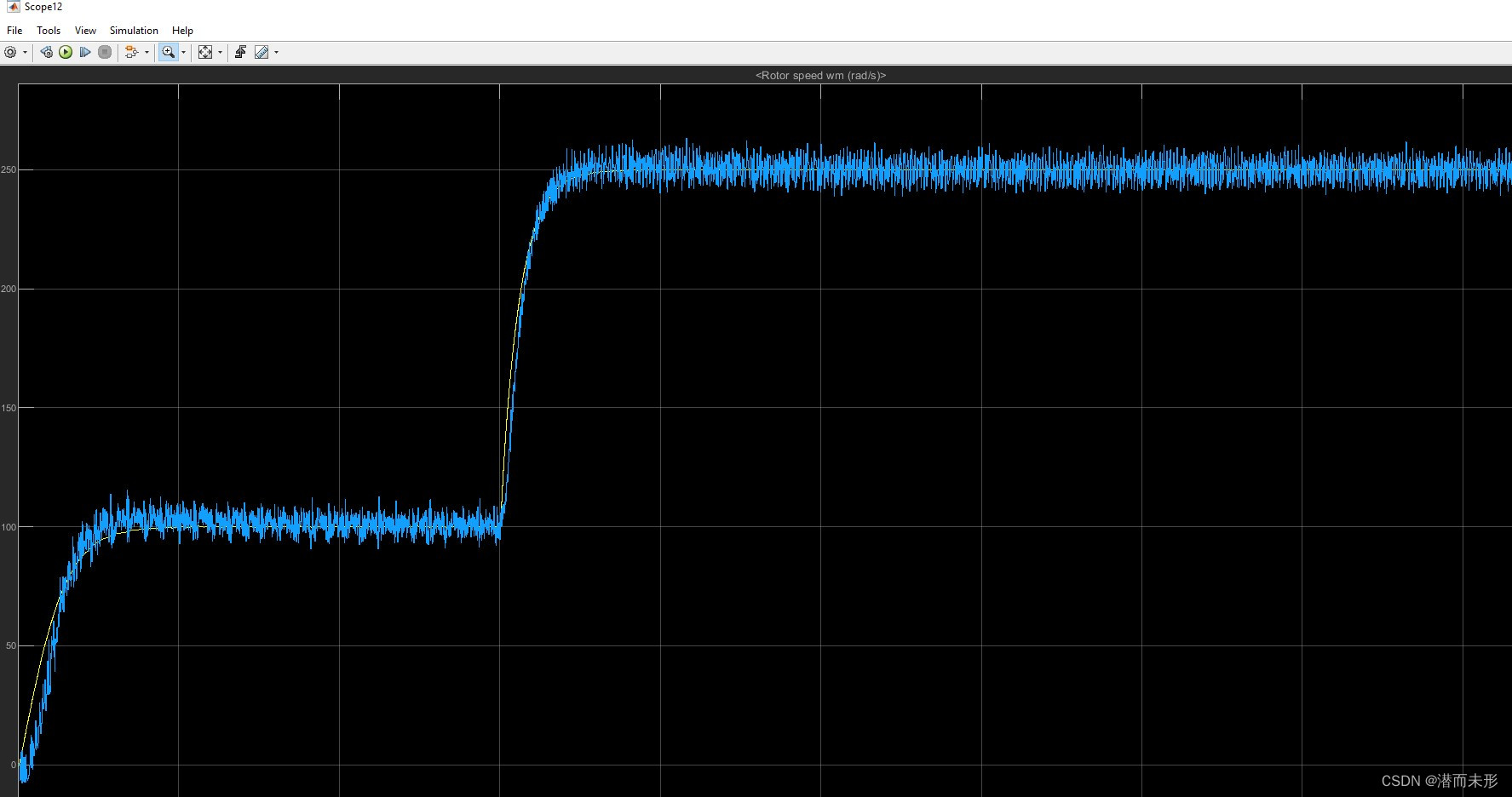
滤波后: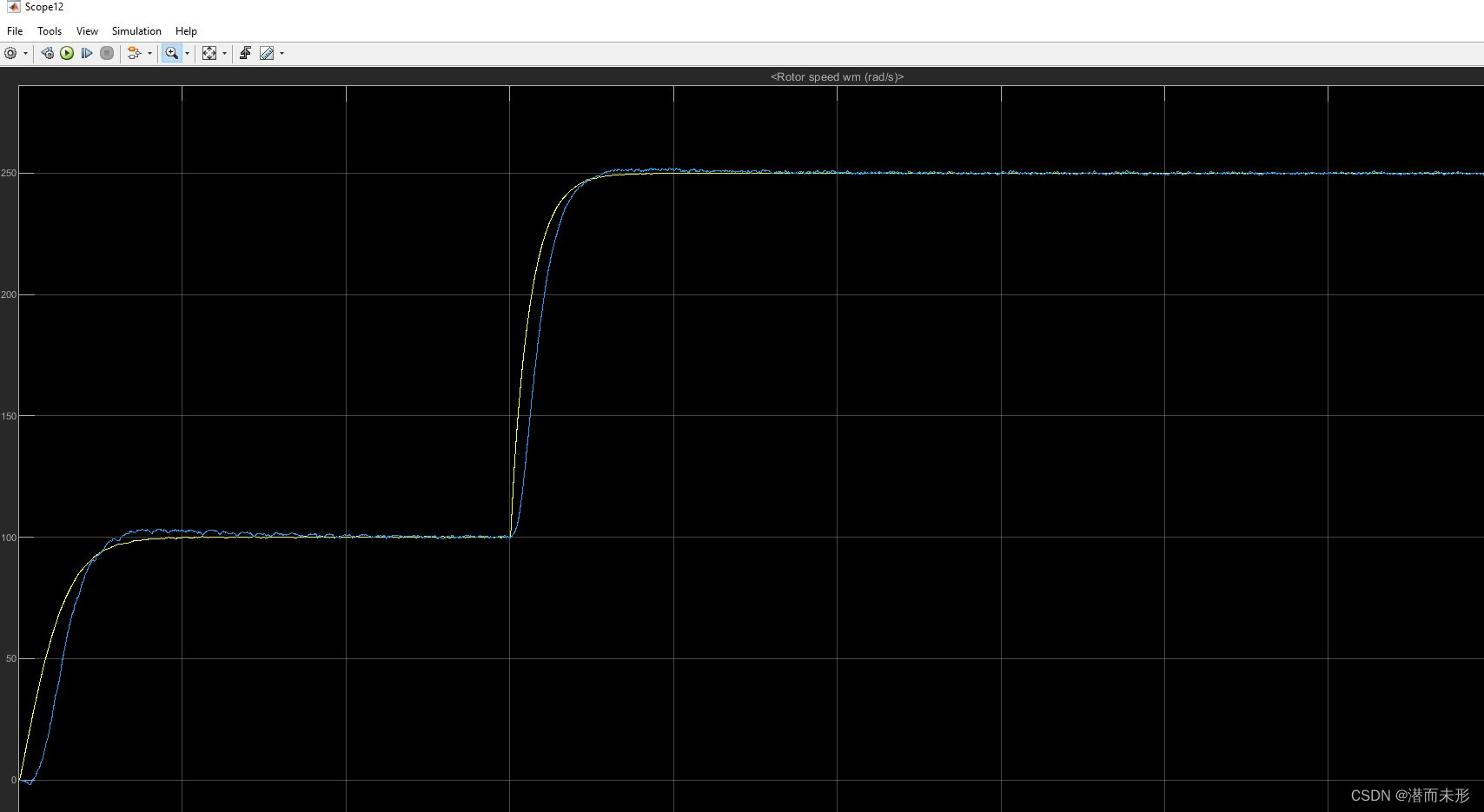
角度观测效果:
由上可知,带宽越大,角度观测效果越好。速度观测效果滤波后都差不多,影响不大,但是观测器带宽接近速度环带宽时,即使不滤波,响应曲线也足够平滑。
法二:
可以直接参考意法半导体的《STM32电动机控制应用系列讲座之三——ST MC SDK 5.x 相电流检测与重构 位置、速度信息获取》,链接:STM32电动机控制应用系列讲座之三:ST MC SDK 5.x 相电流检测与重构位置、速度信息获取 | STMCU中文官网
或者参考B站视频:STM32G0无刷电机控制--龙伯格观测器建立_哔哩哔哩_bilibili
该方法会对状态空间方程通过向前欧拉的方式进行离散化,然后只需要选定不同的k值,然后即可根据公式计算h1、h2参数:
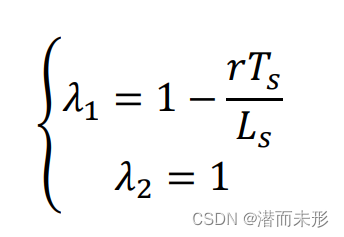
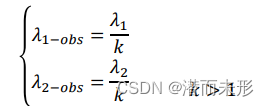
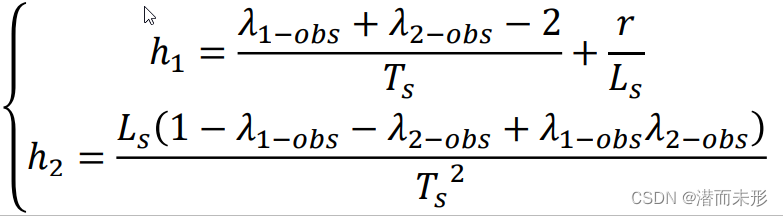
当k取1.5时:
速度观测效果:
滤波后: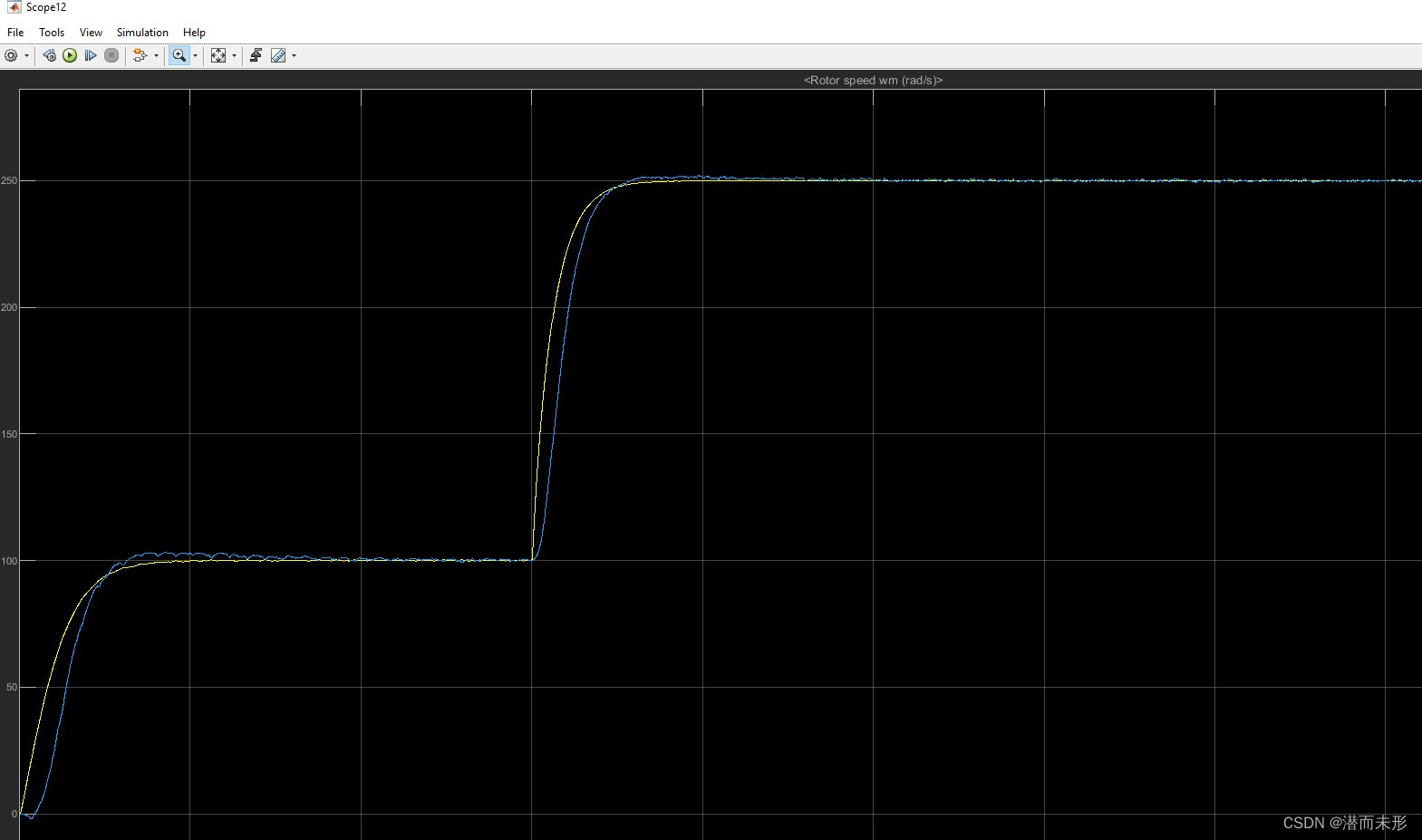
角度观测效果:
当k取4时:
速度观测效果: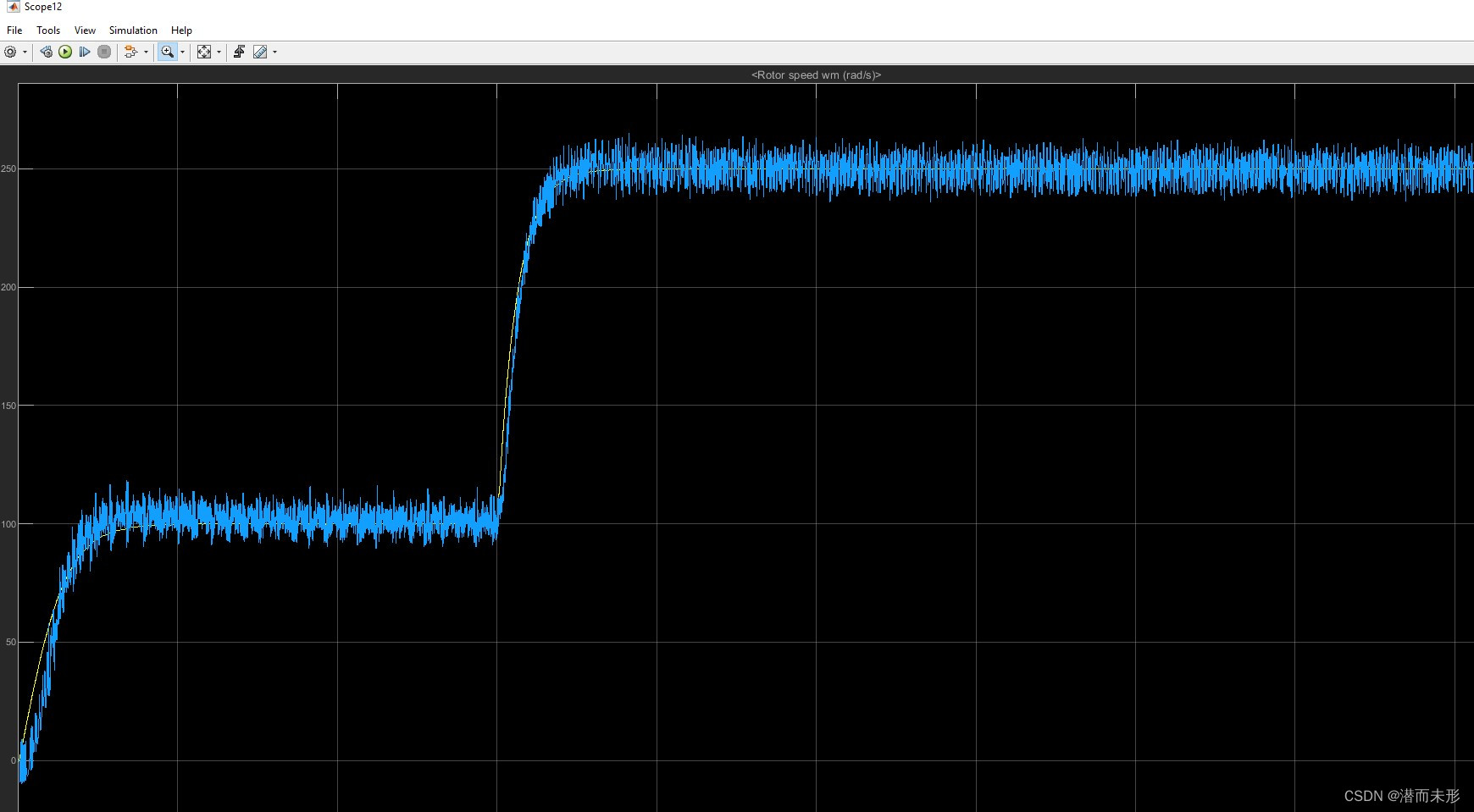
滤波后: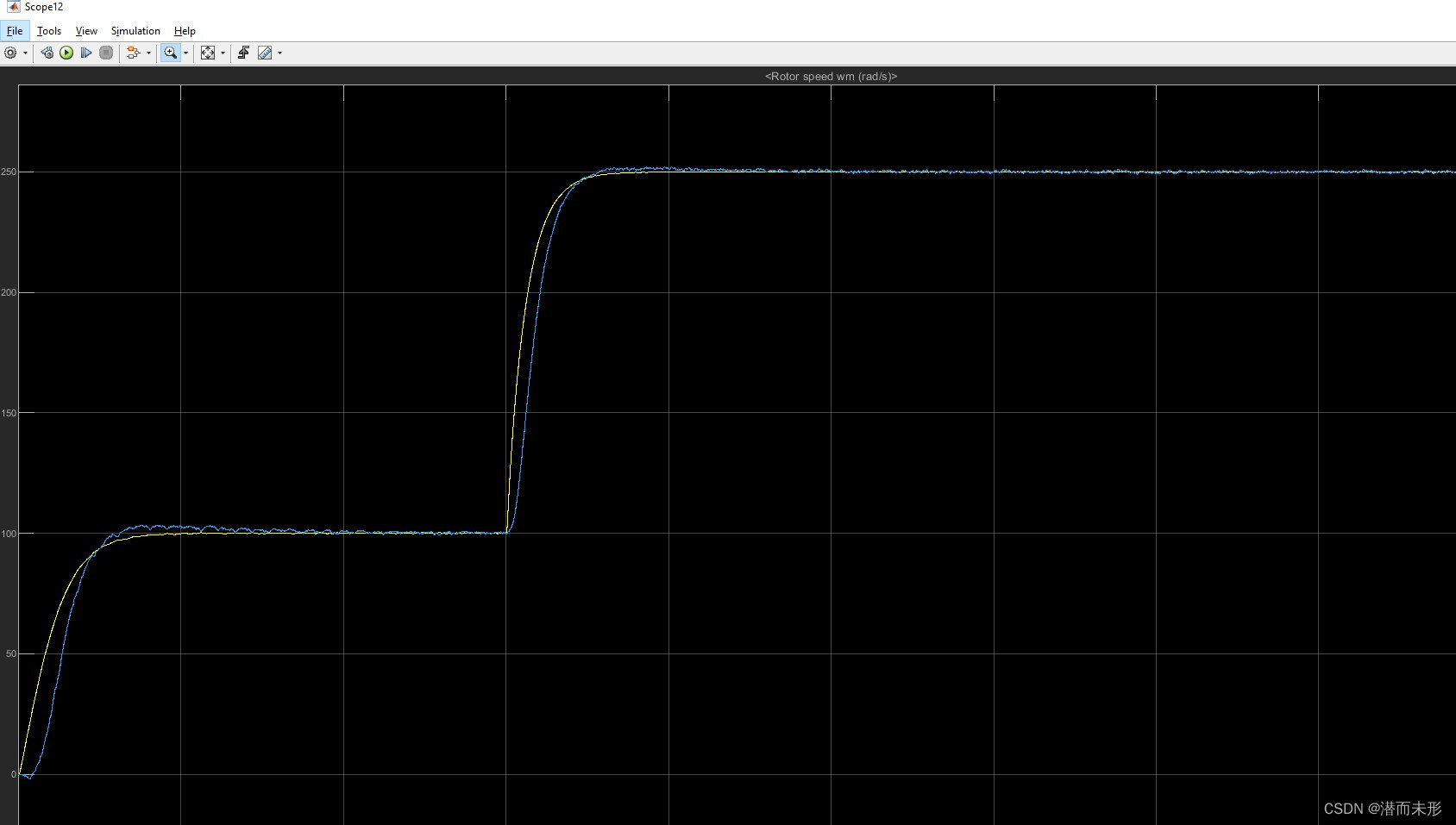
角度观测效果: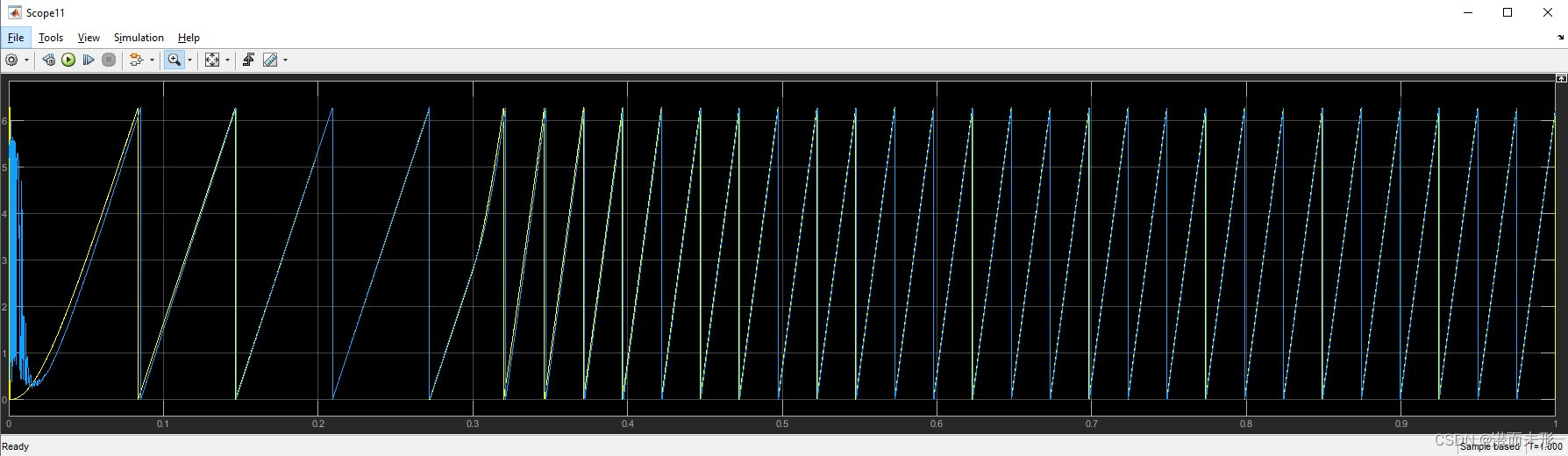
小结
由上可知:两种方法就效果来说差不多,法二的k越大,相当于法一的带宽越大。相对来说,法一在设计h1、h2时可以设定的参数多了一个阻尼比ξ,且带宽的选择更直观。所以设计过程中法一更灵活,法二更方便。 此外,法二在设计时考虑到了离散步长,法一在设计时未进行离散化。所以法二可能拥有更好的效果?但是就笔者的仿真结果来看,未发现法二的观测效果有明显优势。
锁相环参数设计
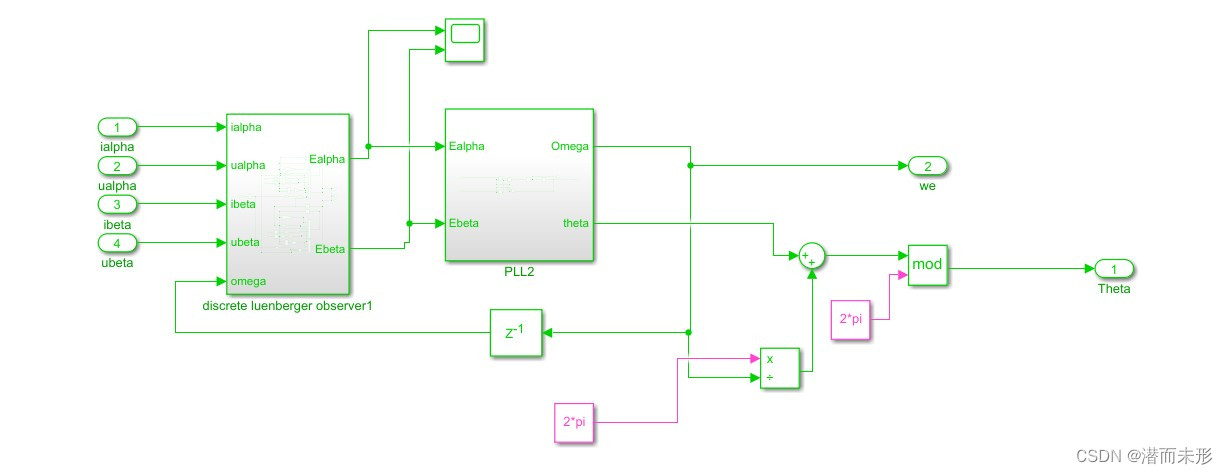
锁相环的作用是提取龙伯格观测器观测出的反电动势信号中包含的角速度信息,并对其积分后得出电角度。
模型获取可以去B站UP欧拉电子的个人空间_哔哩哔哩_bilibili的相关视频中扫码关注他的淘宝店铺后找客服获取,为避免影响UP主引流效果,本处只贴一个锁相环和龙伯格观测器连接结构。
网上有很多讲述锁相环结构和原理的文章,笔者建议参考这两篇:SPMSM控制——无感锁相环参数是怎么来的 - 知乎 (zhihu.com)
手撕系列(3):锁相环(SRF-PLL) - 知乎 (zhihu.com)
锁相环结构如下:
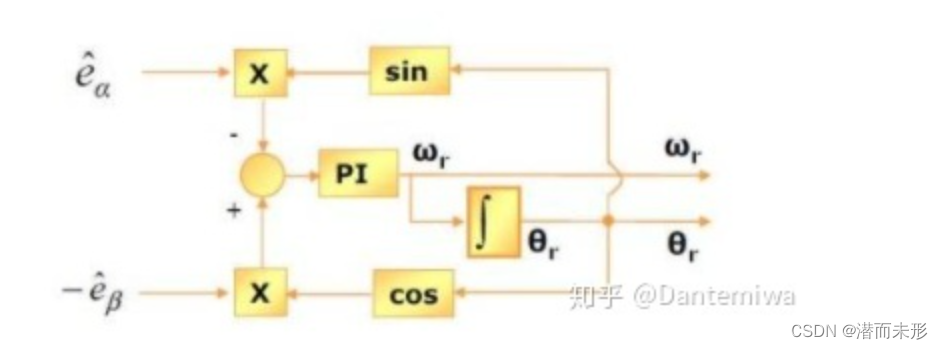
锁相环传递函数如下:
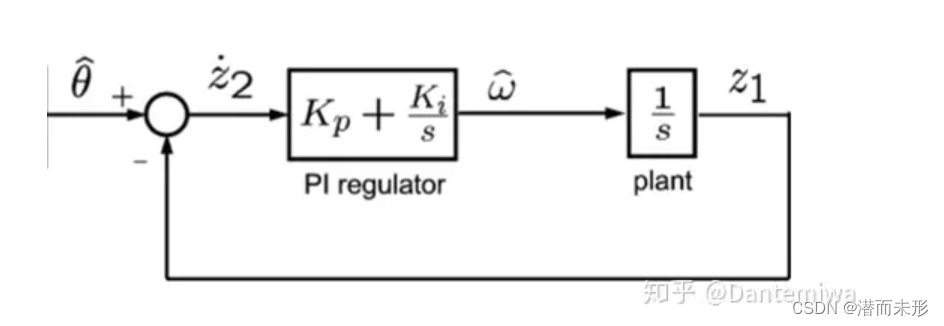
显然:该锁相环为二阶系统
PI参数计算公式如下:
其中,wc的位置上其实应该是自然频率wn,但是在这里被近似当做带宽wc来计算。带宽代表着系统的响应速度,带宽越大,响应越快,高频噪声影响越大。
ξ是二阶系统阻尼比,主要影响超调量和调节时间。此处可参考胡寿松的《自动控制原理》: 
ξ越大,衰减震荡过程受到的阻尼越大,对波形的影响如上图。
注意:
1.带宽最好取速度环带宽的10%到20%,阻尼比取在0.707到1之间。
2.就笔者仿真结果来看,锁相环参数主要影响观测器阶跃响应曲线的波形和曲线的平滑程度,对电角度的相位滞后产生的影响极小。
3.观测器是否能成功观测速度信号,观测出的角度和实际角度之间的误差大小主要取决于观测器反馈系数矩阵。
4.设计参数时应该优先确定好龙伯格观测器的反馈系数矩阵,待观测器能正常使用后再细调锁相环参数来得到一个较好的响应信号波形。
这篇关于电机控制学习之路:simulink仿真之龙伯格观测器+锁相环的参数设计的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






