基于滑模观测器的永磁同步电机无位置传感器控制

1、传统滑膜观测器设计

目前,大多数传统SMO算法的设计是基于静止坐标系下的数学模型的，重写电机的电压方程为：
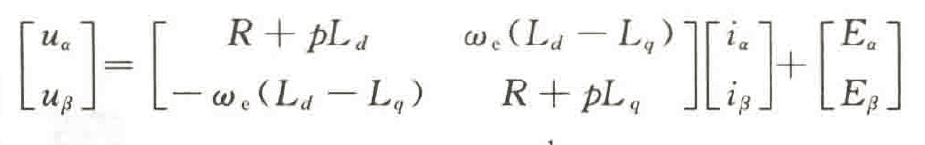其中：Ld|、Lq为定子电感；we为电角速度；p=d/dt,为微分算子；Uα、Uβ为定子电压，iα，iβ为定子电流，Eα，Eβ为扩展反电动势（EMF），且满足：

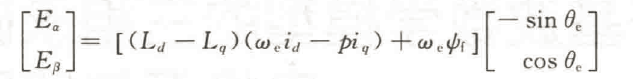
对于表贴式三相PMSM(Ld=Lq=L,) ,打展反电动势的表达式（2）将被间化，为仅与电机的转速有关的变量。当转速较快时,反电动势较大,反之亦然。对于内置式三相PMSM(L.≠L。)而言,从式（2）可知:扩展反电动势的大小除了与电机的转速有关外,还与定子电流is和定子电流i。的微分pig有关,这意味着电机的负载状态将影响扩展反电动势的大小。当电机运行在高速重载条件下时,定子电流具有较大的变化,从而成为扩展反电动势畸变的重要成分。
由于内置式三相PMSM的扩展反电动势包含电机转子位置和转速的全部信息，所以只有准确获取扩展反电动势,才可以解算出电机的转速和位置信息。为便于应用SMO来观测扩展反电动势,将式（1）的电压方程改写为电流的状态方程形式:


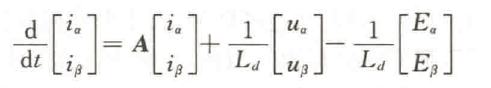
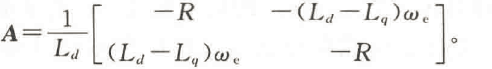
为了获得扩展反电动势的估计值,传统SMO的设计通常如下

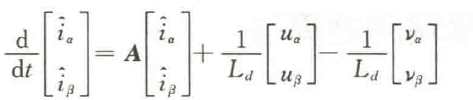
其中:iα，iβ为定子电流的观测值;uα、uβ为观测器的控制输入。
设计滑模控制律：

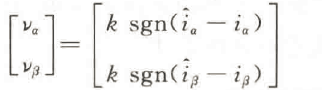
当观测器的状态变量达到滑模面i。=0、ig=0之后,观测器状态将一直保持在滑模面上。根据滑模控制的等效控制原理,此时的控制量可看作等效控制量,可得

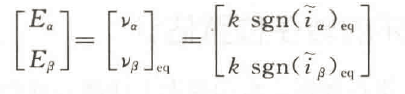
2、基于反正切函数的转子位置估计

由于实际的控制量是-一个不连续的高频切换信号,为了提取连续的扩展反电动势估计值,通常需要外加一个低通滤波器,即

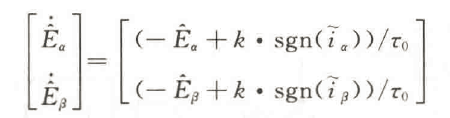
然而,对等效控制量进行低通滤波处理时，在高频切换信号滤除的同时,扩展反电动势的估计值将发生幅值和相位的变化。通常,为了获得转子位置信息,可通过反正切函数方法获得，即

通过式（8）滤波处理获得的反电动势估算分量会引发相位延迟，该延迟将直.接影响转子位置的估算准确性,较小的滤波截止频率将引发较大的相位延迟。在实际应用中为解决该问题,通常需要在式（9）计算出转子位置的基础上再加上一个角度补偿,用来弥补由于低通滤波器的延迟效应所造成的位置角度估算误差，即

其中:w。为低通滤波器的截止频率。
为了获得转速信息，可以对式(5- 10)进行求微分运算。特别地,对于表贴式三相PMSM，此时转速估计值的表达式为

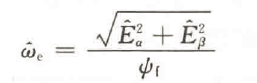
综上所述，传统SMO算法的实现原理如图

综上所述,基于SMO的三相PMSM无传感器控制框图如图所示：

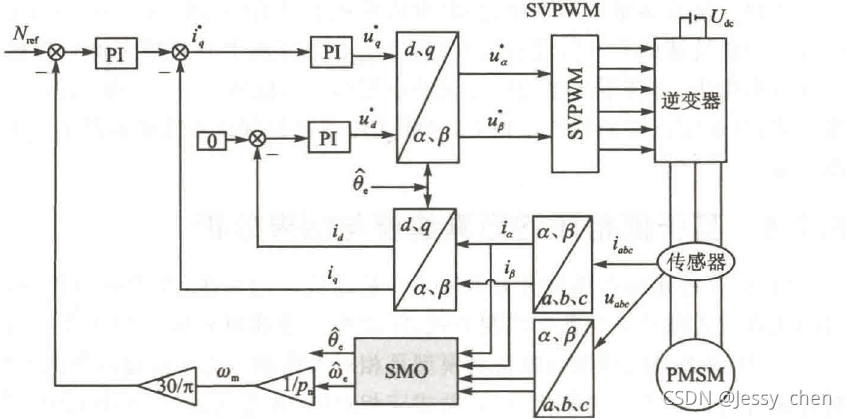
3、simulink仿真实现及模块介绍

上图是总的框图，仿真时间为0.4s。

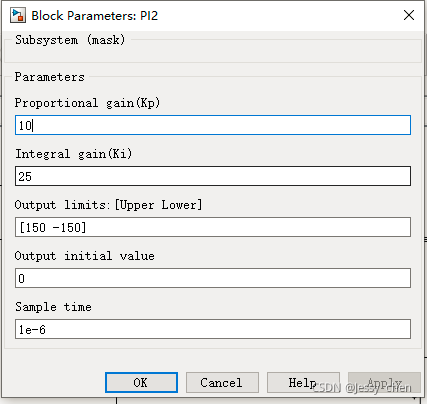
3.1、速度环

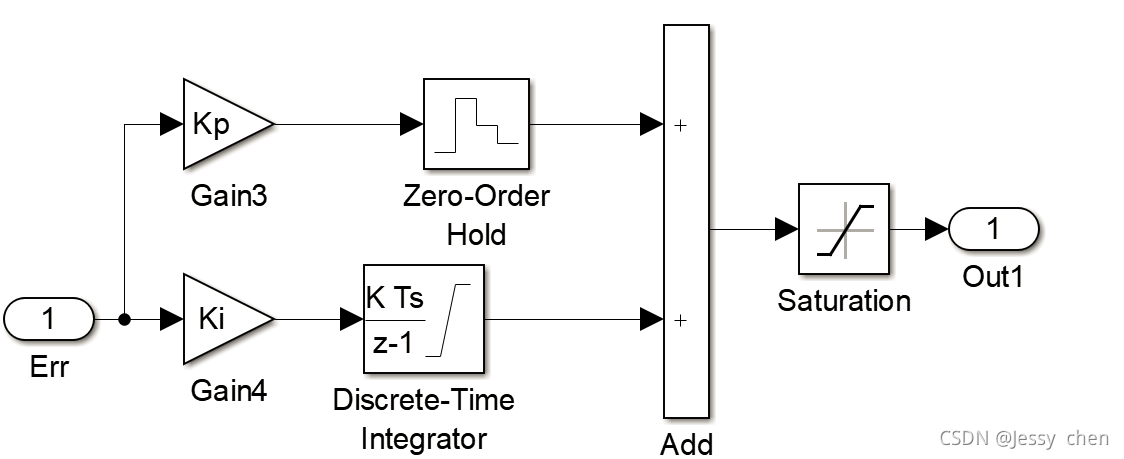
3.2、电流环（Id和Iq一样）

3.3、SVPWM

PWM开关频率为5kHZ，母线电压为311V
仿真框图不做介绍

3.4、universal bridge(逆变器)

3.5、Three-Phase V-I Measurement

Voltage measurement必须要是phase-to-ground。

3.6、PMSM（永磁同步电机）

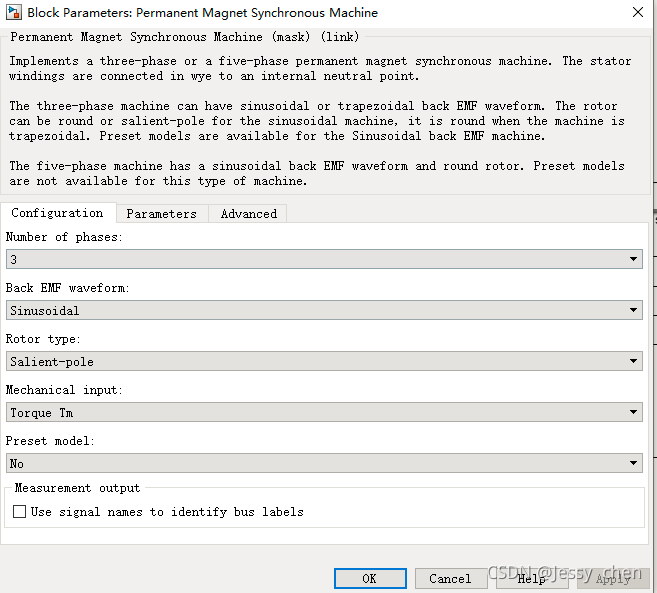
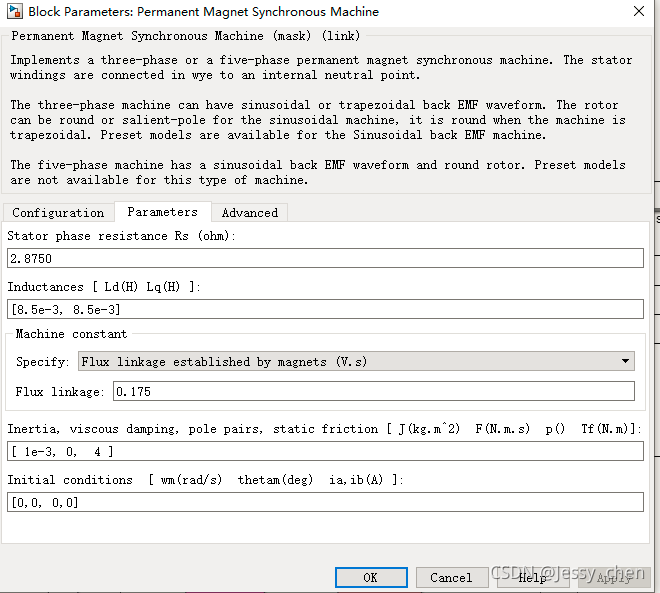
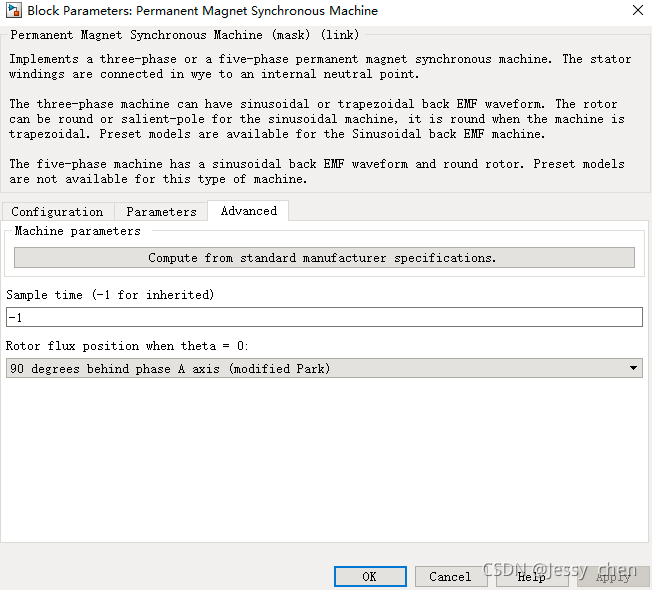
3.7、mod模块（取余）

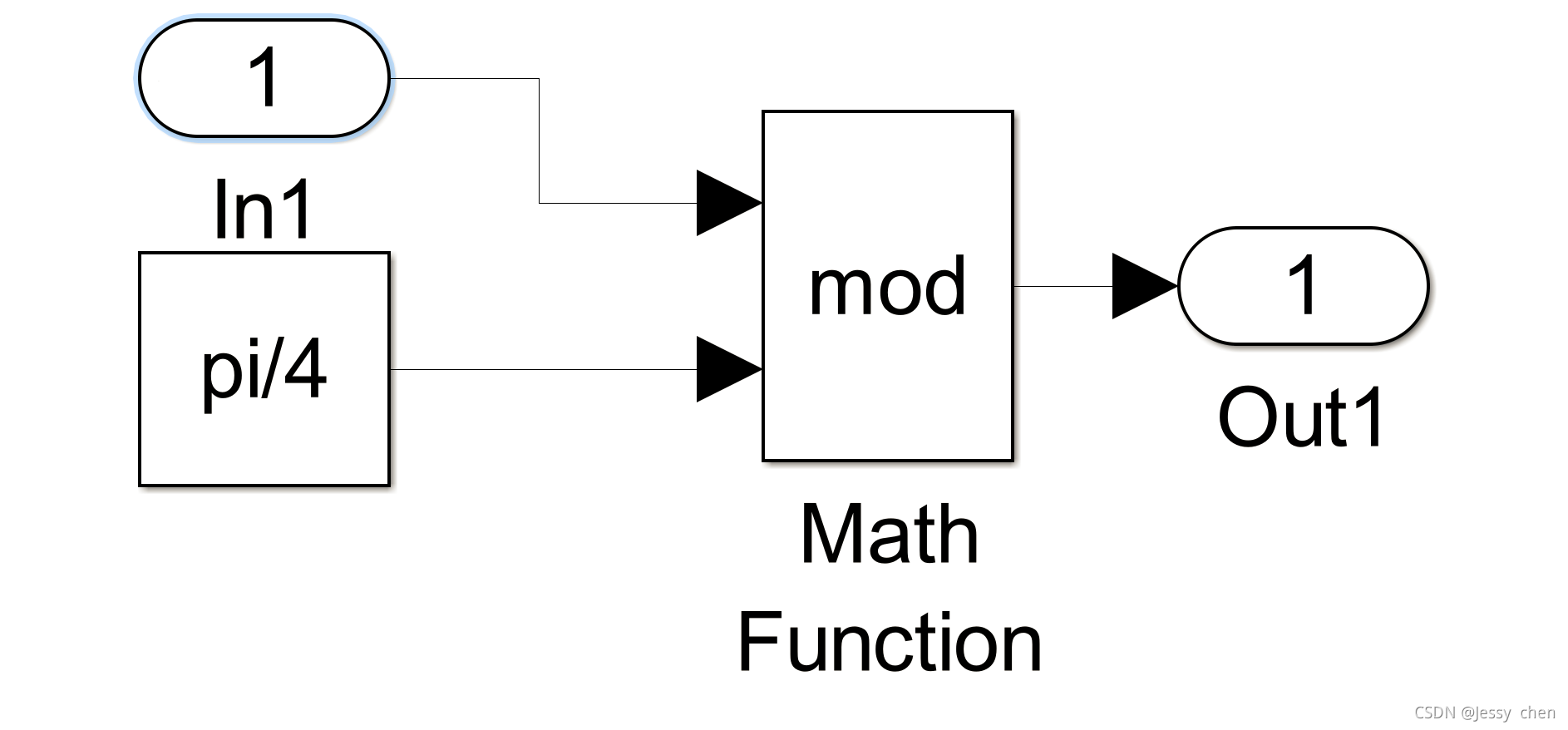
3.8、SMO模块（滑模控制）

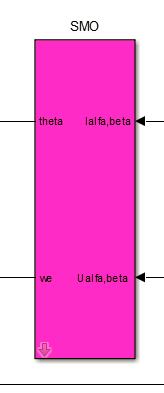
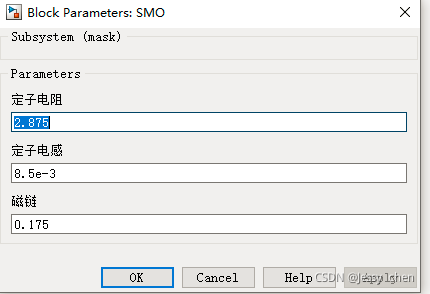
SMO模块
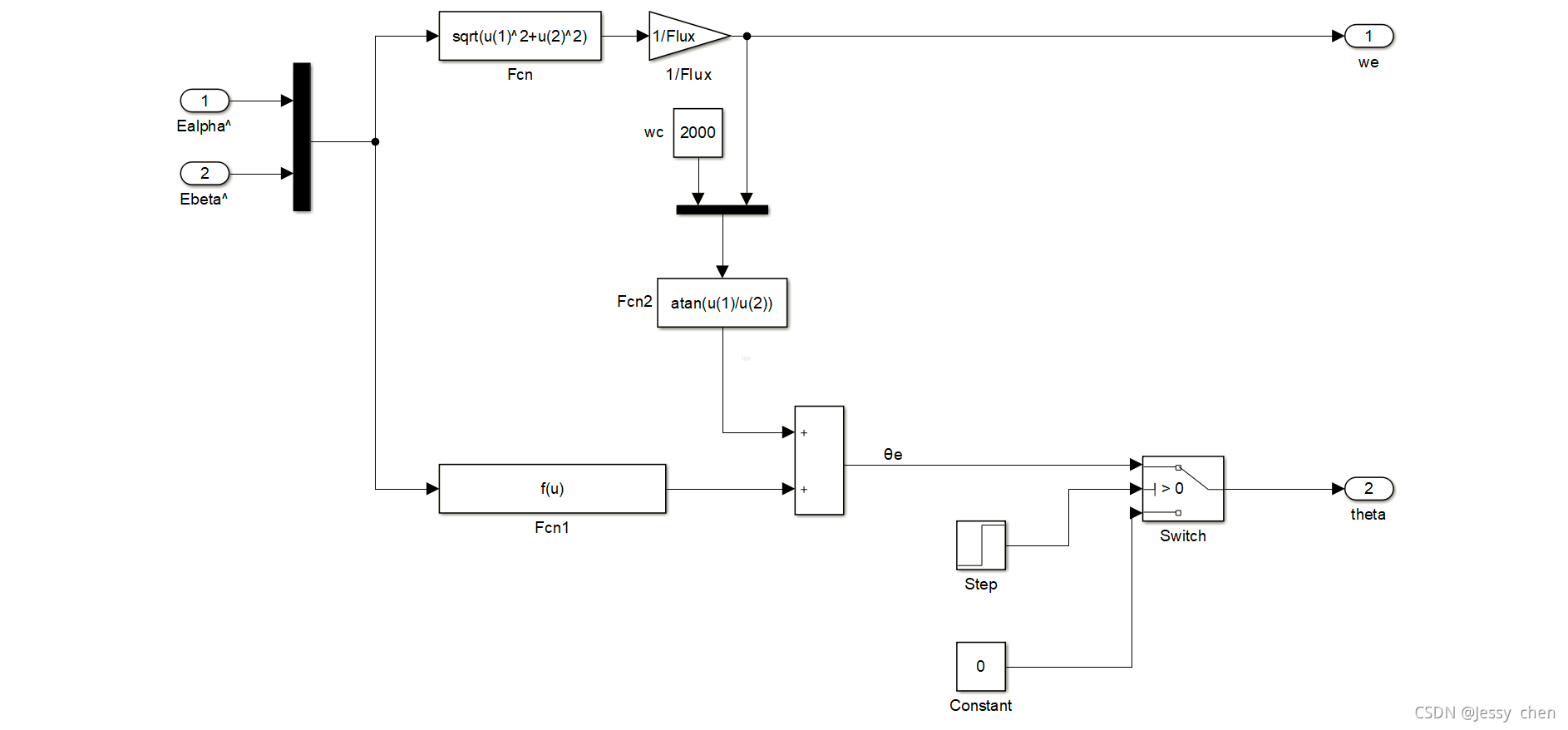
arctan-function模块

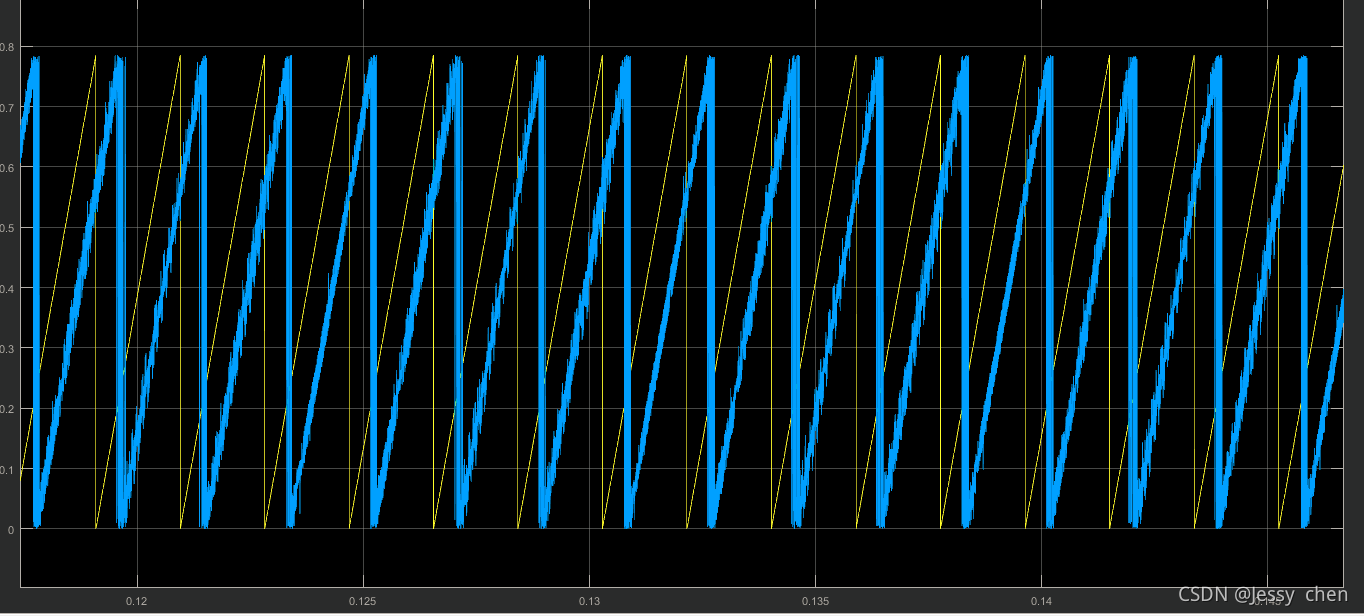
3.9转子实际位置与估计位置仿真图

3.10、转子实际位置与估计位置的误差

3.11、实际转速与估计转速的仿真

3.12、实际转速与估计转速的误差

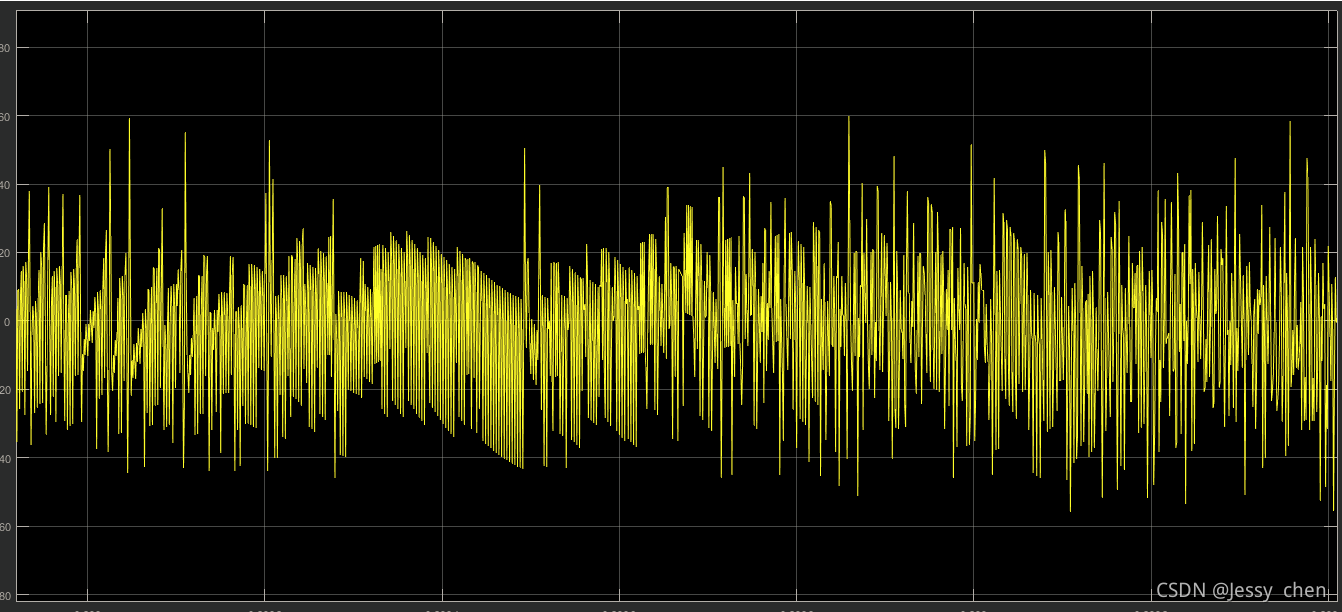
4、总结

由上图可以看出基于这种算法的效果不是很好，其他文献有改进算法，有兴趣的小伙伴可以交流一下

点赞啦！！！！！