本文主要是介绍观测器与卡尔曼滤波器的状态估计对比,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在实时控制系统和信号处理中,观测器和卡尔曼滤波器是两个常用于状态估计的工具。本文将通过 Matlab 演示这两者在一维运动系统中的应用,并深入探讨它们的概念、核心点、异同以及本质。
观测器与卡尔曼滤波器的概念
观测器
观测器是一种用于估计系统状态的机制。通过测量系统的输出和输入,观测器可以估计系统的状态,即使系统的状态无法直接观测。观测器的本质是通过对系统行为的监测,利用系统的动态模型来估计状态。
卡尔曼滤波器
卡尔曼滤波器是一种递归滤波器,用于对系统状态进行估计。它结合了系统的动态模型和实际测量的信息,通过优化估计过程中的协方差,提供对系统状态的最优估计。
核心点
观测器的核心
观测器的核心是设计一种机制,通过测量输出和输入,使系统状态的估计能够收敛到真实的系统状态。观测器通常不需要系统的动态模型,更关注对测量的处理和状态估计的收敛性。
卡尔曼滤波器的核心
卡尔曼滤波器的核心在于结合了系统的动态模型和测量信息,通过递归地更新状态估计和协方差矩阵,提供对系统状态的最优估计。卡尔曼滤波器对系统的动态性能和噪声的建模非常重要。
异同对比
相似之处
- 观测器和卡尔曼滤波器都用于系统状态的估计,通过测量和模型信息来推断系统的未知状态。
- 两者都具有实时更新的能力,可以根据新的测量数据和输入进行即时的状态估计。
不同之处
- 观测器通常关注系统状态可测但测量不完全的情况,而卡尔曼滤波器更适用于需要考虑系统动态和噪声的状态估计问题。
- 滤波器更注重噪声的处理,采用卡尔曼滤波器等方法来优化对系统状态的估计,考虑观测噪声和系统噪声。
Matlab演示对比
% 初始化
x_true = 0;
v_process = 0.1;
n_measurement = 10; % 增大测量噪声,突出卡尔曼滤波器优势% 观测器初始化
x_observer = 0;
observer_estimates = [];% 卡尔曼滤波器初始化
A = 1;
H = 1;
Q = v_process^2;
R = n_measurement^2;
x_kalman = 0;
P_kalman = 1;
kalman_estimates = [];% 模拟运动
for k = 1:50x_true = x_true + v_process * randn();y_measurement = x_true + n_measurement * randn();% 观测器更新x_observer = x_observer + 0.1 * (y_measurement - x_observer);observer_estimates = [observer_estimates, x_observer];% 卡尔曼滤波器更新x_kalman = A * x_kalman;P_kalman = A^2 * P_kalman + Q;K = P_kalman * H / (H^2 * P_kalman + R);x_kalman = x_kalman + K * (y_measurement - H * x_kalman);P_kalman = (1 - K * H) * P_kalman;kalman_estimates = [kalman_estimates, x_kalman];
end% 绘制图表
figure;
plot(1:50, observer_estimates, '-o', 'DisplayName', 'Observer Estimates');
hold on;
plot(1:50, kalman_estimates, '-s', 'DisplayName', 'Kalman Filter Estimates');
plot(1:50, x_true * ones(1,50), '--', 'DisplayName', 'True State');
hold off;
title('Comparison of Observer and Kalman Filter Estimates');
xlabel('Time Steps');
ylabel('State Estimates');
legend('Observer', 'Kalman Filter', 'True State');
grid on;
n_measurement = 5;

n_measurement = 10;
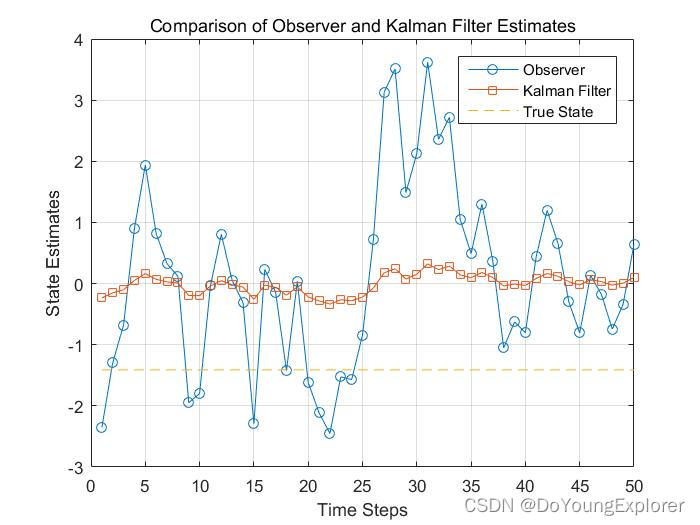
通过对比图表,我们可以清晰地看到观测器和卡尔曼滤波器在状态估计中的不同表现。观测器虽然能够跟踪系统的变化,但卡尔曼滤波器通过更复杂的模型和对噪声的优化处理,提供了更准确的状态估计。
这篇关于观测器与卡尔曼滤波器的状态估计对比的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


