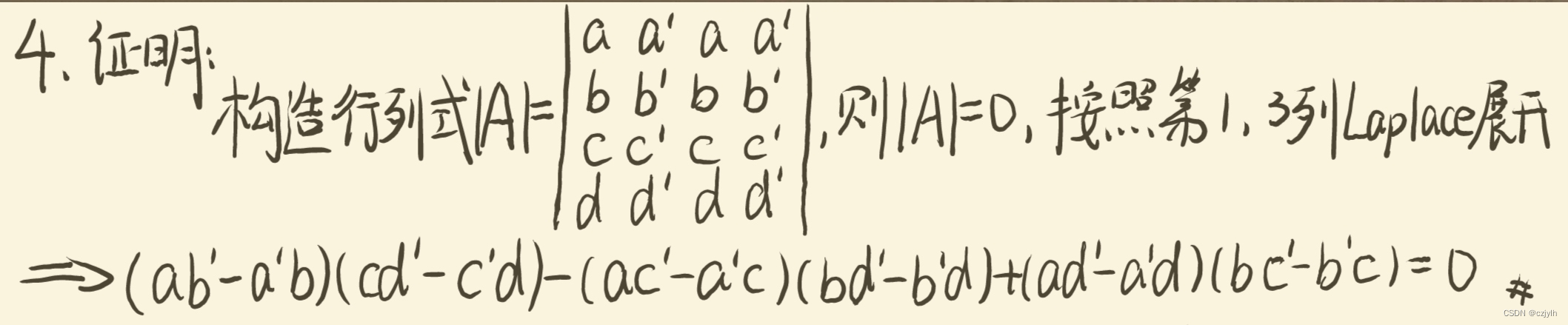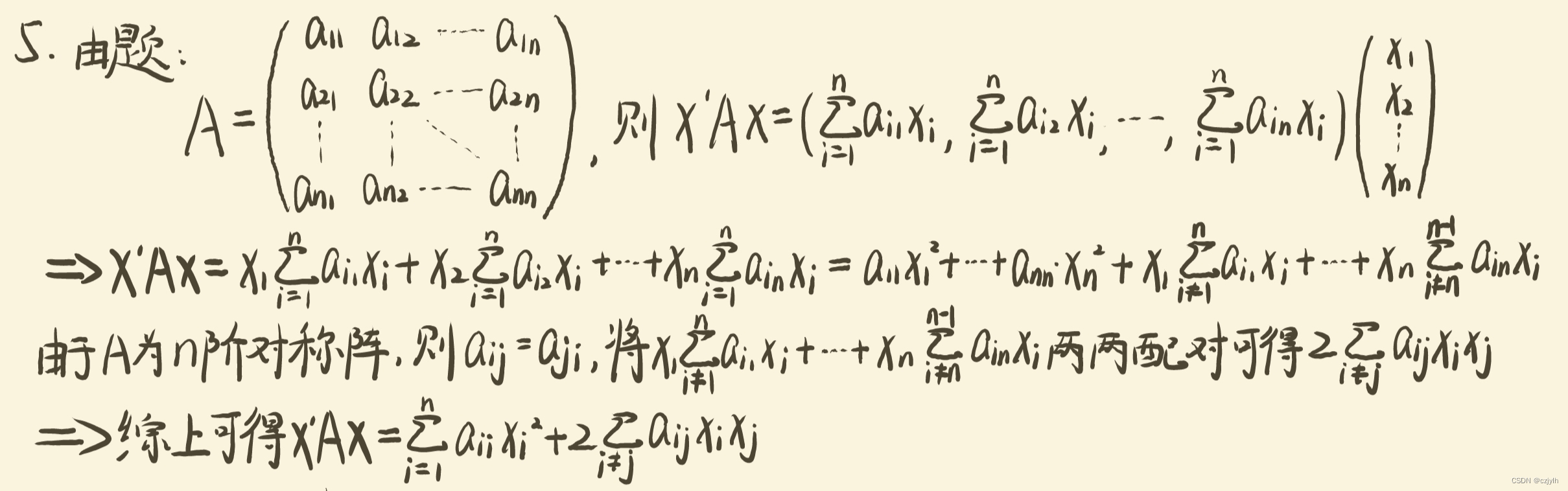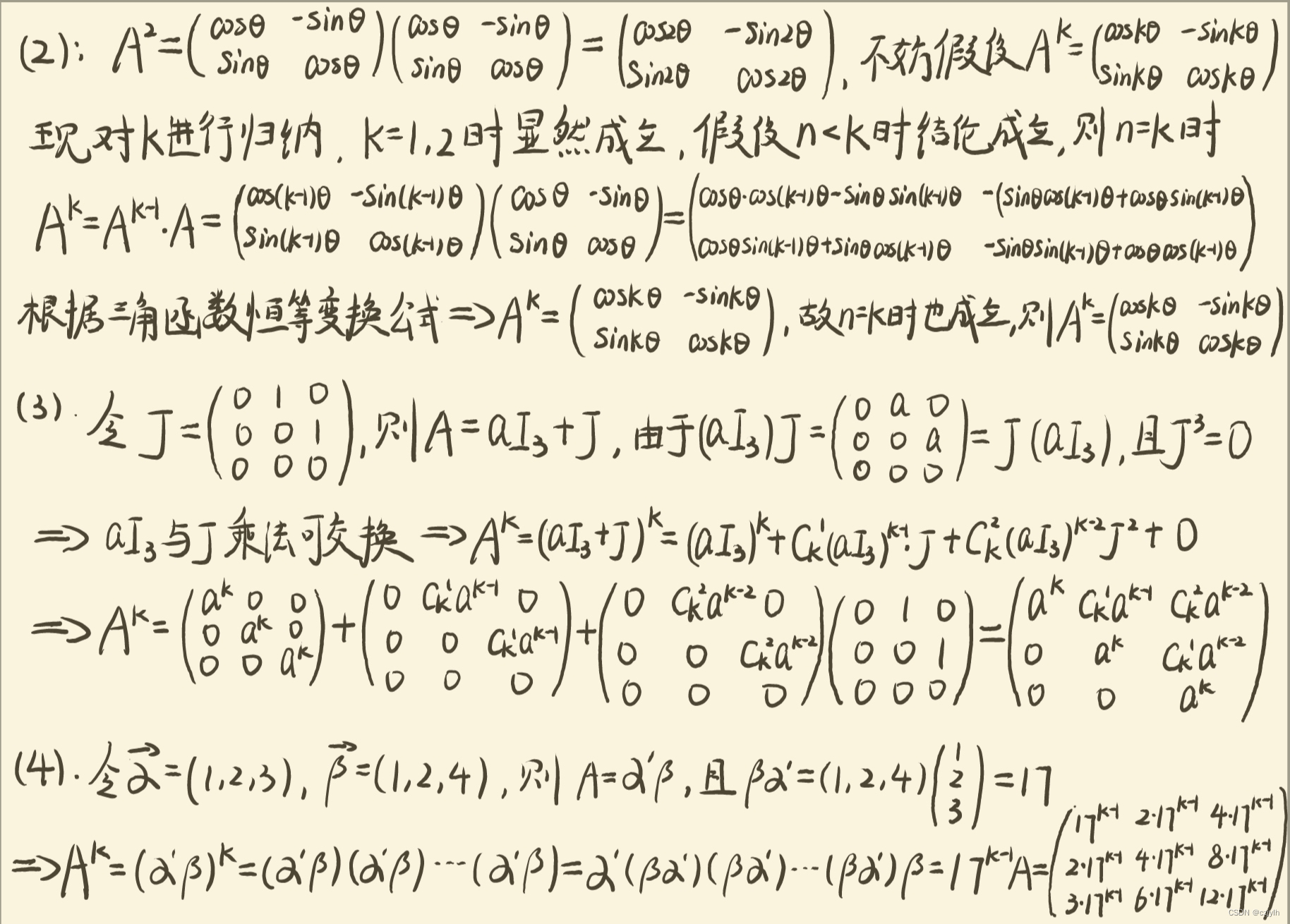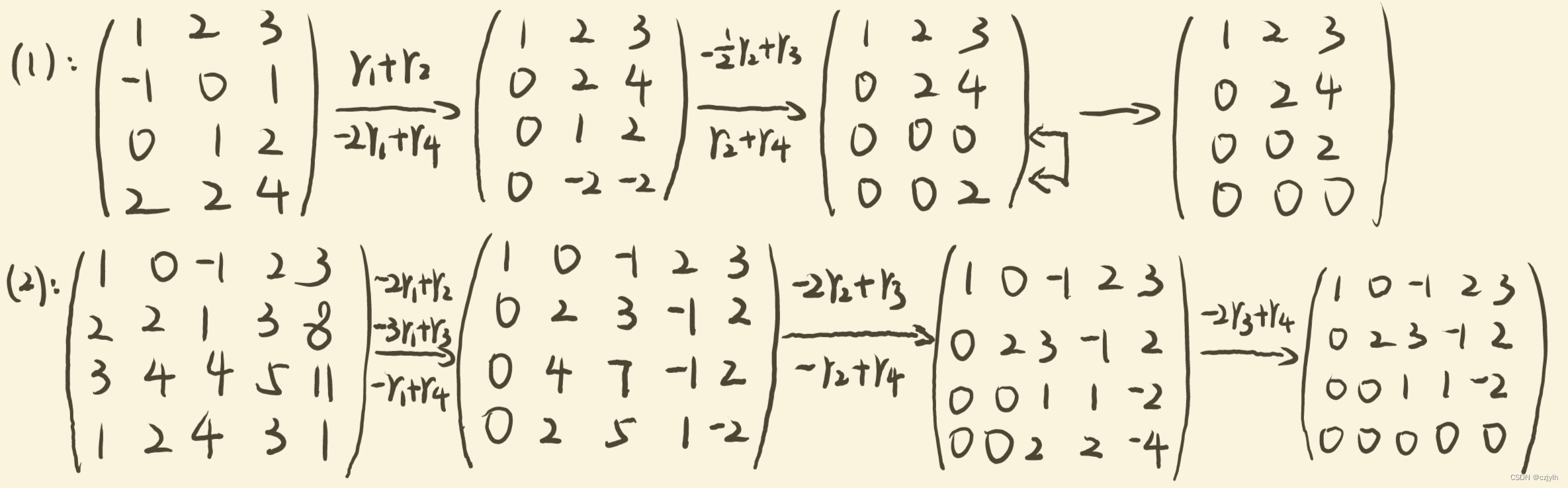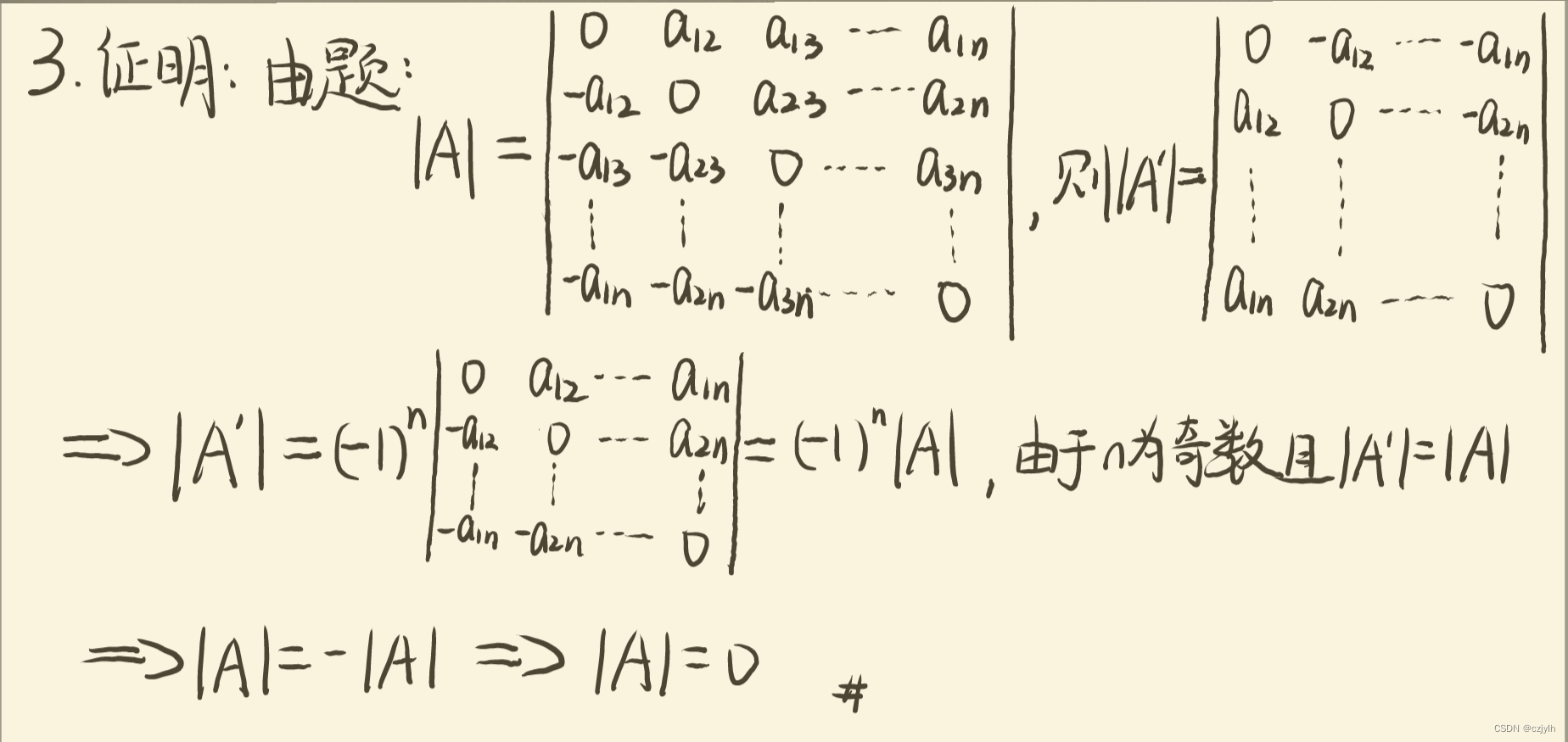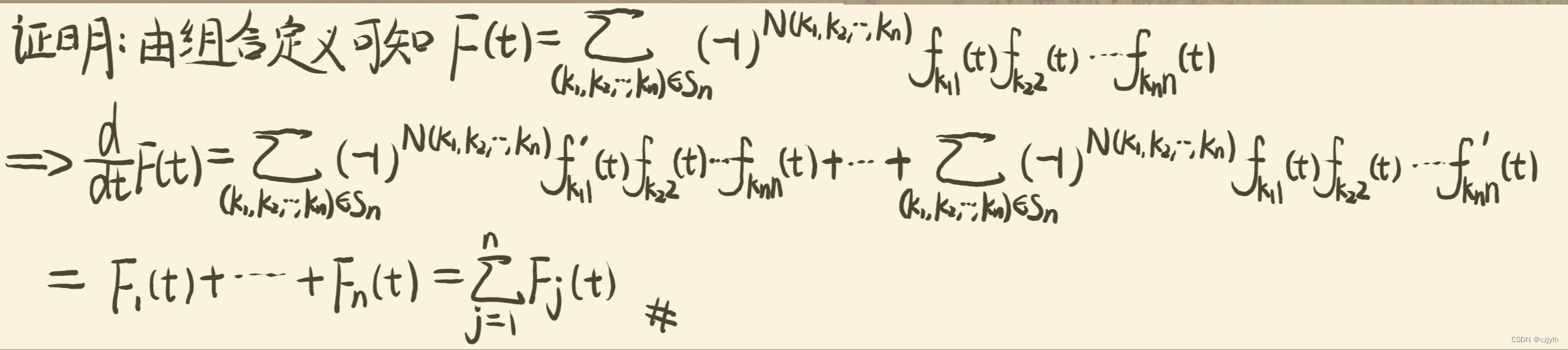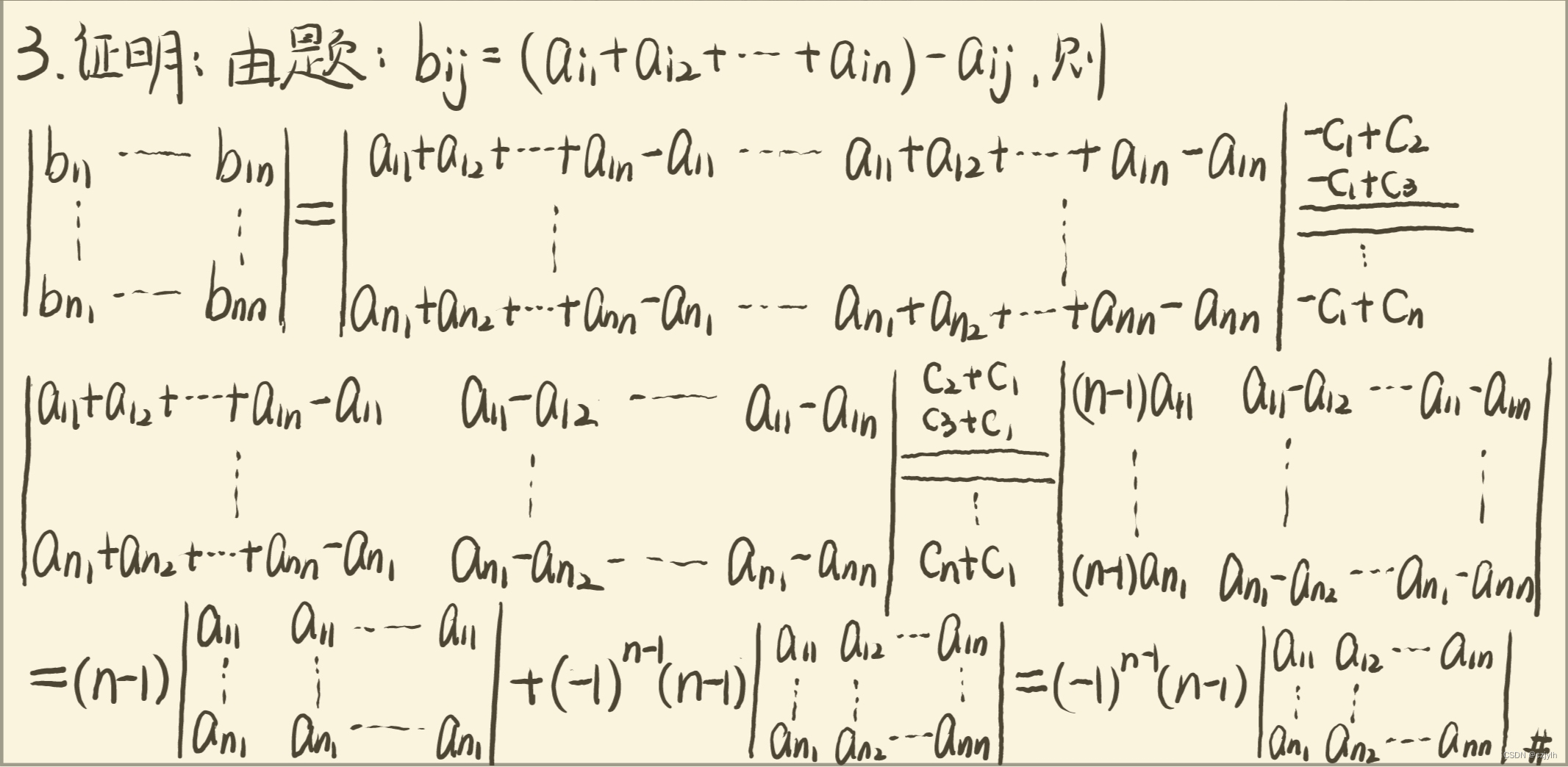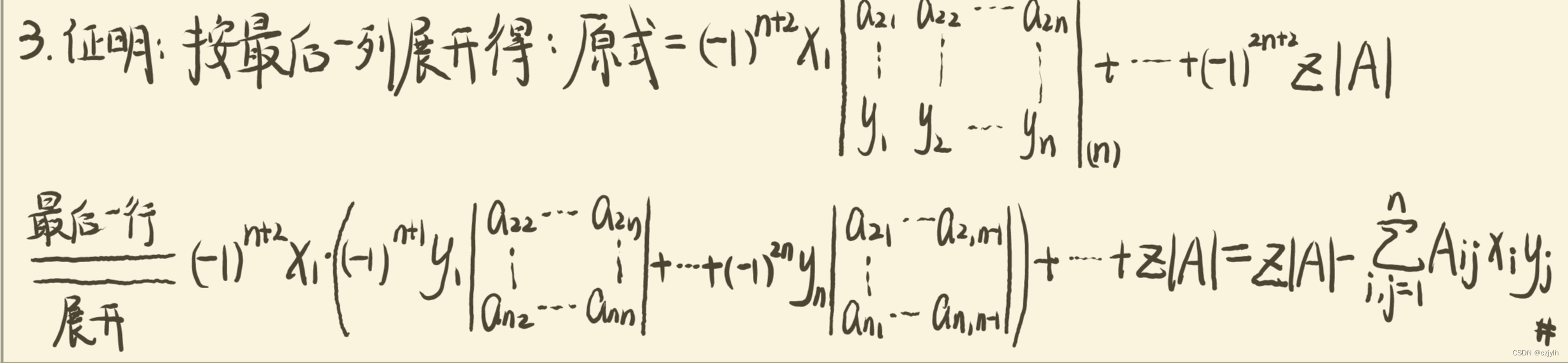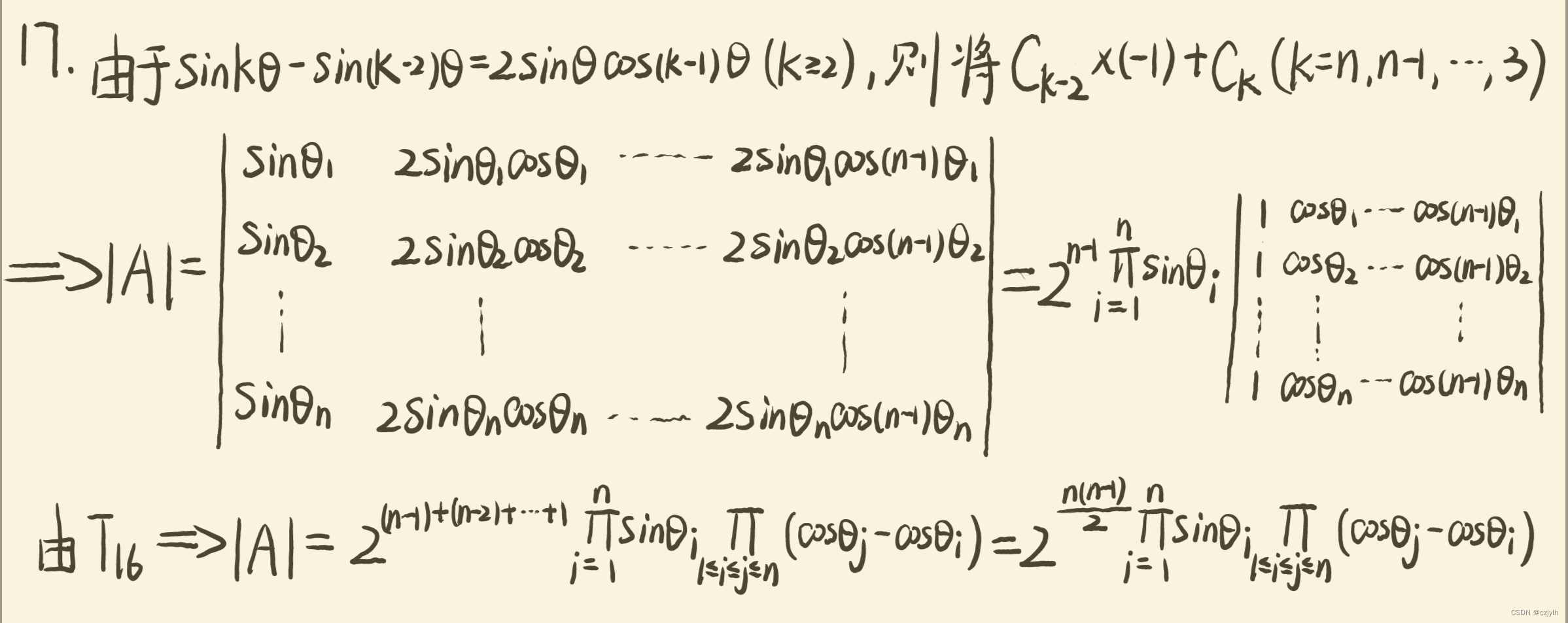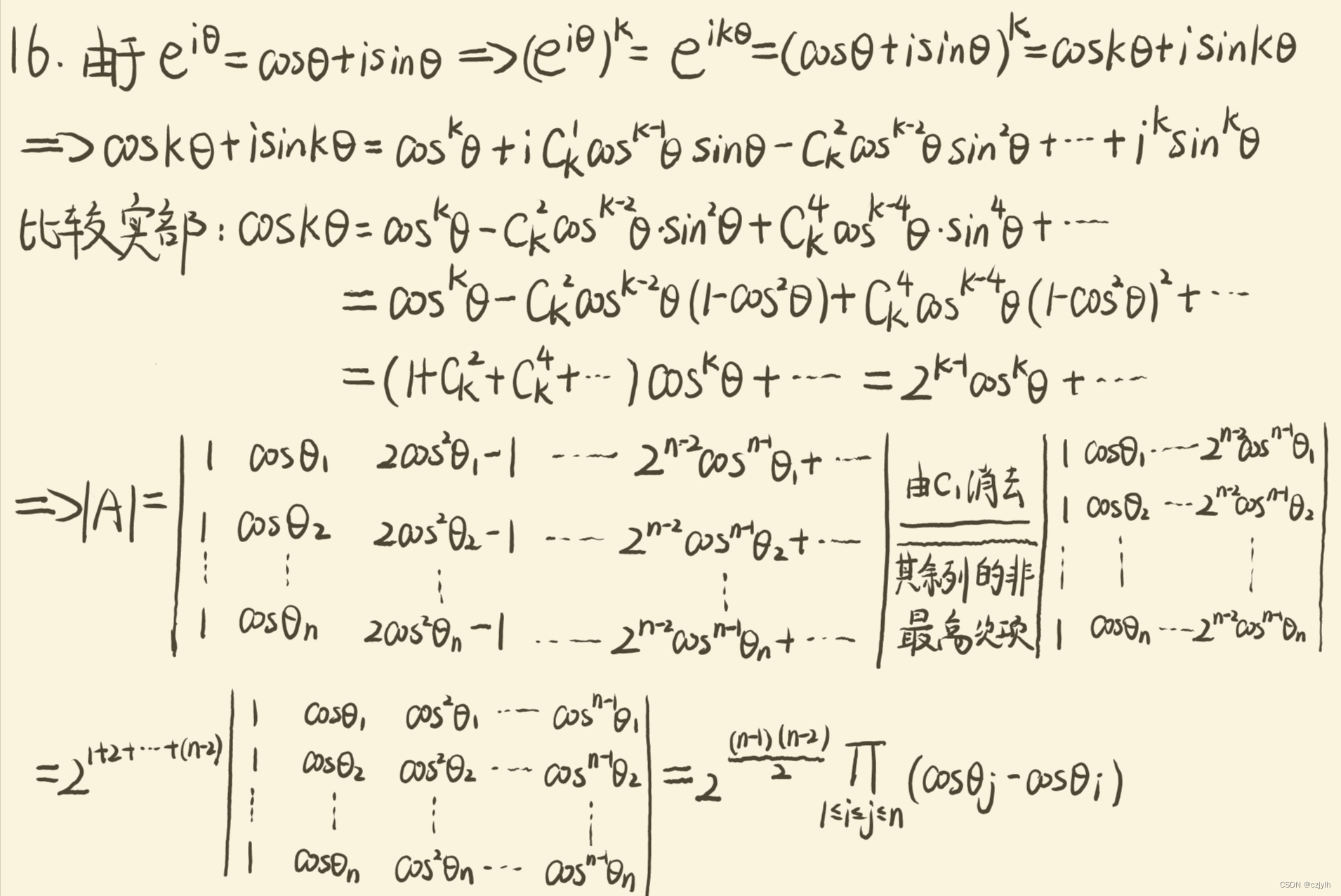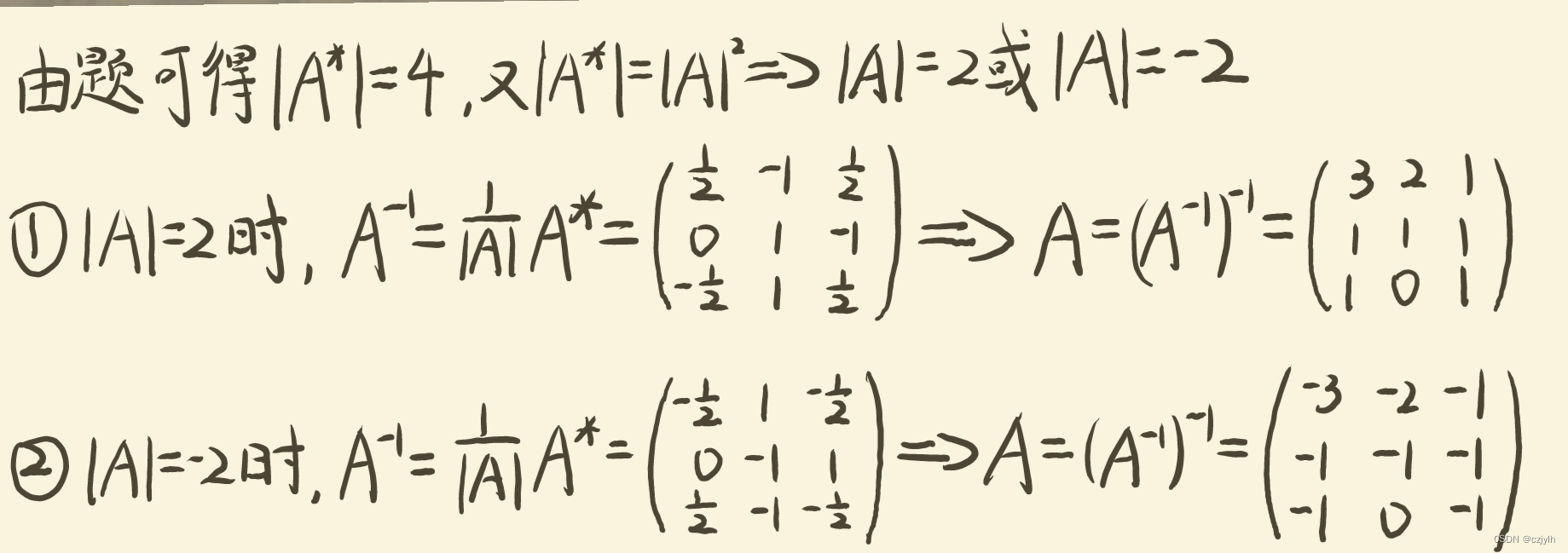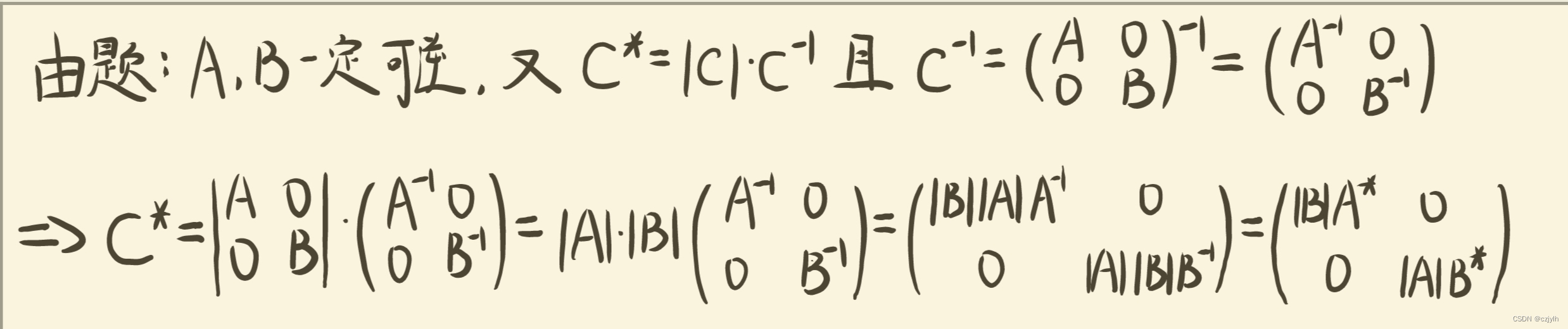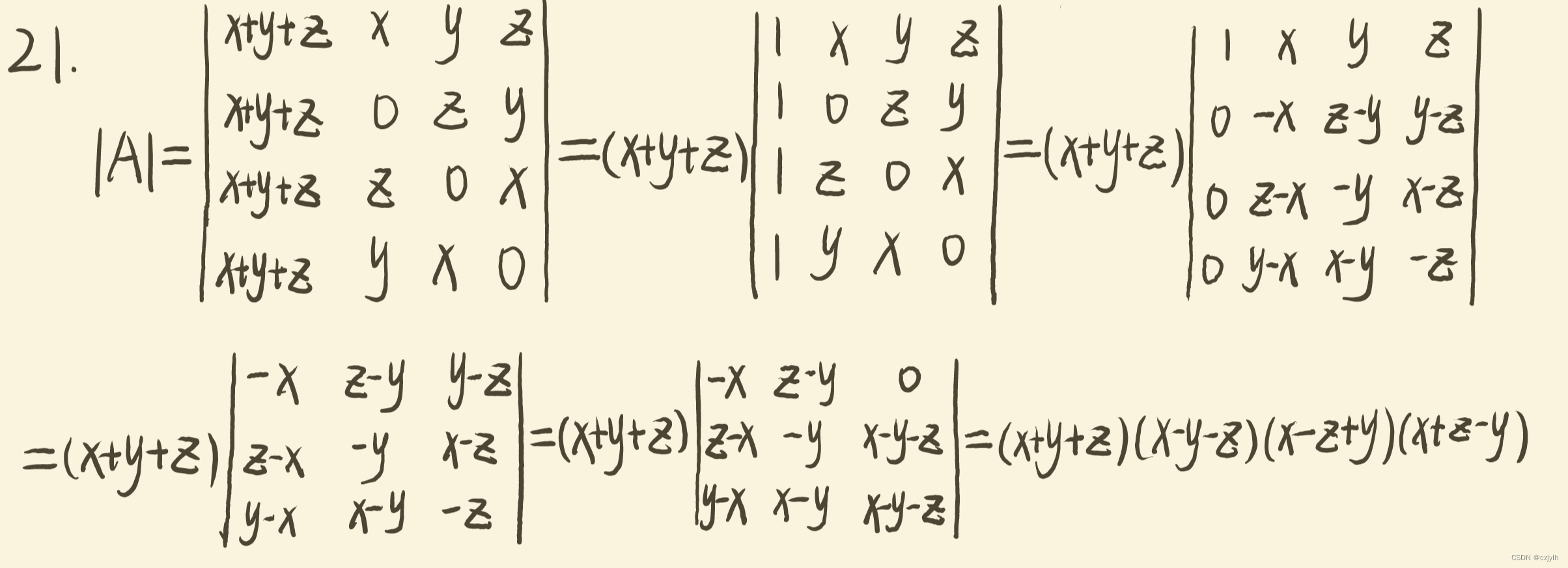绿皮专题
高代绿皮第四版课后习题1.7 T4
原题 利用行列式及Laplace定理,证明下列恒等式: 解析 思路: 根据需证明的式子构造行列式如下 由于 中第1,3列相同,故 再按照第1,3列进行Laplace展开即可证得结论 参考解题细节:
高代绿皮第四版课后习题1.4 T3
原题 证明: 当n为奇数时,n阶反对称行列式值等于0 解析 思路: 根据反对称行列式的定义可知 不妨记 为n阶反对称行列式, 为 的转置 则有 又n为奇数且 故有 即 参考解题细节:
高代绿皮第四版课后习题1.5 T5
原题 设 是次数不超过 n-2 的多项式,求证: 对 均有 解析 思路: 由题干条件可知 都是单项式 的线性组合 不妨令 利用上式将所求行列式中的 展开可发现 行列式有n列但只有n-1个单项式 则将其拆分后的每个行列式中一定至少有两列共用同一个单项式或只差一个系数 故这些行列式必有两列成比例,即恒等于0,即证原命题 参考解题细节:
高代绿皮第四版课后习题1.5 T6
原题 设 t 是一个参数, 求证: 其中 是 在 中的代数余子式 解析 思路: 将 的第一列拆分得 将第二个行列式的第一列乘以(-1)分别加到剩下n-1列上可得 再将其按照第一列展开可得 同理将上述第一个行列式进行同理拆分即可证得结论 参考解题细节:
高代绿皮第四版课后习题1.6 T6
原题 设 其中 是未知数, 为常数,求证: 是一个最高次项为1的n次多项式,且其n-1次项系数为 解析 思路: 将 的第一列进行拆分可得 再将两个行列式拆分并分别计算其n-1次项系数后进行累加即得结论 参考解题细节:
高代绿皮第四版课后习题1.6 T4
原题 若一个n阶行列式中零元素的个数超过 个,证明: 这个行列式的值为0 解析 思路: 由于n阶行列式共有 个元素,若零元素个数大于 个,则非零元素至多为 个 但n阶行列式有n行n列,故可知 中至少有一个为0 根据行列式的组合定义可得 参考解题细节:
高代绿皮第四版课后习题复习题一T25
原题 设n阶行列式 , 是元素 的代数余子式,求证: 解析 思路: 见下参考过程与高代绿皮第四版课后习题1.5 T6-CSDN博客 参考解题细节:
高代绿皮第四版课后习题复习题一T7
原题 求证:n阶行列式 解析 思路: 首先将第 元素 拆分为 ,则根据行列式性质可分为两个新的行列式 再将第一个行列式定义为 ,第二个行列式按第一列展开可得 记原式为 ,则有 接着将 按第一列展开可得递推式 处理二阶递推式的一般方法为特征方程法 故可令 则特征方程为 易得其两解为 接下来再分别讨论两解相同与否的情况即可证得结
高代绿皮第四版课后习题复习题一 T3
原题 设 是一个n阶行列式, 是它的第 元素的代数余子式,求证: 解析 思路: 将原行列式按最后一列展开得到新的n+1个行列式,再将这前n个新行列式按最后一行展开即证结论 参考解题细节:
高代绿皮第四版课后习题复习题一T17
原题 计算下列行列式的值 解析 思路1: 利用棣莫弗公式与二项式展开对比虚部系数得到 的表达式,具体类似操作见 高代绿皮第四版课后习题复习题一T16-CSDN博客 思路2: 根据积化和差公式 故可从后向前依次将 利用积化和差公式化简得可提出每行每列的公因式 于是 其中 为高代绿皮第四版课后习题复习题一T16-CSDN博客中的行列式,即可求解
高代绿皮第四版课后习题复习题一T16
原题 计算下列行列式的值 解析 思路: 利用复变函数中的欧拉公式 再由棣莫弗公式可知 由二项式展开公式可得 提取出其实部 故有 于是可以利用此公式将 中第3至第n列元素进行展开 最后用第一列消去其余列的非最高次项后再提出后n-2列的公因式 注意到最后变成了Vandermonde行列式,运用公式求解即可 参考解题细节:
高代绿皮第四版课后习题复习题一T11
原题 设n阶行列式 求证: 解析 思路: 利用数学归纳法 首先验证n=1与n=2的情况是否成立,易证成立 现假设对 时结论成立,下证 的情形 记 ,按最后一列展开即得递推式 由归纳假设可知 满足结论,故只需将其代入上述递推式中进行化简即可证得 参考解题细节:
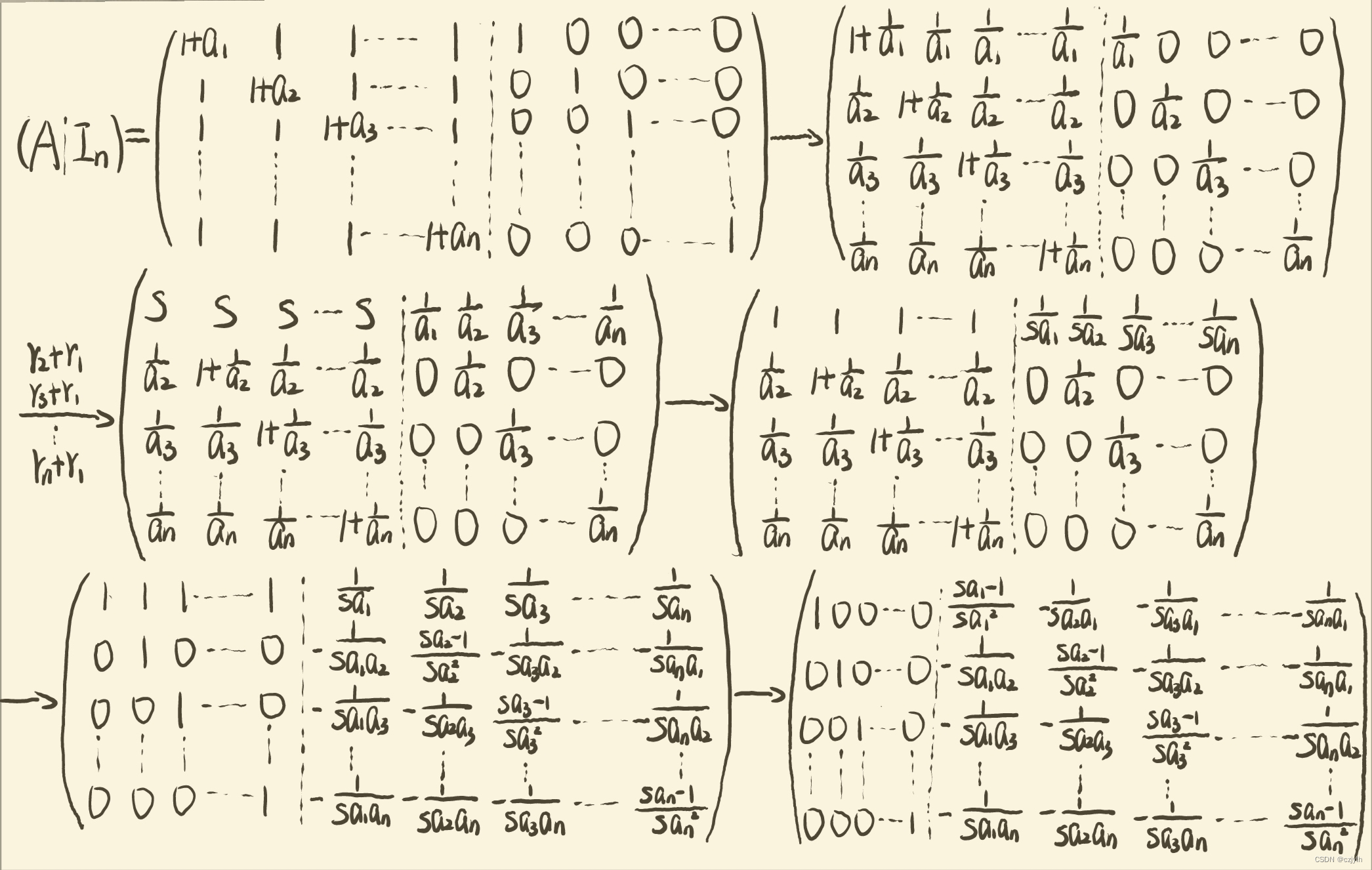
高代绿皮第四版课后习题复习题二 T24
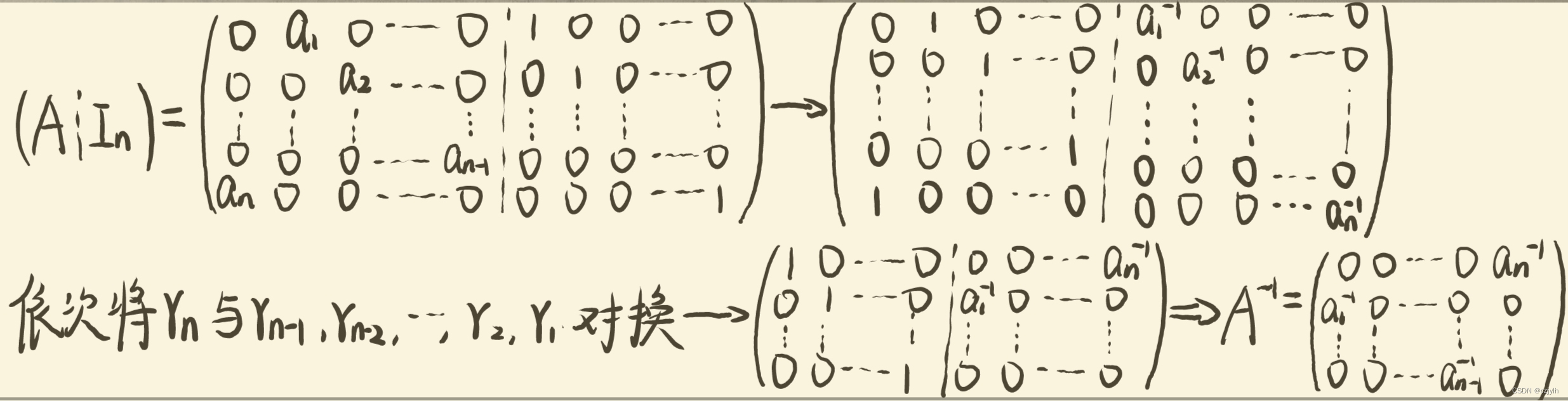
原题 已知 试求 解析 思路: 首先由公式求出 的值,即 再利用伴随矩阵与逆矩阵的关系公式求出逆矩阵,即 最后根据 与 的关系求出 ,即 参考解题细节:
高代绿皮第四版课后习题复习题一T19
原题 计算下列n阶行列式的值 解析 思路: 注意到 与标准的Vandermonde行列式缺少了 i 次幂的列,故可构造n+1阶Vandermonde行列式 即 将 按第n+1行展开得 由于 则只需求出 的系数,由于 为Vandermonde行列式,根据公式求得 根据多项式知识可得 的系数为 于是 故求得 参考解题细节:
高代绿皮第四版课后习题复习题一T21
原题 计算行列式的值 解析 思路: 注意到每行元素之和均相同,故可将后三列元素全部加到第一列上并提出公因式 接着将第一列中后三行元素消去并按第一列展开,按照三阶行列式进行公式展开化简即可 参考解题细节: