高代绿皮第四版课后习题复习题一T16

2024-02-26 20:10

文章标签 第四版复习题习题课后 t16 高代绿皮

本文主要是介绍高代绿皮第四版课后习题复习题一T16，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原题

计算下列行列式的值

$|A|=\left| \begin{matrix} 1 & \cos {{\theta }_{1}} & \cos 2{{\theta }_{1}} & \cdots & \cos (n-1){{\theta }_{1}} \\ 1 & \cos {{\theta }_{2}} & \cos 2{{\theta }_{2}} & \cdots & \cos (n-1){{\theta }_{2}} \\ \vdots & \vdots & \vdots & {} & \vdots \\ 1 & \cos {{\theta }_{n}} & \cos 2{{\theta }_{n}} & \cdots & \cos (n-1){{\theta }_{n}} \\ \end{matrix} \right|$

解析

思路:

利用复变函数中的欧拉公式

$e^{i\theta}=\cos{\theta}+i\sin{\theta}$

再由棣莫弗公式可知

$e^{ik\theta}=(\cos{\theta}+i\sin{\theta})^{k}=\cos{k\theta}+i\sin{k\theta}$

由二项式展开公式可得

$LHS=\cos^{k}{\theta}+iC_{k}^{1}\cos^{k-1}{\theta}\sin{\theta}+i^{2}C_{k}^{2}\cos^{k-2}{\theta}\sin^{2}{\theta}+\cdots+i^{k}\sin^{k}{\theta}$

提取出其实部

$\begin{aligned}\Re(LHS)&= \cos^{k}{\theta}-C_{k}^{2}\cos^{k-2}{\theta}\sin^{2}{\theta}+C_{k}^{4}\cos^{k-4}{\theta}\sin^{4}{\theta}+\cdots\vspace{2ex}\\&=\cos^{k}{\theta}-C_{k}^{2}\cos^{k-2}{\theta}(1-cos^{2}{\theta})+\cdots\vspace{2ex}\\&=(1+C_{k}^{2}+C_{k}^{4}+\cdots) \cos^{k}{\theta}+\cdots\vspace{2ex}\\&=2^{k-1}\cos^{k}{\theta}+\cdots \end{aligned}$

故有

$\cos{k\theta}=\Re(LHS)=2^{k-1}\cos^{k}{\theta}+\cdots$

于是可以利用此公式将 $|A|$ 中第3至第n列元素进行展开

最后用第一列消去其余列的非最高次项后再提出后n-2列的公因式 $2^{k-2}\,(k=3,4,\cdots,n)$

注意到最后变成了Vandermonde行列式,运用公式求解即可

参考解题细节:

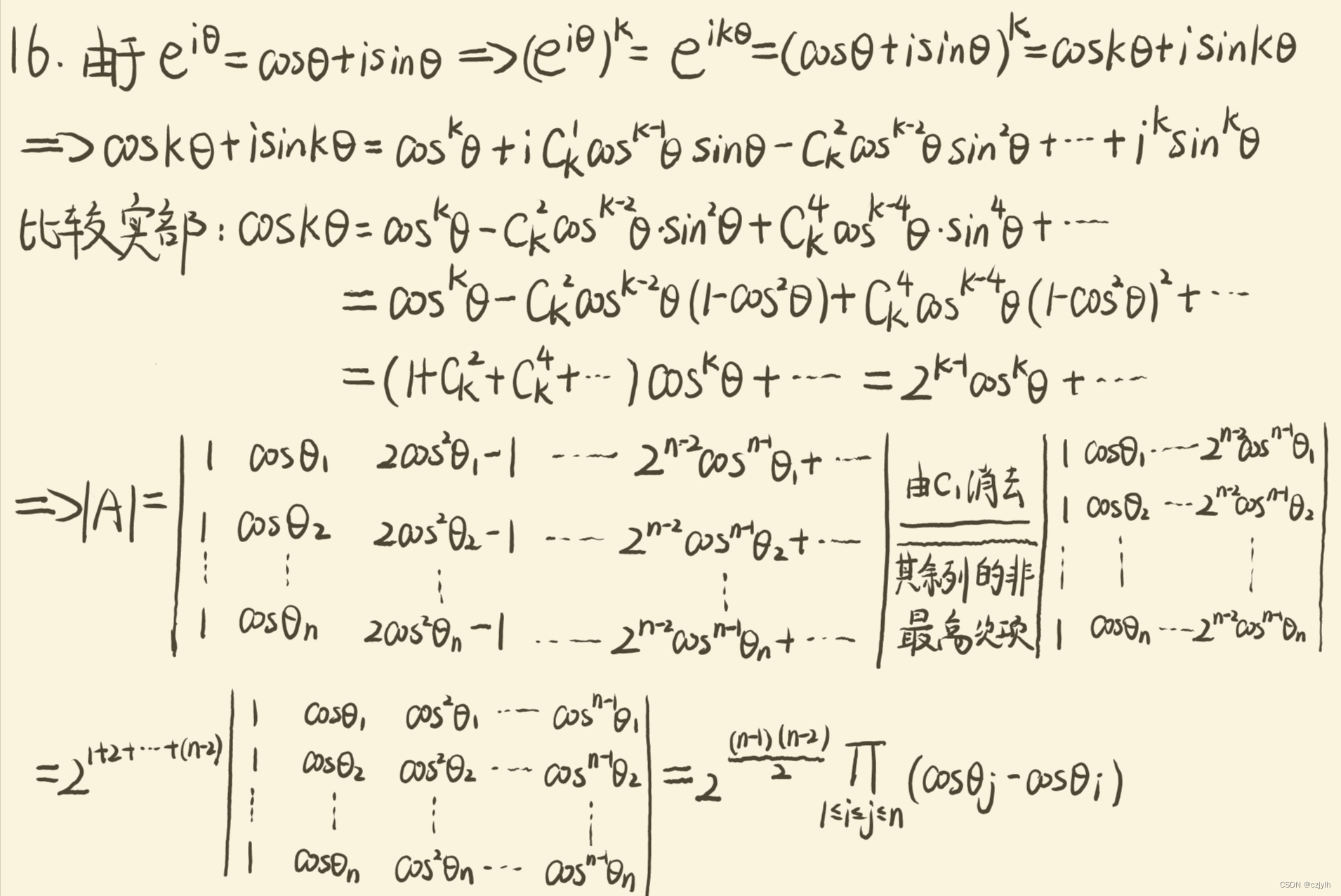
这篇关于高代绿皮第四版课后习题复习题一T16的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/750010。 23002807@qq.com

相关文章

【C++ Primer Plus习题】13.4

【C++ Primer Plus习题】13.4

大家好,这里是国中之林! ❥前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。有兴趣的可以点点进去看看← 问题: 解答: main.cpp #include <iostream>#include "port.h"int main() {Port p1;Port p2("Abc", "Bcc", 30);std::cout <<

阅读更多...

第六章习题11.输出以下图形

第六章习题11.输出以下图形

🌏个人博客：尹蓝锐的博客希望文章能够给到初学的你一些启发～如果觉得文章对你有帮助的话，点赞 + 关注+ 收藏支持一下笔者吧～ 1、题目要求：输出以下图形

阅读更多...

【C++ Primer Plus习题】12.2

【C++ Primer Plus习题】12.2

大家好,这里是国中之林! ❥前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。有兴趣的可以点点进去看看← 问题: 解答: main.cpp #include <iostream>#include "String.h"using namespace std;int main(){String s1(" and I am a

阅读更多...

c++习题30-求10000以内N的阶乘

c++习题30-求10000以内N的阶乘

目录一，题目二，思路三，代码一，题目描述求10000以内n的阶乘。输入描述只有一行输入，整数n（0≤n≤10000）。输出描述一行，即n!的值。用例输入 1 4 用例输出 1 24 二，思路 n n! 0 1 1 1*1=1 2 1*2=2 3 2*3=6 4

阅读更多...

读Spring实战（第四版）概括—装配Bean

读Spring实战（第四版）概括—装配Bean

很久很久以前读过Spring实战（第三版），因为第三版和第四部差异还是特别明显的，在整体思想上有了比较重大的改变，比如用注解和JavaConfig替换Xml以及现在非常火热的Springboot在书的最后也有提到。OK，开始看书，书本的第一章讲了一下Spring存在的目的（简化Java开发）和Spring的功能，以及Spring3->Spring4增加了哪些功能，那我就从第二章开始概括本书，以给我

阅读更多...

C语言程序与设计第四版课后习题 - 1~8章大合集

C语言程序与设计第四版课后习题 - 1~8章大合集

前言本文章是一个大合集，按照课后习题的命名方式命名，方便寻找，只需要在目录上点相对应的题号即可在这里插入图片描述第一章课后习题 1.1 编写一个C程序题目概述：请参照本章例题，编写一个C程序，输出一下信息： *****************************Very good!***************************** 代码实现： #define

阅读更多...

【C++ Primer Plus习题】12.1

【C++ Primer Plus习题】12.1

大家好,这里是国中之林! ❥前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。有兴趣的可以点点进去看看← 问题: 解答: main.cpp #include <iostream>#include "Cow.h"using namespace std;int main(){Cow c1;Cow c2("老母牛", "喝奶"

阅读更多...

应届生入职练手习题-蒙特卡洛算法(1.5H)

应届生入职练手习题-蒙特卡洛算法(1.5H)

应届生入职练手习题 [编辑] 模拟射击，根据命中概率来求PI 要求：假设有一个半径为1000的圆形靶子（具体单位没有意义，不用写），我们随意对其进行射击，那么，统计所有落在圆形外接正方形中的弹着点，可以很容易得知：命中这个圆形靶子的概率是圆形的面积与外接方形面积的比目的：检验编程风格和实现效率要解这个题目就得有对蒙特卡洛算法的了解，原理如下在数值积分法中，利用求单位圆的1/4的面积

阅读更多...

《C Primer Plus》第10 章复习题和编程练习

《C Primer Plus》第10 章复习题和编程练习

目录一、复习题二、编程练习一、复习题 1. 下面的程序将打印什么内容？ #include <stdio.h>int main(){int ref[] = {8, 4, 0 ,2};int *ptr;int index;for (index = 0, ptr = ref; index < 4; index++, ptr++){printf("%d %d\n", ref[in

阅读更多...

软考-软件设计师（UML习题）

软考-软件设计师（UML习题）

💝💝💝欢迎来到我的博客，很高兴能够在这里和您见面！希望您在这里可以感受到一份轻松愉快的氛围，不仅可以获得有趣的内容和知识，也可以畅所欲言、分享您的想法和见解。非常期待和您一起在这个小小的网络世界里共同探索、学习和成长。💝💝💝 ✨✨ 欢迎订阅本专栏 ✨✨ 前言小郑正在备考2024年下半年的中级软件设计师，所以打算开展一个软考备考专栏，在这里记录一下备

阅读更多...