牛顿专题
点云配准之ICP和NDT算法的高斯牛顿法求解
ICP算法 NDT算法 代码:https://github.com/taifyang/pointcloud-registration 参考:高翔《自动驾驶与机器人中的SLAM技术》
【机器人学导论】6自由度机械臂逆运动学求解—牛顿法(数值法,仅旋转关节)
我以前是机器人专业,不过学的不多,教程应该是灰色封面的《机器人学导论》。3年前学的了,软件仿真学的是ABB,上手操作是KUKA的机器人。本文是给别人解决问题的记录,写个笔记。代码是matlab的,不免费分享,但是看我的解析应该也能自己写出来。我不从事这个行业,很多东西已经模糊了。 文章目录 一、DH参数二、正向运动学三、逆向运动学3.1 逆向运动学的求解方法:3.11 解析法(Ana
5、梯度下降法,牛顿法,高斯-牛顿迭代法
1、梯度下降 2、牛顿法 3、高斯-牛顿迭代法 4、代码部分 1.梯度下降法代码 批量梯度下降法c++代码: /*需要参数为theta:theta0,theta1目标函数:y=theta0*x0+theta1*x1;*/#include <iostream>using namespace std;int main()
数学基础 -- 牛顿法
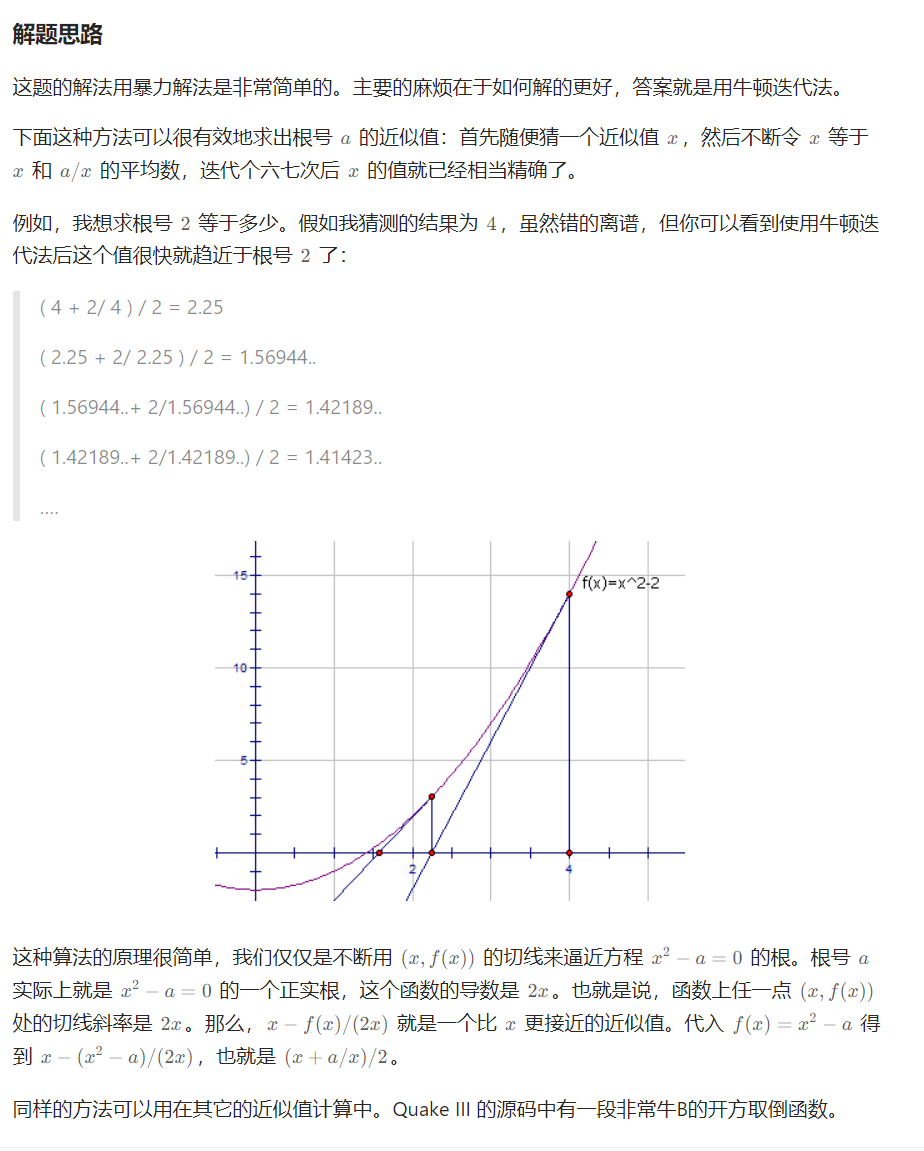
牛顿法 牛顿法是一种迭代法,用来寻找函数的根(即找到 f ( x ) = 0 f(x) = 0 f(x)=0 的解)。它的基础是泰勒展开,通过利用函数的一阶导数信息,牛顿法能够快速逼近根。 牛顿法的推导 假设我们要找到函数 f ( x ) f(x) f(x) 的根,也就是求解方程 f ( x ) = 0 f(x) = 0 f(x)=0。从一个初始猜测 x 0 x_0 x0 开始,我
数学建模学习(118):牛顿冷却定律的原理解析、案例分析与Python求解
介绍来源:2020全国大学生数学建模竞赛论文展示(A070) ,这里我们详细完整的对该优秀论文的方法进行学习和实践。 文章目录 1. 牛顿冷却定律的定义2. 牛顿冷却定律公式3. 牛顿冷却定律的推导4. 牛顿冷却定律的应用方法5. 牛顿冷却定律的验证6. 牛顿冷却定律的图形7. 案例一7.1 题目7.2 推导求解7.3 Python 求解 8. 案例二8.1 题目8.2 推导求解8.3 P
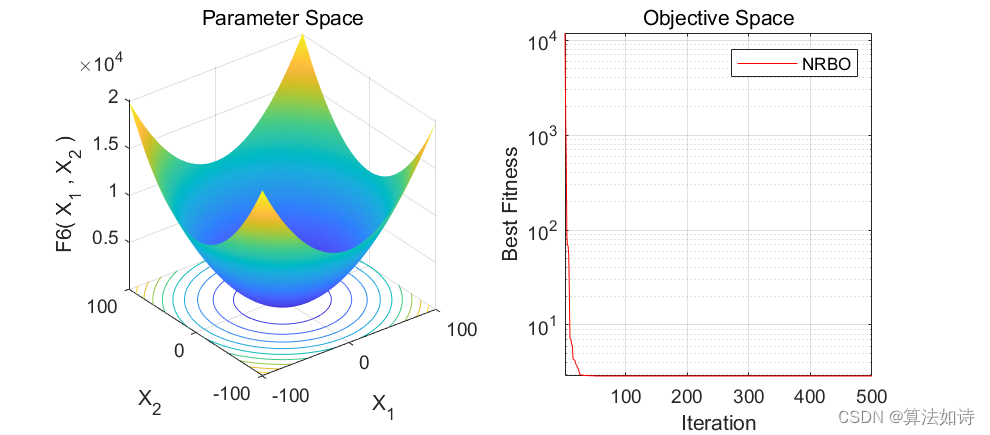
2024年中科院SCI期刊牛顿-拉夫逊优化算法NRBO优化Transformer-LST模型的多变量时间序列预测
matlab R2024a以上 一、数据集 二、2024年中科院SCI期刊牛顿-拉夫逊优化算法NRBO 牛顿-拉夫逊优化算法(Newton-Raphson-based optimizer, NBRO)是一种新型的元启发式算法(智能优化算法),该成果由Sowmya等人于2024年2月发表在中科院2区Top SCI期刊《Engineering Applications of
C语言 | 使用牛顿法求非线性方程的一个实根(附代码)
========================================== 博主github:https://github.com/MichaelBeechan 博主CSDN:https://blog.csdn.net/u011344545 ==========================================
matlab实现牛顿迭代法求解非线性方程组
已知非线性方程组如下 3*x1-cos(x2*x3)-1/2=0 x1^2-81*(x2+0.1)^2+sin(x3)+1.06=0 exp(-x1*x2)+20*x3+(10*pi-3)/3=0 求解要求精度达到0.00001 ---------------------------------------------------------分--割--线------------
机器学习的基础算法--牛顿法
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。 把非线性函数 在 处展开成泰勒级数,取其线性部分,作为非线性方程的近似方程, 则有 设 ,则其解为 因为这是利用泰勒公式的一阶展开, ,这里并不是完全相等,而是近似相等,即去掉泰勒级数2级以上的项,这里求得的 并
C++实现牛顿迭代法求解f(x)=0
#include <iostream> #include <cmath> using namespace std; #define f(x) x*x - 8 #define df(x) 2*x double EPS = 1e-6; double Newton(double xFirst) { double xSecond; int iteCount = 0;//迭代次数
非线性优化:高斯-牛顿法的原理与实现
非线性优化:高斯-牛顿法的原理与实现 引言 在实际应用中,很多问题都是非线性的。非线性优化问题广泛应用于机器学习、数据拟合、工程设计等领域。高斯-牛顿法是一种常用于解决非线性最小二乘问题的迭代算法。本文将详细介绍高斯-牛顿法的原理、推导过程,并通过Python代码实现该算法。 高斯-牛顿法原理 问题定义 非线性最小二乘问题可以表示为: min x ∑ i = 1 m [ r i (
线性/非线性最小二乘 与 牛顿/高斯牛顿/LM 原理及算法
最小二乘分为线性最小二乘和非线性最小二乘 最小二乘目标函数都是min ||f(x)||2 若f(x) = ax + b,就是线性最小二乘;若f(x) = ax2 + b / ax2 + bx 之类的,就是非线性最小二乘; 1. 求解线性最小二乘 【参考】 2. 求解非线性最小二乘 需要用到牛顿法,高斯牛顿法,或者LM法 目标函数都是min F(x) = min ||f(x)||2
修正牛顿法求解无约束问题
function [x,val,k]=revisenm(fun,gfun, Hess, x0) %功能:用修正牛顿法求解无约束问题:min f(x) %输入:x0是初始点,fun, gfun,Hess分别是求目标函数值,梯度,Hesse矩阵的函数 %输出:x,val分别是近似最优点和最优值,k是迭代次数 n=length(x0);maxk=150; rho=0.55;sigma=0.4;t
超分辨率重建——梯度下降、坐标下降、牛顿迭代
在阅读相关文献的时候,经常会遇到梯度下降,坐标下降,牛顿迭代这样的术语,今天把他们的概念整理一下。 梯度下降 整理自百度 梯度下降法是一个最优化算法,通常也称为最速下降法。 顾名思义,梯度下降法的计算过程就是沿梯度下降的方向求解极小值(也可以沿梯度上升方向求解极大值)。 其迭代公式为 ,其中 代表梯度负方向, 表示梯度方向上的搜索步长。梯度方向我们可以通过对
HDU2899 Strange fuction(牛顿迭代法)
最近刚学完数值分析上的方程求根——牛顿法,所以做几题练习一下。 Problem Description Now, here is a fuction: F(x) = 6 * x^7+8*x^6+7*x^3+5*x^2-y*x (0 <= x <=100) Can you find the minimum value when x is between 0 and 100.
“高引用”《牛顿传》重版再出,今晚八点,来直播间“遇见牛顿”!
“现在,我要演示世界体系的框架。” "I now demonstrate the frame of the system of the world." 他是伟人,亦是怪人 THE SAVIOUR AND PRISONER 万有引力定律、运动定律、微积分、光学、二项式定理……你如今在中学课本中学到的数学和物理知识,有多少是出自这位“百科全书式”天才之手? - 诗人亚历山大·蒲柏说他颠覆了统治
[机器学习必知必会]牛顿法和拟牛顿法
前言 同梯度下降法一样,牛顿法和拟牛顿法也是求解无约束最优化问题的常用方法。牛顿法本身属于迭代算法,每一步需要求解目标函数的海赛矩阵的逆矩阵,计算比较复杂。拟牛顿法通过正定矩阵近似海赛矩阵的逆矩阵或海赛矩阵,简化了这一计算过程。 需要提前了解的知识 泰勒展开 当 f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0处具有 n n n阶连续导数,我们可以用 x −
牛顿迭代法的可视化详解
来源:DeepHub IMBA本文约1800字,建议阅读10分钟本文利用可视化方法,为你直观地解析牛顿迭代法。 牛顿迭代法(Newton's method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。 以 Isaac Newton 和 Joseph Raphson 命名的 Newton-R
历时30年探索牛顿之谜,中国科学家测出迄今最高精度万有引力常数值!
新智元报道 来源:Nature、科技日报编辑:闻菲、大明、肖琴 【导读】北京时间8月30日凌晨,Nature刊发了中科院院士罗俊团队历经30年最新测定的万有引力常数G值的结果,是迄今国际上最高精度的G值。实验使用了两种单独的G值测量方法,相关装置和细节均由团队自主研制完成,Nature刊文评论称,这项实验可谓“精确测量领域卓越工艺的典范”。万有引力常数G是最难测量的常数之一,确定
【算法】求平方根 - 二分法/牛顿迭代
题目 求一个数的平方根,要求返回小于等于平方根的正整数。 原理 二分法 遍历每次取中间数,大了就往小取,小了就往大取,直到取到正确的值。 牛顿迭代 求num的平方根,则是求 num / x 和 x 的均值,这个值会越来越趋近于真正的平方根。 比如求12的平方根,2 * 6 = 12,那么 (2 + 6) / 2的值就会更趋近于平方根。 代码 二分法 public stat
牛顿学院分享|软件测试过程中常用 Git 命令清单
Git是由LinusTorvalds创建的分布式版本控制器,它可以有效的管理和跟踪不同分支的变化,可以比较每个提交中代码的变化。一般来说,日常使用只要记住下图 6 个命令,就可以了。但是熟练使用,恐怕要记住 60~100 个命令。 下面是整理的常用 Git 命令清单。 Workspace:工作区 Index / Stage:暂存区 Repository:仓库区(或本地仓库) Remot
牛顿学院软件测试基础练习
软件测试基础练习第一部分 选择题: 1.下列哪一项不是白盒测试?( C ) A.单元测试 B.集成测试 C.系统测试 D.回归测试 2.属于黑盒测试的方法?( C ) A.基于基本路径 B.控制流 C.基于用户需求测试 D.逻辑覆盖 3.在 Assert类中断言对象为NUL是。( C ) A. assertEquals B. assertTrue C. assert\ull D. fail
力扣面试150 x 的平方根 二分 换底法 牛顿迭代法 一题多解
Problem: 69. x 的平方根 思路 👨🏫 参考题解 💖 袖珍计算器算法 class Solution {public int mySqrt(int x){if (x == 0)return 0;// Math.exp(3):e的三次方int ans = (int) Math.exp(0.5 * Math.log(x));return (long) (a
智能优化算法 | Matlab实现牛顿-拉夫逊优化算法Newton-Raphson-based optimize(内含完整源码)
文章目录 效果一览文章概述源码设计参考资料 效果一览 文章概述 智能优化算法 | Matlab实现牛顿-拉夫逊优化算法Newton-Raphson-based optimize(内含完整源码) 源码设计 % --------------------------------------------------------------------------
高等数学——手撕牛顿莱布尼茨公式
本文始发于个人公众号:TechFlow,原创不易,求个关注 今天是高等数学专题的第13篇文章,我们来看看定积分究竟应该怎么计算。 定积分的实际意义 通过之前的文章,我们基本上熟悉了定积分这个概念和它的一些简单性质,今天终于到了正题,我们要试着来算一算这个积分了。 我们先来回忆一下对定积分的直观感受,它可以代表一段曲形面积,比如: 如果我们把上图当中的f(x)看成是速度函数