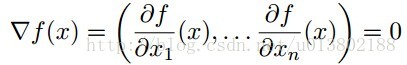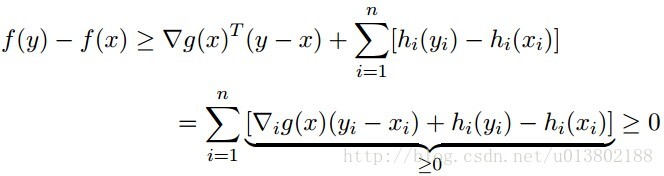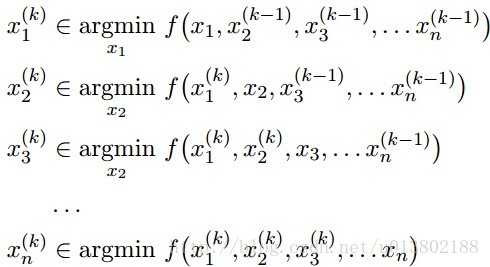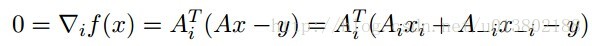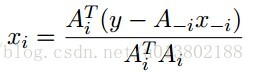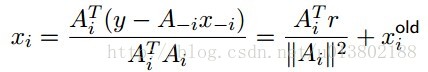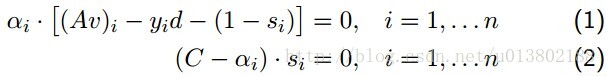本文主要是介绍超分辨率重建——梯度下降、坐标下降、牛顿迭代,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在阅读相关文献的时候,经常会遇到梯度下降,坐标下降,牛顿迭代这样的术语,今天把他们的概念整理一下。
梯度下降
整理自百度
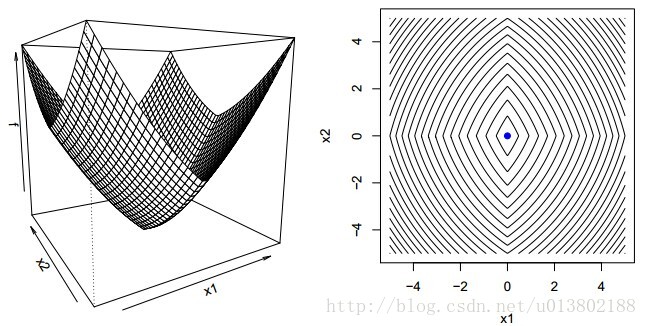
梯度下降法是一个最优化算法,通常也称为最速下降法。
%% 最速下降法图示
% 设置步长为0.1,f_change为改变前后的y值变化,仅设置了一个退出条件。
syms x;f=x^2;
step=0.1;x=2;k=0; %设置步长,初始值,迭代记录数
f_change=x^2; %初始化差值
f_current=x^2; %计算当前函数值
ezplot(@(x,f)f-x.^2) %画出函数图像
axis([-2,2,-0.2,3]) %固定坐标轴
hold on
while f_change>0.000000001 %设置条件,两次计算的值之差小于某个数,跳出循环x=x-step*2*x; %-2*x为梯度反方向,step为步长,!最速下降法!f_change = f_current - x^2; %计算两次函数值之差f_current = x^2 ; %重新计算当前的函数值plot(x,f_current,'ro','markersize',7) %标记当前的位置drawnow;pause(0.2);k=k+1;
end
hold off
fprintf('在迭代%d次后找到函数最小值为%e,对应的x值为%e\n',k,x^2,x)- 靠近极小值时收敛速度减慢。
- 直线搜索时可能会产生一些问题。
- 可能会“之字形”地下降。容易陷入局部最优解
问题的描述:给定一个可微的凸函数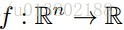
形式化的描述为:是不是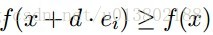
这里的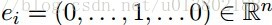
答案为成立。
这是因为:
但是问题来了,如果对于凸函数f,若不可微该会怎样呢?
答案为不成立,上面的图片就给出了一个反例。
那么同样的问题,现在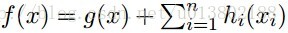
答案为成立。
证明如下,对每一个y
坐标下降(Coordinate descent):
这就意味着,对所有的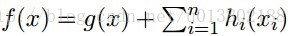
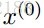
每一次我们解决了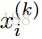
Tseng (2001)的开创性工作证明:对这种f(f在紧集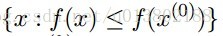

在实分析领域:
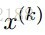
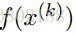
其中:
坐标下降的顺序是任意的,可以是从1到n的任意排列。
可以在任何地方将单个的坐标替代成坐标块
关键在于一次一个地更新,所有的一起更新有可能会导致不收敛
我们现在讨论一下坐标下降的应用:
线性回归:
令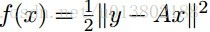
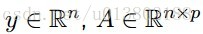
最小化xi,对所有的xj,j不等于i:
解得:
坐标下降重复这个更新对所有的
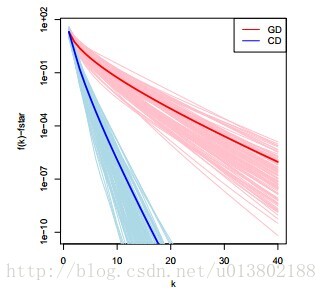
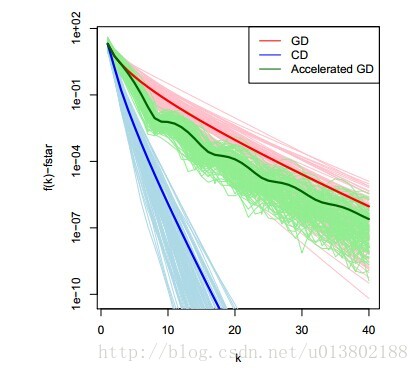
对比坐标下降与梯度下降在线性回归中的表现(100个实例,n=100,p=20)
将坐标下降的一圈与梯度下降的一次迭代对比是不是公平呢?是的。
其中r=y-Ax。每一次的坐标更新需要O(n)个操作,其中O(n)去更新r,O(n)去计算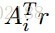
我们用相同的例子,用梯度下降进行比较,似乎是与计算梯度下降的最优性相违背。
那么坐标下降是一个一阶的方法吗?事实上不是,它使用了比一阶更多的信息。
现在我们再关注一下支持向量机:
SVM对偶中的坐标下降策略:
SMO(Sequentialminimal optimization)算法是两块的坐标下降,使用贪心法选择下一块,而不是用循环。
回调互补松弛条件(complementaryslackness conditions):
v,d,s是原始的系数,截距和松弛,其中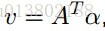
SMO重复下面两步:
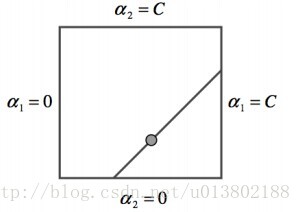
选出不满足互补松弛的αi,αj
第一步使用启发式的方法贪心得寻找αi,αj,第二步使用等式约束。
牛顿迭代法(Newton’s method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。
把f(x)在x0点附近展开成泰勒级数 f(x) = f(x0)+(x-x0)f’(x0)+(x-x0)^2*f”(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f’(x0)(x-x0)=0 设f’(x0)≠0则其解为x1=x0-f(x0)/f’(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f’(x(n))。
这篇关于超分辨率重建——梯度下降、坐标下降、牛顿迭代的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!