历时30年探索牛顿之谜，中国科学家测出迄今最高精度万有引力常数值！

  新智元报道 

来源：Nature、科技日报
编辑：闻菲、大明、肖琴

【导读】北京时间8月30日凌晨，Nature刊发了中科院院士罗俊团队历经30年最新测定的万有引力常数G值的结果，是迄今国际上最高精度的G值。实验使用了两种单独的G值测量方法，相关装置和细节均由团队自主研制完成，Nature刊文评论称，这项实验可谓“精确测量领域卓越工艺的典范”。万有引力常数G是最难测量的常数之一，确定G值对于检验万有引力和深入研究引力相互作用有重大意义，团队开发的技术和设备也已用于空间探索及引力波探测相关研究。

北京时间今天凌晨，Nature刊发了中科院院士罗俊团队最新测量的万有引力常数G值结果，这也是目前国际精度最高的G值，对于计量学和检测万有引力定律及一系列相关的空间引力探索都具有十分重大的意义。

万有引力常数是一个实验物理常数，用于计算两个物体间的引力大小。 通常出现在牛顿万有引力方程和爱因斯坦广义相对论中。 一般用大写G表示。

为了确保结果的精确性，罗俊院士团队这次使用了两种独立的传统引力测量方法，分别是扭秤周期法（TOS）和扭秤角加速度反馈法（AAF），并得到了两个结果：6.674184×10^-11和6.674484×10^-11立方米/千克/秒，相对精度大约为11.6ppm。（之前使用AAF方法获得的G的不确定性最低记录为13.7ppm。）

从上世纪80年代就已开始，罗俊院士团队就采用扭秤技术精确测量万有引力常数G，历经10多年的努力，在1999年得到了第一个G值，被随后历届的国际科学技术数据委员会（CODATA）录用。

2009年，团队又发表了新的测量结果，相对精度达到26ppm，是当时采用扭秤周期法得到的最高精度的G值，也被随后的历届CODATA所收录命名为HUST-09。

如今，罗俊团队再次一鸣惊人，给出了目前国际上最高精度的G值，相对不确定度优于12ppm，实现了对国际顶尖水平的赶超。

历经30年，测量迄今国际上精度最高的万有引力常数G值！

• 黎卿   华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 薛超   中山大学天琴引力物理研究中心，中山大学物理与天文学院

• 刘建平    华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 邬俊飞  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 杨山清  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 邵成刚  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 全立地  湖州大学工程学院

• 谭文海  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 涂良成  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 刘 祺  中山大学天琴引力物理研究中心，中山大学物理与天文学院

• Hao Xu  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 刘林霞  河南科技学院教学研究评估中心

• 王晴岚   湖北汽车工业大学理学院

• 胡忠坤  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 周泽兵  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 罗鹏顺  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• 吴书朝  华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室

• Vadim Milyukov   莫斯科国立大学斯科斯特恩伯格天文研究所

• 罗俊 华中科技大学物理学院, 基本物理量测量教育部重点实验室, 引力与量子物理湖北省重点实验室，中山大学天琴引力物理研究中心，中山大学物理与天文学院

使用两种测量万有引力常数装置，技术及细节全部自主研制

Nature同时刊发了Stephan Schlamminger的评论文章，Schlamminger在美国马里兰州盖瑟斯堡的国家标准与技术研究所基础电气测量小组工作。文章指出，控制重力相互作用强度的引力常数G很难准确测量。这也说明了罗俊院士团队以记录精度测量重力是一项了不起的成就。

1687年，牛顿发现了万有引力定律：两个质点彼此之间相互吸引的作用力，是与它们的质量乘积成正比，并与它们之间的距离成平方反比。用公式表示如下：

F=G（m₁m₂）/r²，其中G是万有引力常数

万有引力是四种基本力中最弱的一种。在太空星球间测量，比如地球和月球，这个力可能相当大。但如果是在实验室里，万有引力可能太小而无法准确测量。例如，两个相隔1米的1千克物体之间的引力仅相当于一些生物细胞的重量。由于这个原因，对这一引力的强度进行量化的引力常数G是最难以确定的物理常数之一。

1798年，科学家亨利·卡文迪什（Henry Cavendish）首次在实验室中使用一种称为扭秤的装置来确定引力常数G。在卡文迪什的实验中，它由一个哑铃组成，由细纤维悬挂在其中心。重力作用于哑铃末端，方向垂直于哑铃的杆和纤维的轴线。这种力导致哑铃围绕该轴旋转，导致纤维发生扭曲。

卡文迪什实验中使用的扭秤

最终，纤维的扭转力平衡了重力。记录哑铃在该位置的旋转角度。然后沿相反方向施加重力并测量第二旋转角度。从这两个角度之间的差计算出G的大小。

在扭转平衡实验中，重力由精确质量的外部组件提供。这些质量组件在两个或更多个不同位置之间移动，以改变力的方向和大小。因为哑铃在水平面上旋转，所以地球引力对实验的影响可以忽略不计。

多年来，科学家们已经开发了许多技术，利用扭转平衡来测量引力常数G。在这次实验中，罗俊院士团队构建了两个基于不同测量技术的薄板扭转平衡秤：分别基于摆动时间方法（TOS，下图左）和角加速度反馈方法（AAF）。

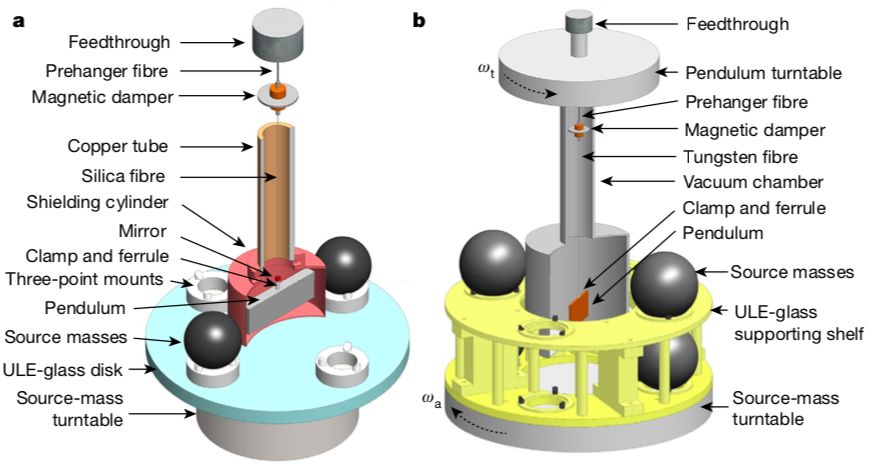
在TOS方法中，板的旋转是振荡的。当外部质量配置不同时，由振荡速度的变化计算出G。而在AAF方法中，使用两个转盘分别旋转扭转平衡秤和外部质量。当光纤的扭曲减小到零时，G由与扭转平衡秤相连的转盘的角加速度来确定。

新智元尝试着将论文的图说翻译如下：

在TOS方法中，摆锤是Al涂层的熔融石英块，尺寸为91×11×31立方毫米，质量约为68g。摆锤由薄的熔融石英纤维悬挂，直径为40-60μm，长度为900mm。磁阻尼器通过50毫米长、80微米直径的钨纤维悬挂。使用两个平均直径为57.2mm且真空、质量为778g的SS316不锈钢球作为源质量。

转盘用于改变球体在“近”和“远”方位间的位置（上图显示为“近”；在“远”的摆放位置中，转盘旋转90°）。安装在摆锤和球体之间的空心镀金铝圆柱体，用于保护系统免受静电场的影响。摆锤和源质量块放置在同一真空室内，通过离子泵维持约10的负5次方Pa的压力，摆锤扭转由光学杠杆监控。 

在AAF方法中，摆锤是镀金的熔融石英块，尺寸为91×4×50立方毫米，真空质量为40g。主光纤由钨纤维制成，长870毫米，直径25微米。磁阻尼器的设计与TOS方法相同。四个平均直径为127.0毫米、真空质量为8541克的SS316不锈钢球，用作位于具有上层和下层的ULE材料架上的源质量块。摆锤的小偏转角由自动准直仪记录。带有摆锤的腔室悬挂在一个空气轴承转盘下面，转盘与下方放置源质量块的转盘同轴安装。这套设备位于山洞实验室的被动保温室（passive thermal room）中。

根据《科技日报》报道，论文的通讯作者之一、团队核心成员、华中科技大学引力中心杨山清教授感慨：“从上世纪80年代罗俊院士开始进行万有引力常数G的精确测量实验研究至今，他已将其看作是毕生的事业，几十年如一日地在华中科技大学山洞实验室工作。罗院士不仅给我们提供了方向的指引，同时以身作则，对实验过程中的每个重要阶段他都主动带领团队成员一起分析、讨论并指导大家做实验。一批兼具理论与实践能力的优秀人才在此过程中得以成长。”

论文地址：

https://www.nature.com/articles/s41586-018-0431-5