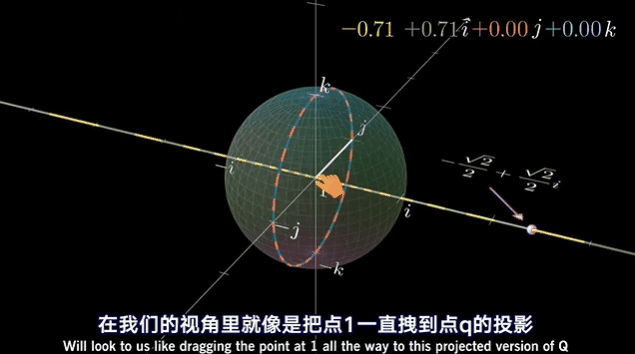
四元专题
Unity中使用四元数限制旋转
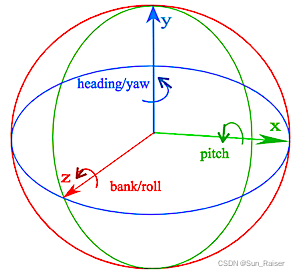
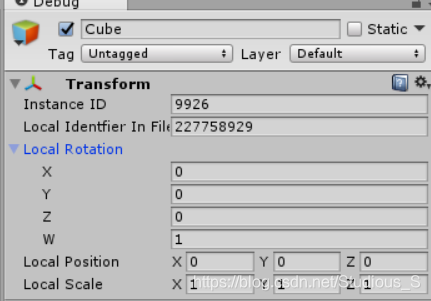
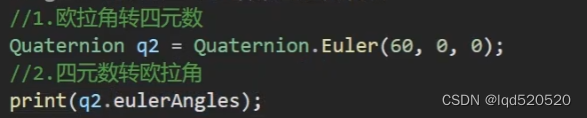
前言 在处理旋转相关的内容的时候,如果使用unity提供的欧拉角描述旋转,会出现一下两种问题 同一旋转的表示不唯一万向节死锁 绕轴90°旋转与绕轴90°+360°旋转的表现是一致的 当某个特定轴达到某个特殊值时,绕一个轴旋转可能会覆盖另一个轴的旋转从而失去一维自由度Unity中x轴达到90度时,会产生万向节死锁。x轴为90度,此时调节y或z轴
【自动驾驶】26.【很清晰】旋转矩阵,欧拉角,四元数,旋转向量和齐次变换矩阵
原文链接:https://blog.csdn.net/varyshare/article/details/91899049 前言 这几个名词都是用来描述一个物体的位置和姿态的。它们之间可以相互转化,而且各有各的优点与缺点。我先把这几个名词之间的联系理清楚,然后再解释他们各自适合的领域以及为何需要他们。 1.旋转矩阵 旋转矩阵的初衷就是人们希望给定一个向量x,然后我对它旋转,能直接通过矩阵乘法的
【自动驾驶】24.欧拉角、旋转向量、四元数、万向锁
原文链接:https://blog.csdn.net/shenxiaolu1984/article/details/50639298 原文链接:https://blog.csdn.net/lql0716/article/details/72597719 三维空间刚体旋转有两种方式: (1) 任何一个旋转可以表示为依次绕着三个旋转轴旋三个角度的组合。这三个角度称为欧拉角。(2) 三维空间的任意旋
【强烈推荐】四元数与三维旋转
目录 1 强烈推荐讲解四元数与三维旋转的这篇文章,深入浅出2 笔记2.1 复数2.1.1 复数的定义2.1.2 复数的乘法与二维旋转 2.2 三维空间中的旋转2.2.1 角轴2.2.2 旋转的分解 2.3 四元数2.3.1 四元数的定义2.3.2 四元数的乘法2.3.3 四元数与三维旋转2.3.4 三维旋转的矩阵形式 1 强烈推荐讲解四元数与三维旋转的这篇文章,深入浅出
计算机视觉与深度学习 | Matlab实现旋转矩阵R到四元数的转换(源代码)
================================================ 博主github:https://github.com/MichaelBeechan 博主CSDN:https://blog.csdn.net/u011344545 ================================================ 代码理论参考:《视觉SLAM十四讲
刚体运动描述:欧拉角与四元数
在机器人学中,刚体的运动描述是非常重要的,特别是当我们需要精确控制机器人的姿态时。欧拉角和四元数是两种常用的描述刚体在三维空间中旋转的方法。下面将分别介绍这两种方法并给出其特点。 欧拉角 定义与特点: 定义:欧拉角是通过绕一个三维坐标系的三个轴依次旋转来定义的,通常按照某个固定的旋转顺序(如XYZ、ZYX等)进行。表示:欧拉角由三个角度组成,分别对应绕三个坐标轴的旋转。例如,在RPY(Rol
一个可复用的C++ 3阶实方阵类和4阶实方阵类(兼容与扩展了DX中的4阶实方阵类);四元数(quaternion)模板类的使用
一个可复用的C++ 3阶实方阵类和4阶实方阵类(兼容与扩展了DX中的4阶实方阵类) 部分DX矩阵函数的实现 namespace Han { FLOAT WINAPI D3DXMatrixDeterminant(CONST D3DXMATRIX *pM) { D3DXMATRIX mtx=*pM; FLOAT ret=Bsdet(&mtx(
【p1】求表达式的四元式
前言 这是自己复习编译原理的一个系列 的文章,首先是网课部分,有15集,每一集我都会做一个详细的笔记,看了一遍网课,但是感觉还是难以融会贯通,做做笔记,加深理解 自己之后再复习,也是先看一下网课,主要是要理解,好像需要记忆的只有少数几个公式 写出表达式的四元式 四元式的格式是 (运算符,运算对象,运算对象,临时变量) 意思是把计算的结果存在一个临时变量里面,这个临时变量继续参加后续的计算
四元数导数,四元数变化率运动学方程
四元数乘法 这里首先需要介绍四元数乘法,假设有两个四元数 q a , q b q_a, q_b qa,qb,如下所示: q a = q a 0 + q a 1 i + q a 2 j + q a 3 k = [ s a , v a ] T q b = q b 0 + q b 1 i + q b 2 j + q b 3 k = [ s b , v b ] T \begin{aligned}
【无人机/平衡车/机器人】详解STM32+MPU6050姿态解算—卡尔曼滤波+四元数法+互补滤波(文末附3个算法源码)
效果: MPU6050姿态解算-卡尔曼滤波+四元数+互补滤波 目录 基础知识详解 欧拉角
中间代码生成-四元式
代码: import tkinter as tkroot = tk.Tk()root.geometry("800x600+50+50")root.title("中间代码生成")label2 = tk.Label(root, text = "请输入赋值语句:")label2.place(x=10,y=10)label3 = tk.Label(root, text = "四元式序列:")la
Unity中的四元数和旋转
文章目录 四元数Unity中使用四元数表示旋转案例描述代码 注 四元数 四元数用来表示一个物体的位置,或者旋转。这两种其实是等价的。我们可以说一个三维向量 ( x , y , z ) (x,y,z) (x,y,z)可以表示一个物体的空间位置,也可以表示位移。因为任何一个三维向量可以表示原物体相对于位置 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)的位移。同样,
四元数和旋转轴及旋转角度之间的转换理解实例
主观心得: 四元数与旋转轴是一一对应的关系。除了相差一个标量倍数外( 标量倍数,是指这么一个意思:对于任何数或者向量a,a与k*a(k是一个实数)本质上是相等的。如a= [1 2 3],b= [2 4 6]或者b=[0.1 0.2 0.3])都是相等的。 四元数的定义:q = [w,x,y,z]其中w是实部,当然也有资料会把四元数写成q = [x,y,z,w]其中w是实
Quaternion四元数与旋转
http://hi.baidu.com/xiongvb/blog/item/eec1b90293e5fd174bfb51f0.html http://cl314413.blog.163.com/blog/static/190507976201241914452590/
MSCKF2讲:JPL四元数与Hamilton四元数
MSCKF2讲:JPL四元数与Hamilton四元数 文章目录 MSCKF2讲:JPL四元数与Hamilton四元数2 JPL四元数2.1 定义与区别2.2 JPL四元数的乘法2.3 反对称矩阵2.4 Ω ( ω ) \Omega(\omega) Ω(ω)矩阵2.5 JPL四元数与旋转矩阵的转换2.6 JPL四元数导数2.7 JPL四元数积分2.7.1 0阶积分2.7.2 1阶积分 3
3D 中的方位与角位移(旋转矩阵、欧拉角、四元数)
文章目录 一、3D 中的方位与角位移1. 欧拉角 (Euler angles)2. 四元数的相关知识2.1 复数2.2 欧拉旋转定理2.3 三维空间旋转的拆分 3. 四元数 (Quaternion)3.1 四元数的运算3.2 四元数默认在极坐标下3.3 四元数的常用插值方法3.4 贝塞尔曲线和 Squad 插值 4 欧拉角、旋转矩阵、四元数的互相转换4.1 欧拉角和旋转矩阵4.2 四元数和旋
从零开始学习PX4源码1(两个三维矢量如何转换成四元数)
目录 文章目录 目录摘要参考网址推导过程 摘要 本节主要记录px4如何从两个三维旋转矢量转换到四元数的过程,欢迎批评指正!!! 参考网址 三维矢量转四元数 推导过程
四元数如何进行标准化?
假设有一个四元数的张量 r,它包含了两个四元数: r = [ 1 2 3 4 4 3 2 1 ] r = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \\ \end{bmatrix} r=[14233241] 这里,第一个四元数是 q 1 = ( 1 , 2 , 3 , 4 ) q_1 = (1, 2, 3, 4) q1=(1,2,
Unity3D-----欧拉角与四元数
欧拉角与四元数 一、欧拉角1、什么是欧拉角2、欧拉角的优点3、欧拉角的缺点3.1 万向节死锁 二、四元数1、什么是四元数2、基本运算2.1 与向量相乘2.2 与四元数相乘 3、优点4、缺点 一、欧拉角 1、什么是欧拉角 欧拉角是使用三个角度来保存方位。X与Z沿自身坐标系旋转,Y沿世界坐标系旋转API :Vector3 eulerAngle = this.transform.
四元数与角轴、旋转矩阵、so(3)、SO(3) 的关系
四元数定义 q = [ s , υ ] T , s = q 0 ∈ R , υ = [ q 1 , q 2 , q 3 ] T ∈ R 3 \left.q=\left[\begin{matrix}{s,\upsilon}\\\end{matrix}\right.\right]^{\mathrm{T}},s=q_{0}\in\mathbb{R},\upsilon=\left[\begin{mat
Unity之四元数计算
四元数相乘 #region 四元数相乘Quaternion q = Quaternion.AngleAxis(20, Vector3.up);this.transform.rotation *= q;#endregion 四元数乘向量 Vector3 v = Vector3.forward;print(v);//四元数乘向量的顺序不能改变,也就是说不能用向量去乘四元数,只能是四元数
Unity中四元数常用的方法
单位四元数 #region 单位四元数print(Quaternion.identity);testObj.rotation = Quaternion.identity;//初始化对象时可能会用来赋值Instantiate(testObj,Vector3.zero,Quaternion.identity);#endregion 插值运算 #region 插值运算//四元数中也提供了如同V