Unity3D-----欧拉角与四元数

本文主要是介绍Unity3D-----欧拉角与四元数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、欧拉角

1、什么是欧拉角

• 欧拉角是使用三个角度来保存方位。
• X与Z沿自身坐标系旋转，Y沿世界坐标系旋转
• API ：Vector3 eulerAngle = this.transform.eulerAngles;
  在Unity中欧拉角就是transofrm.rotation，如图所示
  

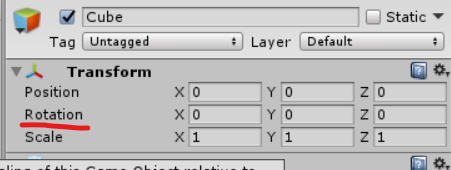
2、欧拉角的优点

• 仅使用三个数字表达方位,占用空间小。
• 沿坐标轴旋转的单位为角度，符合人的思考方式。
• 任意三个数字都是合法的，不存在不合法的欧拉角

3、欧拉角的缺点

• 对于同一个方位，存在多个欧拉角描述，因此无法判断多个欧拉角代表的角位移是否相同。
• 例如
  – 角度（0，5，0）与（0，365，0）
  – 角度（0，-5，0）与（0，355，0）
• 为了保证任意方位都只有独一无二的表示，Unity引擎限制了角度范围，即沿X轴旋转限制在-90°(270°)到90°之间，沿Y与Z轴旋转限制在0°到360°之间。
  提示：在unity5.x版本当中，在面板直接修改x，y，z的值并不会受到限制，但是当用代码进行修改时，就可观察到x，y，z的值是受到限制的，以确保任意方位都只有独一无二的表示。
  可用一下代码进行测试 :

 public class EuleDem : MonoBehaviour 
{public void OnGUI(){if (GUILayout.RepeatButton("沿x轴旋转")){this.transform.eulerAngles += new Vector3(1, 0, 0);}if (GUILayout.RepeatButton("沿y轴旋转")){Vector3 euler = this.transform.eulerAngles;this.transform.eulerAngles += new Vector3(0, 1, 0);}if (GUILayout.RepeatButton("沿z轴旋转")){Vector3 euler = this.transform.eulerAngles;this.transform.eulerAngles += new Vector3(0, 0, 1);}}
}

3.1 万向节死锁

• 物体沿X轴旋转±90度，自身坐标系Z轴与世界坐标系Y轴将重合，此时再沿Y或Z轴旋转时，将失去一个自由度。
• 在万向节死锁情况下，规定沿Z轴完成绕竖直轴的全部旋转，即此时Y轴旋转为0
• 可用上面的代码进行测试，先将X旋转至±90，然后再持续点击沿Y轴旋转或沿Z轴旋转的按钮，会发现Y轴的角度是始终为0的，那么这就无法使物体能够进行空间上的360°旋转。
  四元数可避免万向节死锁

二、四元数

1、什么是四元数

• Quaternion 在3D图形学中代表旋转，由一个三维向量（X/Y/Z）和一个标量（W）组成
• 旋转轴为V，旋转弧度为h,如果使用四元数表示，则四个分量为:
  x=sin(h/2)*V.x----------y=sin(h/2)*V.y
  z=sin(h/2)*V.z----------w=cos(h/2)
• X,Y,Z,W的取值范围是-1到1.
• API ： Quaternion qt=this.transform.rotation
  将模式调整为debug模式，可看到四元数
  

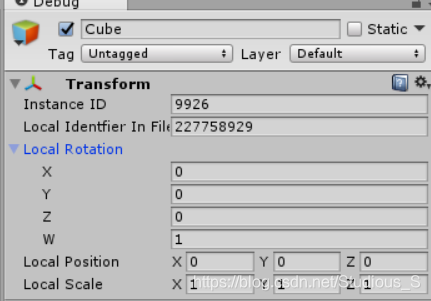
2、基本运算

2.1 与向量相乘

• 四元数左乘向量，表示将该向量按照四元数表示的角度旋转。
• 例如
  Vector3 point=new Vecotor3（0，0，10）
  Vector3 newPoint = Quaternion.Euler（0,30,0） * point

2.2 与四元数相乘

• 两个四元数相乘可以组合旋转效果
• 例如

Quaternion rotation01=Quaternion.Euler(0,30,0) * Quaternion.Euler(0,20,0);
Quaternion rotation02=Quaternion.Euler(0,50,0)
rotation01与rotation02效果是一样的

3、优点

• 可避免万向节死锁

4、缺点

• 难于使用，不建议单独修改某个数值，可能会出现异常
• 存在不合法的四元数

这篇关于Unity3D-----欧拉角与四元数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---