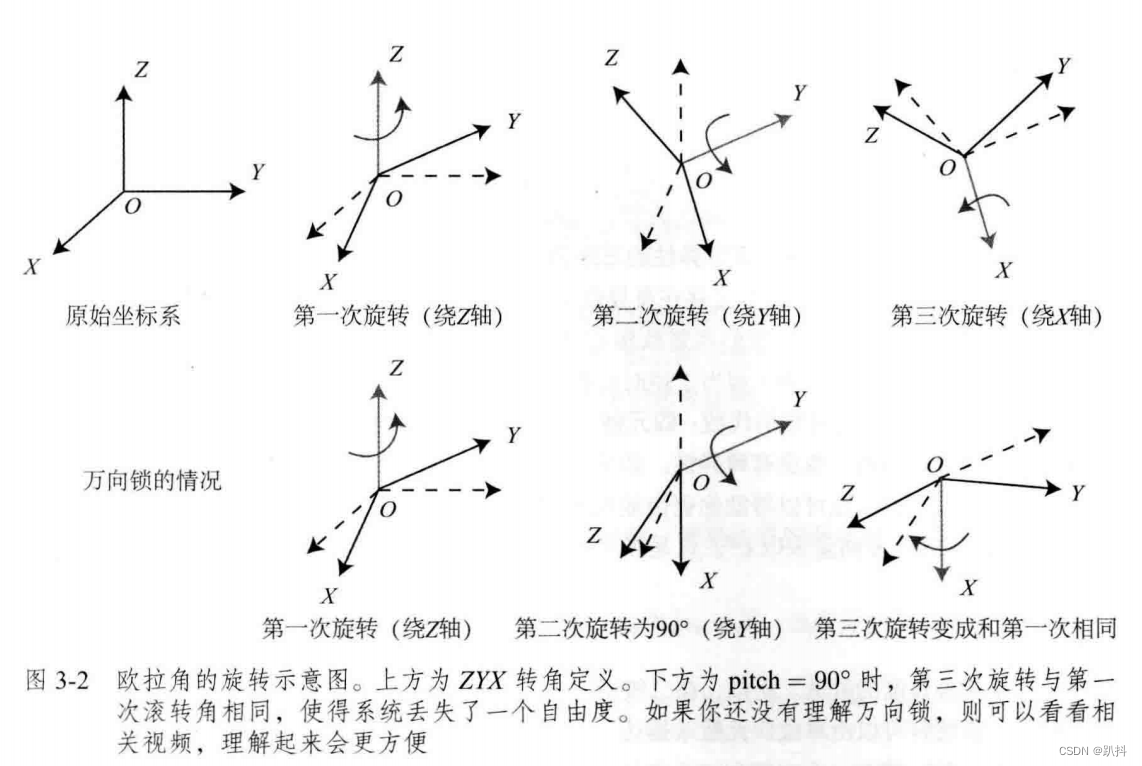
欧拉角专题
【自动驾驶】26.【很清晰】旋转矩阵,欧拉角,四元数,旋转向量和齐次变换矩阵
原文链接:https://blog.csdn.net/varyshare/article/details/91899049 前言 这几个名词都是用来描述一个物体的位置和姿态的。它们之间可以相互转化,而且各有各的优点与缺点。我先把这几个名词之间的联系理清楚,然后再解释他们各自适合的领域以及为何需要他们。 1.旋转矩阵 旋转矩阵的初衷就是人们希望给定一个向量x,然后我对它旋转,能直接通过矩阵乘法的
【自动驾驶】24.欧拉角、旋转向量、四元数、万向锁
原文链接:https://blog.csdn.net/shenxiaolu1984/article/details/50639298 原文链接:https://blog.csdn.net/lql0716/article/details/72597719 三维空间刚体旋转有两种方式: (1) 任何一个旋转可以表示为依次绕着三个旋转轴旋三个角度的组合。这三个角度称为欧拉角。(2) 三维空间的任意旋
ROS中四元素和欧拉角转换
Yaw角到Quaternion geometry_msgs::Quaternion geo_q = tf::createQuaternionMsgFromYaw(refLinePose_.yaw); Quaternion到Yaw角 double yaw=tf::getYaw(i.pose.orientation); //
刚体运动描述:欧拉角与四元数
在机器人学中,刚体的运动描述是非常重要的,特别是当我们需要精确控制机器人的姿态时。欧拉角和四元数是两种常用的描述刚体在三维空间中旋转的方法。下面将分别介绍这两种方法并给出其特点。 欧拉角 定义与特点: 定义:欧拉角是通过绕一个三维坐标系的三个轴依次旋转来定义的,通常按照某个固定的旋转顺序(如XYZ、ZYX等)进行。表示:欧拉角由三个角度组成,分别对应绕三个坐标轴的旋转。例如,在RPY(Rol
利用ESP32(Arduino IDE)向匿名上位机发送欧拉角
文章目录 一. 匿名上位机介绍二. 匿名协议说明1. 匿名协议官方说明文档2. 协议说明 三. 向匿名上位机发送数据(基于Arduino IDE的esp32)四. 运行效果 一. 匿名上位机介绍 匿名上位机官方介绍视频 匿名上位机官方下载 二. 匿名协议说明 1. 匿名协议官方说明文档 官方对于协议的说明文档可以在下载的匿名上位机中打开,是一份PDF文档 2.
UR机械臂位置数据旋转矢量与欧拉角变换
UR机械臂位置数据旋转矢量与欧拉角变换 本文介绍在UR机械臂控制过程在,使用函数返回的数据为旋转矢量,但是该数据对于控制非常不友好,我们需要将旋转转化为欧拉角的数据,才可以直观观察到工具端相对于不同轴旋转的角度。本文针对这一问题,描述旋转矢量与欧拉角转换的概念,以及如何通过Python代码进行两者之间相互转换的函数。 参考链接:https://forum.universal-robo
齐次变换矩阵、欧拉角
齐次变换矩阵 因为老是忘记齐次变换矩阵的含义以及方向,每次推导公式都很费劲,写下这篇文章用于快速回顾齐次变换矩阵。 表示的是:坐标系A到坐标系B的齐次变换矩阵,也是坐标系B在坐标系A下的位姿。 对于这个矩阵,有三个物理意义: (1)坐标变换:通过变换矩阵可以获得{B}坐标系下的向量(坐标)在{A}坐标系下的描述(坐标)。(2)坐标系的描述:描述了坐标系{B}在{A}下的位姿(位置和姿态
使用python进行欧拉角和旋转矩阵变换
一. 配置PIP镜像源 pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple 二.下载numpy等库 pip install scipy 三.欧拉角转旋转矩阵(右手坐标系, ZXY顺序) # coding=UTF-8from scipy.spatial.transform
矩阵Matrix到欧拉角Euler转换
参考文献: http://www.geometrictools.com/Documentation/EulerAngles.pdf 但是这里的公式不能直接用,原因是左右手系空间不同,我这边采用Direct3D默认的右手系,参考: https://docs.microsoft.com/en-us/windows/win32/direct3d9/d3dxmatrixrotationyawpitc
unity欧拉角之图文并茂通俗理解
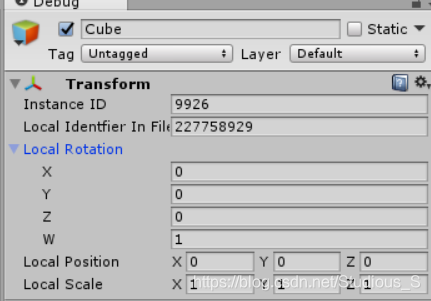
unity的欧拉角总是基于当前坐标系的x,y,z轴旋转的,假如一个物体x,y,z三轴都有旋转角度,那么旋转的顺序是,y轴-》x轴-》z轴。 也就是说先在本地坐标沿着y轴旋转y角度,得到一个新的x,y,z坐标系,再沿着此坐标系的x轴旋转x角度,再得到一个新的坐标系,再沿着此坐标系的z轴旋转z角度。此时如果把x,y,z理解成父,子关系,让人很难想象和理解,因为缺少了顺序这个特性。 下面出图说明(红
python脚本实现全景站点矩阵转欧拉角
效果 脚本 import reimport numpy as npimport mathimport csvfrom settings import *# 以下是一个示例代码,可以输入3*3旋转矩阵,然后输出旋转角度:# ,输入3*3旋转矩阵# 计算x,y,z旋转角def rotation_matrix_to_euler_angles(R):
3D 中的方位与角位移(旋转矩阵、欧拉角、四元数)
文章目录 一、3D 中的方位与角位移1. 欧拉角 (Euler angles)2. 四元数的相关知识2.1 复数2.2 欧拉旋转定理2.3 三维空间旋转的拆分 3. 四元数 (Quaternion)3.1 四元数的运算3.2 四元数默认在极坐标下3.3 四元数的常用插值方法3.4 贝塞尔曲线和 Squad 插值 4 欧拉角、旋转矩阵、四元数的互相转换4.1 欧拉角和旋转矩阵4.2 四元数和旋
Unity3D-----欧拉角与四元数
欧拉角与四元数 一、欧拉角1、什么是欧拉角2、欧拉角的优点3、欧拉角的缺点3.1 万向节死锁 二、四元数1、什么是四元数2、基本运算2.1 与向量相乘2.2 与四元数相乘 3、优点4、缺点 一、欧拉角 1、什么是欧拉角 欧拉角是使用三个角度来保存方位。X与Z沿自身坐标系旋转,Y沿世界坐标系旋转API :Vector3 eulerAngle = this.transform.
计算2个空间向量支架的夹角(固定系欧拉角XYZ)分量
前提:固定系欧拉角,旋转顺序XYZ 直接用py文件简单计算: from scipy.spatial.transform import Rotationimport numpy as npdef calculate_euler_angles(vec1, vec2, rotation_order='xyz'):# 将法向量转换为单位向量vec1_normalized = vec1 / np.
姿态解算知识点2——欧拉角微分方程求解角速度
1.目标 地理坐标系的角速度 2.已知量 机体坐标系的角速度 gyro_x, gyro_y,gyro_z;欧拉角,pitch,roll,yaw,参考我的上一章节姿态解算知识点1——四元数互补滤波 3.算法总框图 4.数学模型和公式推导 这里坐标系取东北天 --- 右前上 由以上求得地理坐标系的角速度为: 5.代码实现 欧拉角微分方程算法代码 6.
姿态解算知识点1——四元数互补滤波求解欧拉角
1.目标 求四元数q0、q1、q2、q3; 求解飞行器、机器人的欧拉角pitch、roll、yaw; 2.算法总框图 3.四元数数学模型及公式推导 上面的b系就是机体坐标系,R系可以认为是导航坐标系(即地理坐标系n)。 4. 四元数更新代码实现 /*******************************************
基于C#的机械臂欧拉角与旋转矩阵转换
欧拉角概述 机器人末端执行器姿态描述方法主要有四种:旋转矩阵法、欧拉角法、等效轴角法和四元数法。所以,欧拉角是描述机械臂末端姿态的重要方法之一。 关于欧拉角的历史,由来已久,莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于任何参考系,一个刚体的取向,是依照顺序,从这参考系,做三个欧拉角的旋转而设定的。所以,刚体的取向可以用三个基本旋转矩阵来决定。换句话说,任何关于刚体旋转的旋转矩
一文读懂旋转矩阵,欧拉角,以及万向锁问题
一文读懂旋转矩阵,欧拉角,以及万向锁问题 一:物体的姿态描述 物体的姿态可由固定于此物体的坐标系描述,为了规定空间某刚体B的姿态,设置一直角坐标系{B}与此刚体固接。用坐标系{B}的三个单位主矢量{Xb,Yb,Zb}相对于参考坐标系{A}的方向余弦组成的3*3的矩阵来表示刚体B相对于坐标系{A}的方位,(_B^A)R称为旋转矩阵。 式中,上标A代表参考坐标系{A},下表B代表被描述的坐标系{
用欧拉角表示旋转(方位)heading pitch bank 含义,形象的图示
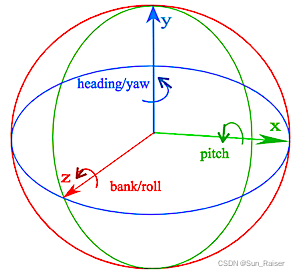
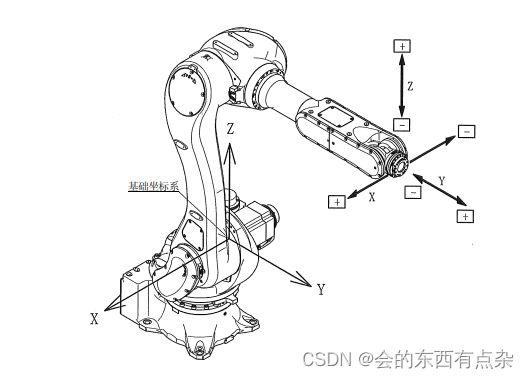
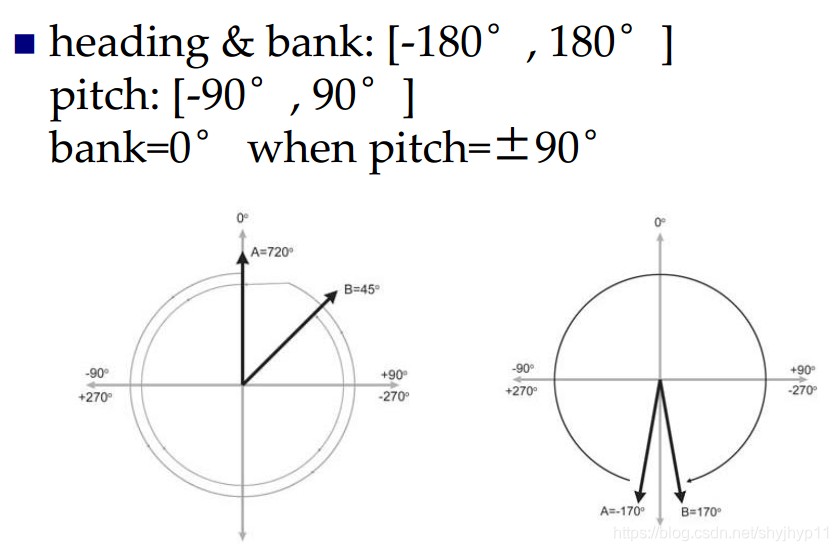
1. 简介 2. heading pitch bank 含义 heading: 物体绕自身的对象坐标系的Y轴,旋转的角度,下图中,对象坐标系与场景坐标系是重合的。 pitch: 物体绕自身的对象坐标系的X轴,旋转的角度,下图中,对象坐标系与场景坐标系未重合的。 bank: 物体绕自身的对象坐标系的Z轴,旋转的角度,下图中,对象坐标系与场景坐标系未重合的。 3.
四元数,欧拉角,旋转矩阵,旋转向量
四元数,旋转矩阵,旋转向量,欧拉角 一、欧拉角 1、欧拉角是表达旋转的最简单的一种方式,形式上它是一个三维向量,其值分别代表物体绕坐标系三个轴(x,y,z轴)的旋转角度,默认旋转正向为逆坐标轴逆时针方向。 2、在旋转过程中,xyz轴方向并不是固定不变的,而是随着前面的旋转而改变。比如如果绕 x 轴旋转 90 度,那么旋转后的 y 轴正向将指向原始的 z 轴方向,而旋转后的 z 轴正向将指向
[转]游戏动画中欧拉角与万向锁的理解
我在2009年5月份左右拜读了《3D数学基础:图形与游戏开发》,当时对欧拉角中万向锁的概念一直是百思不得其解,也从未遇到过这种情况。书上有这样一句话:“如果您从来没有遇到过万向锁情况,你可能会对此感到困惑,而且不幸的是,很难在本书中讲清楚这个问题,你需要亲身经历才能明白。”今天我用3个多小时的时间再次回想了一下这个问题,总算想明白了,现在把思考的结果分享给大家.
【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵 【视觉SLAM十四讲学习笔记】第三讲——Eigen库 本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动? 旋转向量 矩阵表示方式至少有一下两个缺点: SO(3)的旋转矩阵有9个量,但一次旋
Apollo学习笔记(25)旋转矩阵、欧拉角、四元数理论及其转换关系
1.概述 做MPC控制的时候,需要把 map 坐标系下的相关坐标点转换到 car 坐标系中,由于是只考虑 xy 平面,所以计算比较简单。做完之后,考虑到三维空间的坐标系转换还是不太懂,主要是ROS系统中的tf变换,于是摸了两天鱼。今天详细的记录下来,旋转矩阵、四元素、欧拉角以及各个之间的转换关系。 阅读了好几篇大神的文章,具体也找不到连接了,在此顶礼膜拜,如有相似的地方,那就相似吧,毕竟原理都一
数学概率 | 旋转矩阵、欧拉角、四元数
目录 一,旋转矩阵 二维旋转矩阵 三维旋转矩阵 二,欧拉角 三,四元数 四,矩阵、欧拉角、四元数相互转换 四元数转矩阵 矩阵转四元数 欧拉角转矩阵 矩阵转欧拉角 欧拉角转四元数 四元数转欧拉角 一,旋转矩阵 二维旋转矩阵 R() = 推导,以二维平面为例旋转: = cos( + ) = coscos - sinsin = cos *











![[转]游戏动画中欧拉角与万向锁的理解](/front/images/it_default.jpg)