【自动驾驶】24.欧拉角、旋转向量、四元数、万向锁

本文主要是介绍【自动驾驶】24.欧拉角、旋转向量、四元数、万向锁，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原文链接：https://blog.csdn.net/shenxiaolu1984/article/details/50639298
原文链接：https://blog.csdn.net/lql0716/article/details/72597719

三维空间刚体旋转有两种方式：

(1) 任何一个旋转可以表示为依次绕着三个旋转轴旋三个角度的组合。这三个角度称为欧拉角。
(2) 三维空间的任意旋转，都可以用绕三维空间的某个轴旋转过某个角度来表示。

绕坐标轴的多次旋转可以等效为绕某一轴旋转一定角度，我感觉这就是四元数最直观的几何意义了。不管是RPY还是欧拉角，都可以利用四元数来代替表达。可以参考下面这篇博文：
https://www.cnblogs.com/21207-iHome/p/6894128.html

`1.欧拉角的物理意义：`

任何一个旋转可以表示为依次绕着三个旋转轴旋三个角度的组合。这三个角度称为欧拉角。
三个轴可以指固定的世界坐标系轴，也可以指被旋转的物体坐标系的轴。三个旋转轴次序不同，会导致结果不同。
本文中提到的欧拉角指：绕着世界坐标系的x,y,z轴，依次旋转的结果。其取值范围如下：

在这里插入图片描述

欧拉角→旋转矩阵
单独绕一个轴旋转θ角度的旋转矩阵为：
在这里插入图片描述
如果依次绕x轴、y轴、z轴旋转，该变换的旋转矩阵为：

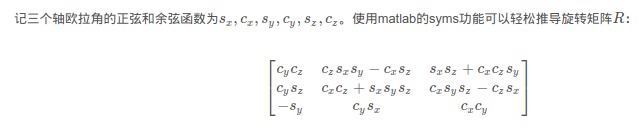
`2.四元数的物理意义：`

`旋转向量`

三维空间的任意旋转，都可以用绕三维空间的某个轴旋转过某个角度来表示，即所谓的Axis-Angle(轴角)表示方法。轴角，就是绕一个轴旋转某个角度，来表示一个旋转。

这种表示方法里，Axis(轴)可用一个三维向量(x,y,z)来表示，θ可以用一个角度值来表示。

直观来讲，一个四维向量(θ,x,y,z)就可以表示出三维空间任意的旋转。注意，这里的三维向量(x,y,z)只是用来表示axis(轴)的方向朝向，因此更紧凑的表示方式是用一个单位向量来表示方向axis(轴)，而用该三维向量的长度来表示角度值θ。

这样以来，可以用一个三维向量(θ∗x,θ∗y,θ∗z)就可以表示出三维空间任意的旋转，前提是其中(x,y,z)是单位向量，即 $\color{red}x^2 + y^2 + z^2 = 1$ 。这就是旋转向量(Rotation Vector)的表示方式，OpenCV里大量使用的就是这种表示方法来表示旋转(见OpenCV相机标定部分的rvec)。

`四元数`

前面的旋转向量中的单位向量(x,y,z)旋转θ角度后的四元数：
在这里插入图片描述
对于三维坐标的旋转，可以通过四元数乘法直接操作，与旋转矩阵操作可以等价，但是表示方式更加紧凑，计算量也可以小一些。

需要注意，单位向量(x,y,z)指的是这个向量长度为1，即 $\color{red}x^2 + y^2 + z^2 = 1$ ，这个向量是表示的这个轴的位置，表述某个向量时，一般会把这个向量用单位向量表示，下面的(w1,w2,w3)就是单位向量(x,y,z)，写法不一致而已。

四元数的模是四元数到原点的距离。如果某个四元数(q0, q1, q2, q3)的模长为1，即满足 $\sqrt {q_0^2 + q_1^2 + q_2^2 + q_3^2}=1$ 。但并不是说所有四元数的模都为1。只有表示旋转的四元数的模才为1,所以上面旋转向量的模才为1。不要混淆了。
在这里插入图片描述
注意，上面的w1,w2,w3不是i,j,k, 不要搞混了。[w1,w2,w3]是通过原点的某个轴上的单位长度(长度为1)的点，即 $w_1^2+ w_2^2 + w_3^2 =1$ 。
[w1,w2,w3]是个三维坐标点，设为点P，则OP就是这个旋转轴，w1,w2,w3分别为距离坐标系原点O的三个方向的距离。

欧拉角的缺点：

1、欧拉角的表示方式不唯一。给定某个起始朝向和目标朝向，即使给定yaw、pitch、roll的顺序，也可以通过不同的yaw/pitch/roll的角度组合来表示所需的旋转。这其实主要是由于万向锁(Gimbal Lock)引起的；
2、欧拉角的插值比较难；
3、计算旋转变换时，一般需要转换成旋转矩阵，这时候需要计算很多sin, cos，计算量较大；

对于三维坐标的旋转，可以通过四元数乘法直接操作，与旋转矩阵操作可以等价，但是表示方式更加紧凑，计算量也可以小一些。

`万向锁`

请参考原文：https://zhuanlan.zhihu.com/p/74040465

为了更好的理解这个现象，我们再用自己的手机做一个试验：

把手机屏幕朝上，手机的长边为X轴，短边为Y轴，Z轴垂直屏幕向下。
你先绕Z轴旋转一下手机，假设旋转30度；
然后再把手机绕Y轴旋转90度，也就是把手机短边接触桌面，长边竖立起来；
这时候你再绕手机的长边(X轴)旋转，你会发现手机的短边一直定在桌面上不可能脱离桌面，这就是万向锁现象。

下面这个说法，是从方向自由度来说明的：
需要注意的是XYZ轴的定义动态跟从手机的方向，例如Z轴永远是手机屏幕所示方向。
按Z->Y->X的顺序来旋转手机，不过规定Y旋转的角度为90°。
这样做的时候你会发现无论你怎样选择Z和X的旋转角度，手机的短边都无法离开桌面。这意味着什么呢？这意味着虽然你看似有X、Z旋转的2向自由度，但是当Y被定为90的时候，这个系统实际上只有一向自由度，因为任何两向自由度的旋转一定可以使任一直线离开任一平面，而我们绕Z轴和x轴随便转却并不能将手机的短边移开桌面。

下面这个说法，是从绕X、Z轴分别旋转不同角度却能达到同样效果来说明：
首先旋转顺序就是Z-Y-X，绕完Y轴旋转后，只能绕X轴旋转了，不能再绕Z轴旋转了；
举例：

转法1：你先绕Z正方向旋转30°，再绕Y正方向旋转90°，最后绕X轴旋转30°，见下图左；
转法2：你先绕Z正方向旋转20°，再绕Y正方向旋转90°，最后绕X轴旋转40°，见下图右；
实线是最开始没旋转的，虚线矩形是绕Z轴旋转后的，绕y轴旋转后的由于是竖直方向的，所以没画出来，箭头指向的那个虚线是绕X轴旋转的角度。下面两幅图最终都达到了同样的效果，角度都为60°。

你会发现两种转法的结果是一样的，所以说先绕Z旋转的度数和最后绕X的旋转度数，没啥区别了。最终的结果就是，你绕X轴旋转的角度，也可以通过旋转Z轴来达到同样；或者，你绕Z轴旋转的角度，也可以通过旋转X轴来达到同样效果。

`数学解释：`

一般情况下都是绕X轴旋转的是pitch俯仰角，绕Y轴旋转的是yaw偏航角，绕Z轴旋转的是roll翻滚角。

最后，再让我们用数据公式来解释一下万向锁现象产生的原因，我们来回顾一下旋转矩阵：
在这里插入图片描述
这说明你改变φ和ψ的值都是一个效果，而矩阵的第一行和最后一列始终是保持不变，这说明无论你怎么改变φ和ψ，你的旋转轴一直是Z轴不变，要想改变φ和ψ有不同的效果，你只能是去改变θ的值，以上就是用数学方法来解释为什么俯仰角在±90°时欧拉角出现万向锁的过程。