本文主要是介绍用欧拉角表示旋转(方位)heading pitch bank 含义,形象的图示,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 简介

2. heading pitch bank 含义
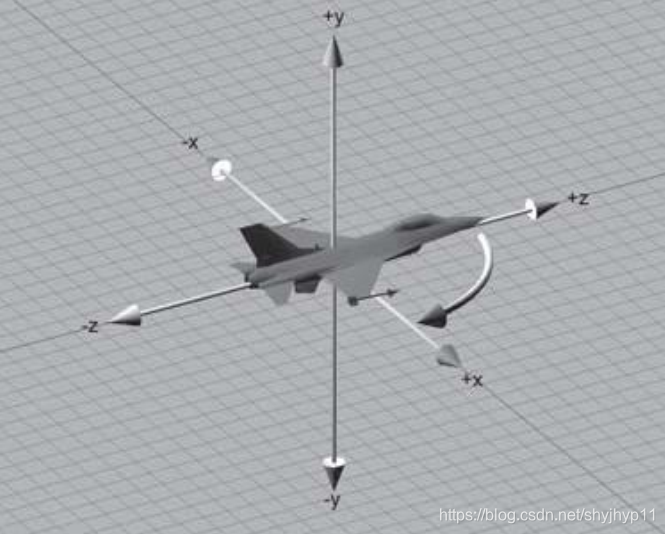
heading:
物体绕自身的对象坐标系的Y轴,旋转的角度,下图中,对象坐标系与场景坐标系是重合的。
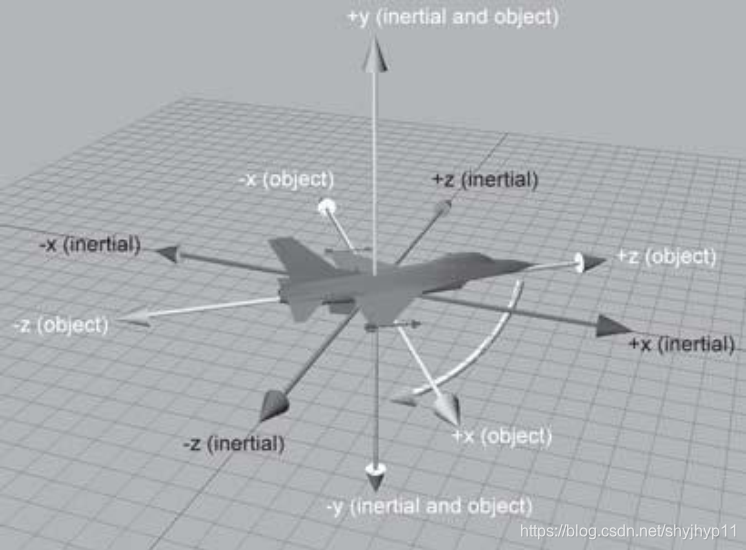
pitch:
物体绕自身的对象坐标系的X轴,旋转的角度,下图中,对象坐标系与场景坐标系未重合的。
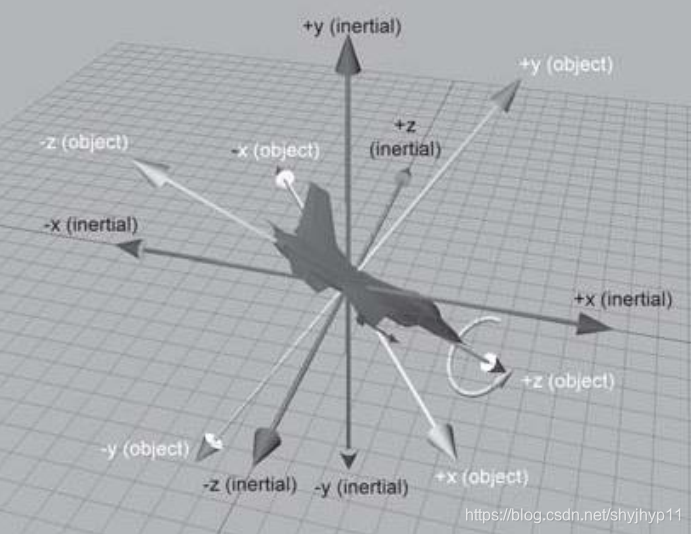
bank:
物体绕自身的对象坐标系的Z轴,旋转的角度,下图中,对象坐标系与场景坐标系未重合的。
3. 优缺点

规范化的欧拉角
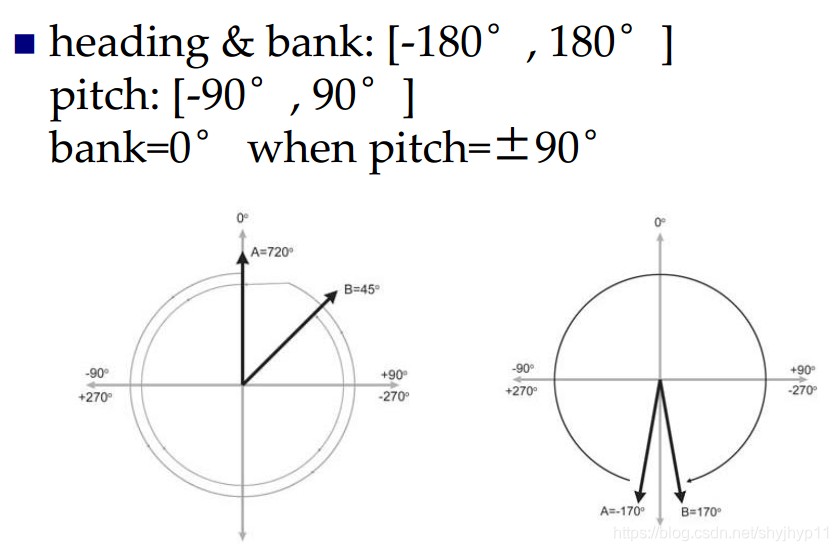
这篇关于用欧拉角表示旋转(方位)heading pitch bank 含义,形象的图示的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!