本文主要是介绍【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
专栏系列文章如下:
【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍
【视觉SLAM十四讲学习笔记】第二讲——初识SLAM
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
【视觉SLAM十四讲学习笔记】第三讲——Eigen库
本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动?
旋转向量
矩阵表示方式至少有一下两个缺点:
- SO(3)的旋转矩阵有9个量,但一次旋转只有3个自由度。因此这种表达方式是冗余的。同理,变换矩阵用16个量表达了6自由度的变换。
- 旋转矩阵自身带有约束:它必须是个正交矩阵,且行列式为 1。变换矩阵也是如此。当想要估计或优化一个旋转矩阵/变换矩阵时,这些约束会使得求解变得更困难。
因此,我们希望有一种方式能够紧凑地描述旋转和平移。例如,用一个三维向量表达旋转,用六维向量表达变换。事实上,任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量称为旋转向量(或轴角/角轴,Axis-Angle),只需一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的变量维数正好是六维。
考虑某个用R表示的旋转。如果用旋转向量来描述,假设旋转轴为一个单位长度的向量n,角度为 θ,那么向量 θn也可以描述这个旋转。
从旋转向量到旋转矩阵的转换过程由罗德里格斯公式(Rodrigues’s Formula )表明,转换的结果 :
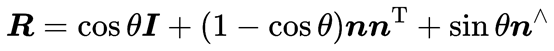
符号∧是向量到反对称矩阵的转换符。反之,我们也可以计算从一个旋转矩阵到旋转向量的转换。对于转角 θ,取两边的迹(矩阵对角线元素之和),有
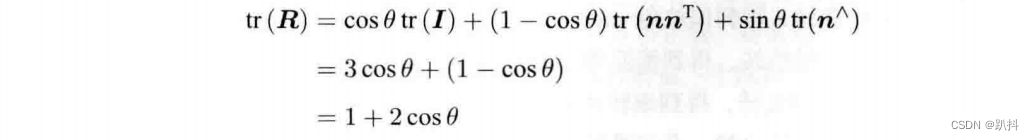
因此:
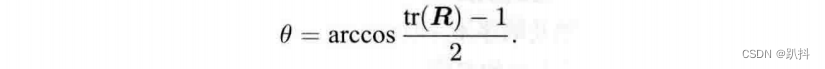
关于转轴n,由于旋转轴上的向量在旋转后不发生改变,说明:
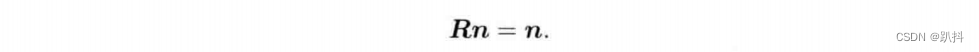
因此,转轴n是矩阵R特征值1对应的特征向量。求解此方程,再归一化,就得到了旋转轴。也可以从“旋转轴经过旋转之后不变”的几何角度看待这个方程。
欧拉角
无论是旋转矩阵、旋转向量,它们虽然能描述旋转,但对我们人类是非常不直观的。当我们看到一个旋转矩阵或旋转向量时,很难想象出这个旋转究竟是什么样的。当它们变换时,我们也不知道物体是向哪个方向在转动。而欧拉角则提供了一种非常直观的方式来描述旋转——它使用了3个分离的转角,把一个旋转分解成 3 次绕不同轴的旋转。而人类很容易理解绕单个轴旋转的过程。
但是,由于分解方式有许多种,所以欧拉角也存在着众多不同的、易于混淆的定义方法。比如说,先绕X轴旋转,再绕Y轴,最后绕Z轴,就得到了一个XYZ轴的旋转。同理,可以定义ZYZ、ZYX等旋转方式。如果讨论得更细一些,还需要区分每次是绕固定轴旋转的,还是绕旋转之后的轴旋转的。这种定义方式上的不确定性带来了很多实用当中的困难。
欧拉角当中比较常用的一种,便是用“偏航−俯仰−滚转”(yaw-pitch-roll)3个角度来描述一个旋转。它等价于ZYX轴的旋转。假设一个刚体的前方(朝向我们的方向)为X轴,右侧为Y轴,上方为Z轴。那么,ZYX转角相当于把任意旋转分解成以下3个轴上的转角:
-
绕物体的Z轴旋转,得到偏航角 yaw;
-
绕旋转之后的Y轴旋转,得到俯仰角 pitch;
-
绕旋转之后的 X 轴旋转,得到滚转角 roll。
此时,可以使用 [r,p,y]T 这样一个三维的向量描述任意旋转。
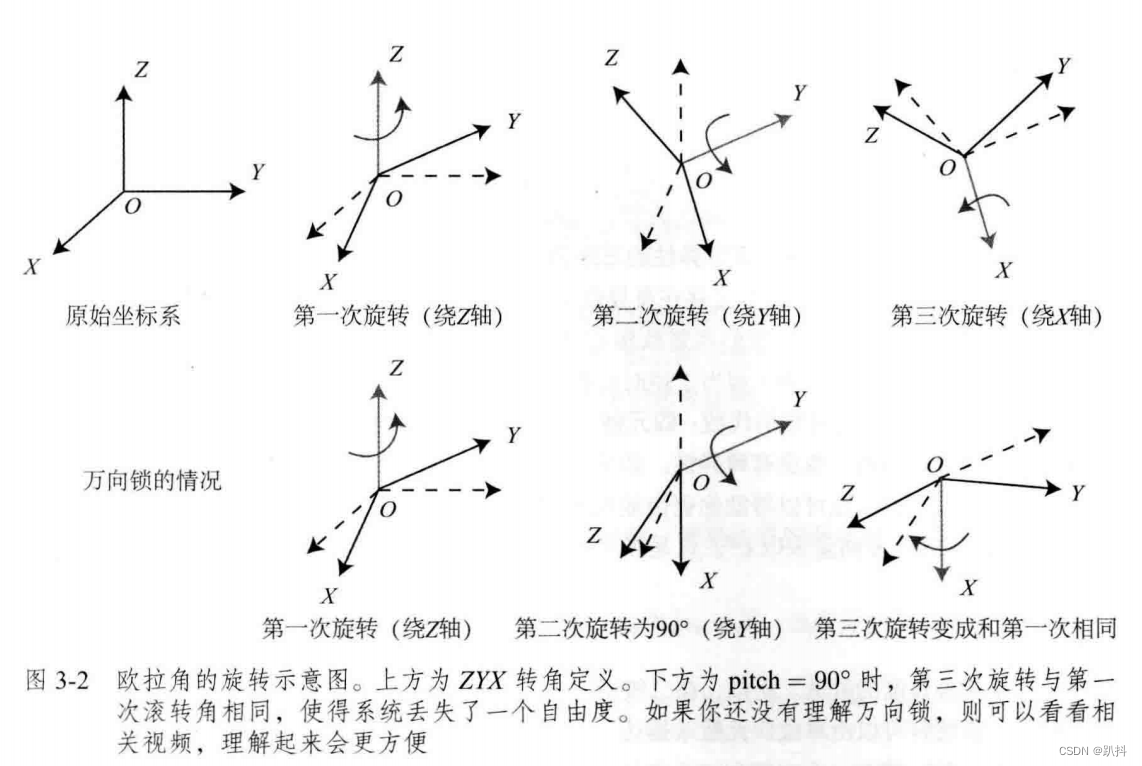
欧拉角的一个重大缺点是会碰到万向锁问题(Gimbal Lock ):在俯仰角为 ±90◦时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由 3 次旋转变成了 2 次旋转)。这被称为奇异性问题,只要想用3个实数来表达三维旋转时,都会不可避免地碰到奇异性问题(旋转向量也有奇异性,发生在转角θ超过2Π而产生周期性时)。
由于这种问题,欧拉角不适于插值和迭代,往往只用于人机交互中。我们很少在SLAM程序中直接使用欧拉角表达姿态,同样不会在滤波或优化中使用欧拉角表达旋转,因为它具有奇异性。如果想验证自己的算法是否有错,转换成欧拉角能够帮你快速分辨结果是否正确。
这篇关于【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








