本文主要是介绍数学概率 | 旋转矩阵、欧拉角、四元数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一,旋转矩阵
二维旋转矩阵
三维旋转矩阵
二,欧拉角
三,四元数
四,矩阵、欧拉角、四元数相互转换
四元数转矩阵
矩阵转四元数
欧拉角转矩阵
矩阵转欧拉角
欧拉角转四元数
四元数转欧拉角
一,旋转矩阵
二维旋转矩阵
R(
) =
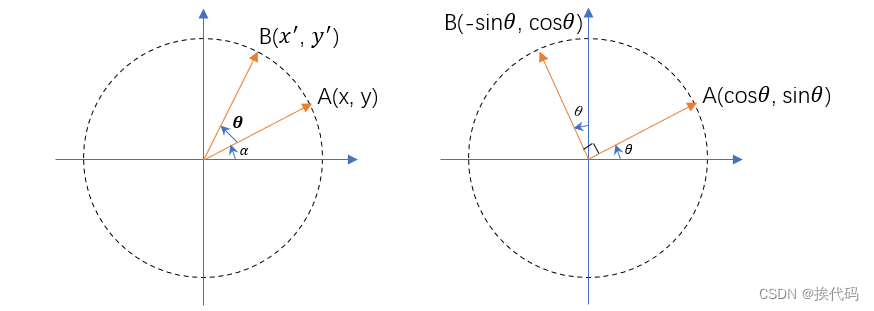
推导,以二维平面为例旋转
:
= cos(
+
) = cos
cos
- sin
sin
= cos
* x - sin
* y
= sin(
+
) = sin
cos
+ cos
sin
= sin
* x + cos
* y
(
,
) = (x , y) *
=(cos
* x - sin
* y ,sin
* x + cos
* y)
//Houdini vex 验证
matrix2 m = ch2('m');
vector2 p = set(@P.x, @P.y);
p *= m;@P.x = p.x;
@P.y = p.y;三维旋转矩阵
(
) =
(
) =
(
) =
参考二维推导,如绕z轴旋转
:
(
,
,z) = (x , y , z) *
= (cos
* x - sin
* y ,sin
* x + cos
* y , z)
注,已经过Houdini vex 验证;
二,欧拉角
欧拉角(Euler Angle),由著名数学家莱昂哈德·欧拉(1707-1783)提出,旨在用三个角度来表示刚体在三维空间的旋转,自身有一些局限性;
- 在坐标系中描述物体姿态的三个角,依据绕x轴Roll,绕y轴Pitch、绕z轴Yaw的三个角度旋转可还原描述的姿态;
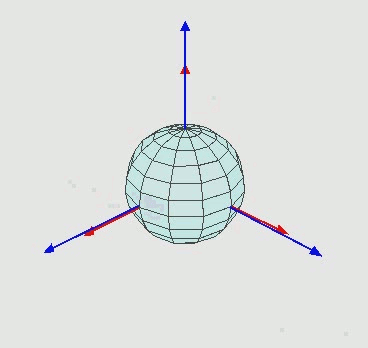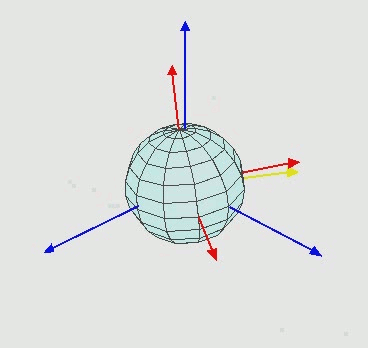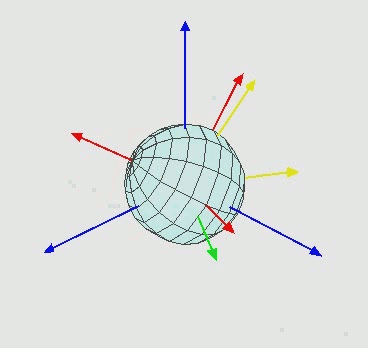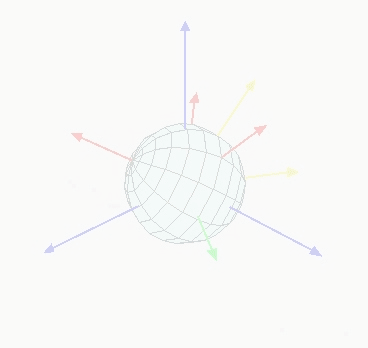

由两种旋转方式(静态、动态,这两种方式的所获得的旋转矩阵转是一样的:
- 绕固定(参考)坐标轴旋转(静态),绕自身坐标轴旋转(动态),旋转轴会发生变化,按照不同的旋转轴顺序,所获欧拉角也不同;
- 如绕固定(参考)坐标轴X-Y-Z旋转角度对应 (α,β,γ) ,绕自身坐标轴Z-Y-X旋转角度也对应 (α,β,γ),旋转矩阵为(注意坐标轴顺序):
注,已经过Houdini vex 验证;
如欧拉角在俯仰角出现±90°,会出现万向锁现象,是欧拉角表征姿态的一个固有缺陷;
在进行姿态解算时往往会优先使用四元数方法进行描述;
三,四元数
四元数是由爱尔兰数学家Hamilton发明的,由1个实数加上3个复数组合而成,通常可以表示成 w + xi + yj + zk 或者(w,(x,y,z)),其中w、x、y、z都是实数;
对于i、j、k本身的几何意义可以理解为一种旋转:
- i,旋转代表Y轴与Z轴相交平面中,Y轴正向向Z轴正向的旋转(
);
- j,旋转代表Z轴与X轴相交平面中,Z轴正向向X轴正向的旋转(
);
- k,旋转代表X轴与Y轴相交平面中,X轴正向向Y轴正向的旋转(
);
- -i、-j、-k分别代表i、j、k旋转的反向旋转;
q = w + xi + yj + zk
如绕某向量 K=(
,
,
) 旋转
,则四元数为:
- (x,y,z) = (
,
,
) *

- w =

- 且满足条件:
+
+
+
=1
注,已经过Houdini vex 验证,在vex内四元数为((x,y,z),w);
四,矩阵、欧拉角、四元数相互转换
四元数转矩阵
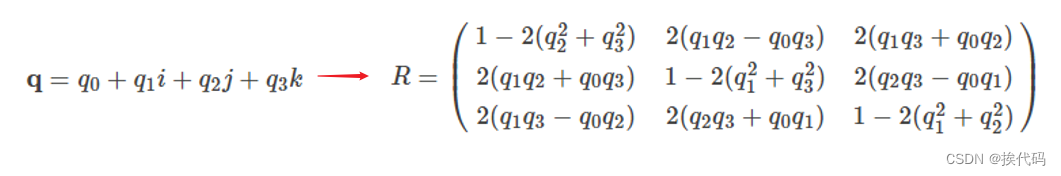
矩阵转四元数
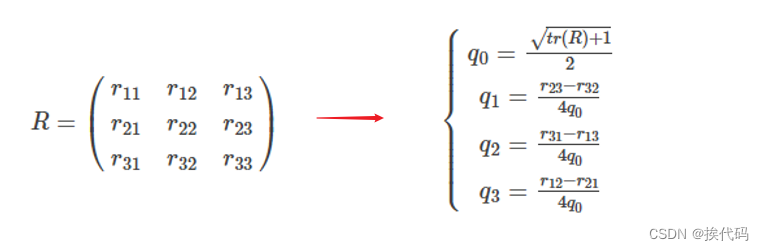
欧拉角转矩阵
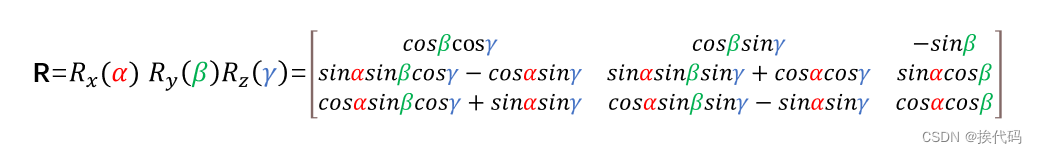
矩阵转欧拉角
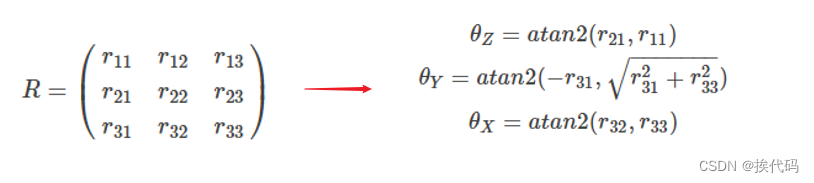
欧拉角转四元数
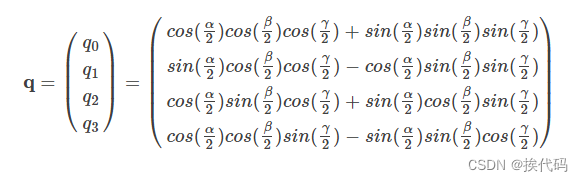
四元数转欧拉角

注:
- 欧拉角,直观易理解,存在万向锁问题;
- 旋转矩阵,不直观,计算复杂(尤其求微积分时);
- 四元数,不直观,但无奇点,能表征任何旋转关系,且表示简单,只有四个元素,计算量小;
这篇关于数学概率 | 旋转矩阵、欧拉角、四元数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






