神奇的四元数

神奇的四元数

来源视频: 四元数的可视化
顺便, 强烈推荐3b1b的视频

我们现在所熟知的向量，点乘、叉乘等，在四元数被发现时并不存在，至少没有标准化的形式。在当时，四元数被其他数学家认为是晦涩难懂的，他们认为没必要用这么复杂的东西来描述三维的变换。甚至据说，《爱丽丝梦游仙境》中的“疯帽子”就是隐射四元数的角色。

首先，我们之前就认识了虚数。复数是实数的二维延伸，四元数则是实数的思维延伸。

四元数则是有3个虚数轴，而第四个数，垂直于全部3个虚数轴。

四元数所描述的对四维空间的特殊作用与许多有着两种状态的量子系统有着紧密的联系。例如电子的旋转或者是光子的偏振。

四维右手法则：一旦理解了，就会对四元数乘法有一种自然而优美的直觉。

第一章 “直线人小莱”

小莱是一个直线人，它只知道实数的加减乘除，现在我们要向小莱介绍复数。在复平面上，横着的为实轴，竖着的为虚轴。

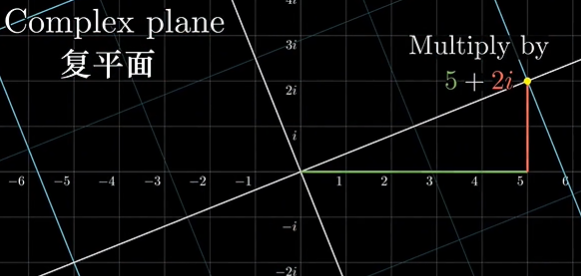
当复数相乘时，例如$$z\cdot w$$，把$$z$$想象成一个作用在$$w$$上的函数，它在对$$w$$做一些拉伸变换。
想象一个图钉把圆点固定住，然后用另一只手把1点拽到z点，因为0乘任何树都等于0，而1乘任何数都得到它本身，在二维世界中，有且只有一种拉伸旋转作用能做到这点。

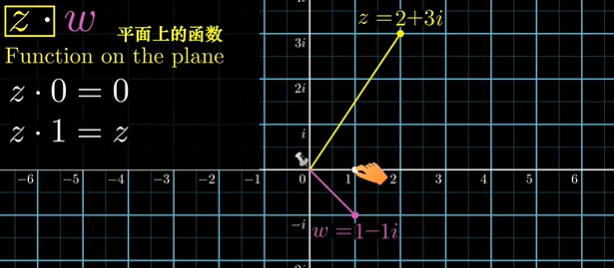
在拉伸的同时，坐标系也被你拉伸。

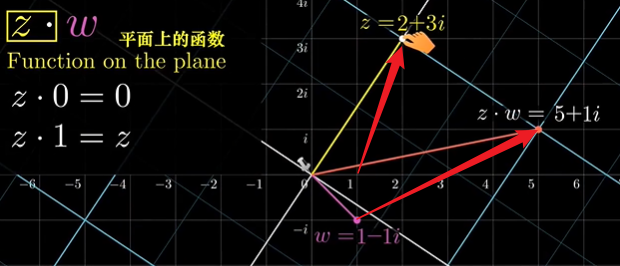
在复平面里，一个复数乘上单位圆上的向量，就是纯旋转。例如，我们拿i乘上任意复数w，在复平面上就是把这个复数w逆时针旋转90度。如果你将w乘i四次，它会等于它本身（这点在数学公式上也显而易见），而此时w其实已经逆时针转了一圈了。

第二章 “纸片人小菲”

纸片人小菲只能理解二维的世界，想象向小菲解释一个球体的旋转。
在复数的基础上，设定一个新的虚数j，j轴垂直于复平面。并且为了待会更好的理解四元数，我们让i轴和j轴分别坐落在x轴和y轴上。而实数轴则指向垂直于他们的位置。

三元数中的单位球

用“球极投影”将这个球投影到由i轴和j轴组成的水平面上。

球极投影：从（-1,0,0）发射出无数条直线，这些线经过球面，在i-j面上所映射的所有的点。

可想而知，单位球和i-j面相交的单位圆，是“小菲”能见到我们单位球上仅有的真实的那部分。

那么我们旋转这个单位球，在“小菲”眼里会是什么样的呢？

在上图中，黄圈代表着赤道投影的位置。

我们眼里立着的这个单位圆——越过1、i、-1、-i的单位圆，在“小菲”眼里就映射成了横轴。但这并不是i轴，这只是距离为1的点的投影，也就是说实际上是“间断的”。i轴上的大部分点，像0，2i，3i等则小菲完全见不到。
类似的，我们可以把j轴也映射出来。

那么，通过这种映射，在单位球上的任何点的旋转都可以被映射在i-j平面上了。
第三章 你，“三维人”

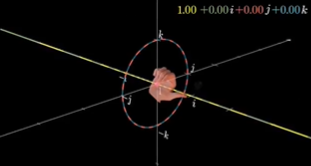
现在虚数又加了一个维度——k。i，j，k这三个虚数都和实数轴垂直，而且他们也互相垂直。

四元数可以由四个实数表示，并且它存在于四维空间中。

通过类比，思考一下四维超球……我们需要把四维超球“球极投影”到三维空间中来。

当我们把实部锁死为0，代表着四维超球投影到我们的空间中是不变的那部分。如同单位球相对于i-j平面的那样，这就是不变的部分。

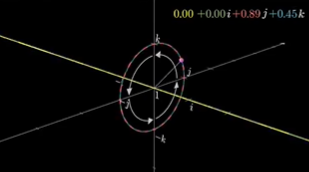
所有的四元数都有同样的模——1

正如我们在小菲的世界里投影出i轴，我们在这个世界里，看见i轴，要明白它其实是一个圆。同样的，在我们看不见的四维超球上，有一个单位三维球，通过1，i，j，-1，-i，-j，而整个球被投影到通过1，i，j，-i，-j以及无穷远处的-1的平面上，也就是我们说的x-y平面。

一个四位数左乘另一个四位数，也可以理解为一个函数。

之前的“旋转复数”在我们的眼里就是这个样子转了一圈。（只不过它到达过无穷远的地方，我们看不见这一段罢了。毕竟，我们是三维生物。）

四维空间右手定则

当你知道一个四元数对1，i，j，k做了什么，你就能理解这个四元数对其他四元数做了什么。

考虑同样的一个拖拽的过程，并且坐标系跟着一起动：