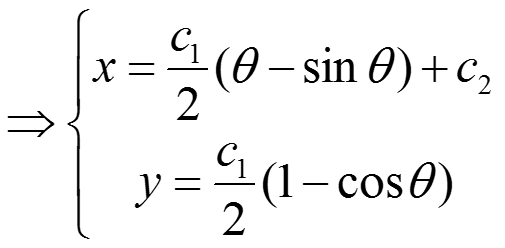lagrange专题

二次规划（Lagrange 方法，起作用集方法）

二次规划是非线性规划中一种特殊情形，它的目标函数是二次实函数，约束是线性的。由于二次规划比较简单，便于求解，且一些非线性规划可以转化为求解一系列二次规划问题，因此二次规划算法较早引起人们的重视，成为求解非线性规划的一个重要通径。二次规划的算法较多，本章介绍其中几个典型的方法，它们是 Lagrange 方法，起作用集方法，Lemke 方法和路径路踪法。一、Lagrange 方法考虑二次规划问

拉格朗日（Lagrange）插值曲线

简介拉格朗日（Lagrange）插值曲线是最简单的一种插值曲线。假设给定控制点（Xi, Yi）（i = 0,1,…,n），拉格朗日差值方法构造出一个不超过n次的插值多项式Pn(x)。得到的差值公式为：代码此段代码用于从一致的一系列控制点生成一系列点构成的插值曲线。 //xmax 为控制点中最大的横坐标//xmin 为控制点中最小的横坐标/

C#函数之实现Lagrange插值算法

博主最近想自己独立地完成一个精密单点定位的应用程序,先实现最简单的功能,那么基础工作就是要对igs最终的精密星历产品进行插值,以满足结算的要求,详细阐述请看前述文章:卫星位置插值方法简介(一) 博主在看过原理后，便使用C#进行了Lagrange函数的编写，话不多说先上代码： class interp{public double lagrange(List<double> T, List

Python数据分析与挖掘实战-Chapter6-lagrange插值

这本书实战是非常有借鉴作用的。尤其是这几个例子一步一步练下来还是非常有收获，但是我在运行原版程序的时候遇到一些问题，搜了一下全网，大家遇见的问题还是挺多的。可能是因为python编译器的版本迭代的问题。运行环境：vscode 1.61.0 / Python 3.8.8 / Anaconda 2.03 我在本章遇见的几个问题： 1- Scipy的Lagrange()函数结果有问题 2- 数

【数值计算方法（黄明游）】函数插值与曲线拟合（一）：Lagrange插值【理论到程序】

文章目录一、近似表达方式1. 插值（Interpolation）2. 拟合（Fitting）3. 投影（Projection）二、Lagrange插值1. 天书2. 人话拉格朗日插值方法a. 线性插值（n=1）基本思想线性插值与线性方程组 b. 抛物插值（n=2）基本思想优点和局限性应用场景 c. n次插值基本思想插值基函数的选择优点和和局限性 3. python实现4. C语言实

泛函与变分初步（Euler-lagrange条件）

1.前言若偏微分方程复杂或边界条件不规则时，则方程难以求得解析解，不得不求满足近似程度要求的近似解。变分法是常用的近似方法之一，而且，变分法的原理和应用遍及物理学的各个领域。所谓变分法即为泛函的极值问题。 2.泛函与泛函的极值 2.1 泛函的概念最速落径问题,如图所示。A、B两点不在同一铅垂线，也不在同一高度。一质点在重力作用下无磨擦沿某曲线从A滑到B，求下滑的最短时间。或沿

【优化】拉格朗日(Lagrange)乘子法超简说明

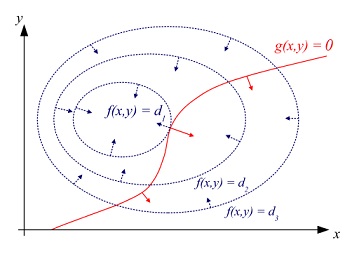
本文不做数学推导，从物理意义上讲解拉格朗日乘子法。原问题我们要解决带有等式约束的最优化问题。为方便书写，以二维函数为例： m a x f ( x , y ) , s . t . g ( x , y ) = 0 max\ f(x,y), \ \ s.t. g(x,y)=0 max f(x,y), s.t.g(x,y)=0 用下图表示这个问题。 f ( x ) f(x) f(x

lagrange dual problem

很高兴阿森纳能在欧冠上战胜拜仁，在虎扑上看到这样的一句话，颇有感触，借来作为这篇博文的开始，生活中我们需要一些勇气去追寻自己的理想。回到本篇内容上，对偶是个神奇的东西，从文学角度而言，对偶和对仗属于一种修辞手法，即用字数相等，语义对称的方法来表征想法或抒发情感。“凡心所向，素履所往，生如逆旅，一苇以航”或者“棋逢对手，将遇良才”都可看成是一种对偶。但是，本文是要阐述在数学问题上的对偶问题，它是

Python数据分析与挖掘实战-Chapter6-lagrange插值

这本书实战是非常有借鉴作用的。尤其是这几个例子一步一步练下来还是非常有收获，但是我在运行原版程序的时候遇到一些问题，搜了一下全网，大家遇见的问题还是挺多的。可能是因为python编译器的版本迭代的问题。运行环境：vscode 1.61.0 / Python 3.8.8 / Anaconda 2.03 我在本章遇见的几个问题： 1- Scipy的Lagrange()函数结果有问题 2- 数

约束优化之Lagrange乘子法KKT条件对偶问题最容易理解解读

1.无约束优化的常用方法在讲带约束优化方法之前，我们先简单回顾一下常用的无约束优化方法。 1.梯度下降法 2.牛顿法/拟牛顿法 3.共轭梯度法 … 上面梯度系列的无约束条件下的最优化，基本解法是根据极值的必要条件一阶导数为0，通过泰勒展开等形式，构造不同数列不断逼近最优解。 2.带约束的优化实际情况中，不带约束的场景比较少见，大部分都为带约束的优化问题。看一个大家都用的图：上图中，

理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

转自（http://blog.csdn.net/xianlingmao/article/details/7919597）在求取有约束条件的优化问题时，拉格朗日乘子法（Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法，对于等式约束的优化问题，可以应用拉格朗日乘子法去求取最优值；如果含有不等式约束，可以应用KKT条件去求取。当然，这两个方法求得的结果只是必要条件，

机器学习之拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

在求取有约束条件的优化问题时，拉格朗日乘子法（Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法，对于等式约束的优化问题，可以应用拉格朗日乘子法去求取最优值；如果含有不等式约束，可以应用KKT条件去求取。当然，这两个方法求得的结果只是必要条件，只有当是凸函数的情况下，才能保证是充分必要条件。KKT条件是拉格朗日乘子法的泛化。之前学习的时候，只知道直接应用两个方法，但是却

PlonK Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge学习笔记-1

PLONK 课程笔记最近在看plonk，直接看论文有些吃力，在哔哩哔哩上观看课程讲解，很细致https://www.bilibili.com/video/BV1XZ4y1A7bU?share_source=copy_web 1. plonk的基本原理 1.将数学运算化为多项式，之后再化为电路。 2.多项式承诺（手上的一堆多项式，满足一定的关系：证明方发送给验证者，承诺发出后，多项式不可

【学习笔记】插值之拉格朗日插值（Lagrange）

0 插值介绍插值法是广泛应用于理论研究和工程实际的重要数值方法。用提供的部分离散的函数值来进行理论分析和设计都是极不方便的，因此希望能够用一个既能反映原函数特征，又便于计算的简单函数去近似原函数。 1 低次拉格朗日插值定理：设 x 0 {x_0} x0, ⋯ {\cdots} ⋯, x n {x_n} xn是互异插值节点，则满足差值条件 p ( x i ) = y i ( i = 0

Lagrange与KKT的简易解释

本文将以梯度下降法的方式来解释Lagrange和KKT。关键词：梯度下降法、等高线基础定义 Lagrange 求解等式约束下的最优化问题 Lagrange函数： (1) 方程组的解是原问题的可能的最优解 KKT 求解不等式约束下的最优化问题 Lagrange函数： (2) 方程组，即KKT条件，的解是原问题的可能的最优解解释梯度的定义，等式约束因

$优化问题的拉格朗日Lagrange对偶法原理$

优化问题的拉格朗日Lagrange对偶法原理

首先我们定义一般形式的求解x的优化问题：表示优化的目标函数，上述为最小优化，实际上最大优化可以改写为的形式表示第i个不等式约束表示等式约束 1. Lagrange对偶问题上述优化问题的拉格朗日Lagrange对偶法求解，是将上述带约束的目标优化问题改写为如下无约束的Lagrange函数式子。上述Lagrange函数式子存在如下对偶函数，其是Lagrange函数关于取最小值，即

拉格朗日c语言实验报告,拉格朗日（Lagrange）插值法（C语言）

题目拉格朗日插值法流程图 (1)二次插值： #include float lagelangri(float x[],float y[],float xx,int n) { int i,j; float *a,yy=0; a=new float[n]; for(i=0;i<=n-1;i++) { a[i]=y[i]; for(j=0;j<=n-1;j++) if(j!=i)a[i]*=(xx

数值分析——多项式插值之Lagrange插值

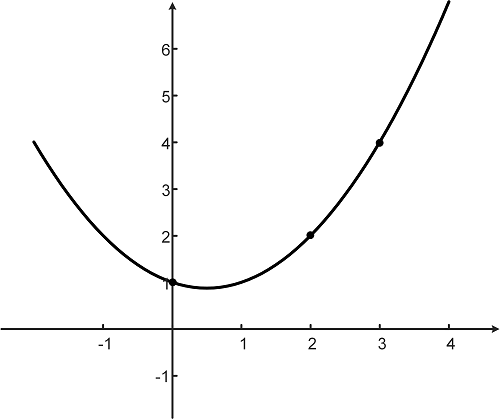
一、引言　　考虑这样一个实际例子，当我们按下计算器的正弦按钮时，会发生什么？我们都知道计算器有可以处理加法和乘法的硬件，但是，它是如何计算一个数的正弦值呢？多项式插值法就可以解决这样的问题。我们将在未来重新审视这个问题。目前，我们先来学什么是插值以及如何插值。二、什么是插值　　如下图所示，假定我们收集了一组数据点$(x, y)$，譬如$(0, 1), (2, 2), (3, 4)$。有一条

[转]数值分析——多项式插值之Lagrange插值

一、引言　　考虑这样一个实际例子，当我们按下计算器的正弦按钮时，会发生什么？我们都知道计算器有可以处理加法和乘法的硬件，但是，它是如何计算一个数的正弦值呢？多项式插值法就可以解决这样的问题。我们将在未来重新审视这个问题。目前，我们先来学什么是插值以及如何插值。二、什么是插值　　如下图所示，假定我们收集了一组数据点(x,y)(x,y)(x, y)，譬如(0,1),(2,2),(3,4)(0,

Lagrange duality拉格朗日对偶性

Welcome To My Blog 在约束最优化问题(Constrained Optimization)中,常常利用拉格朗日对偶性(Lagrange duality)将原始问题转换为对偶问题,通过求解对偶问题而得到原始问题的解,该方法可用在最大熵模型(Maximum Entropy)和支持向量机(Support Vector Machine). 约束最优化问题标准形式: f(x),

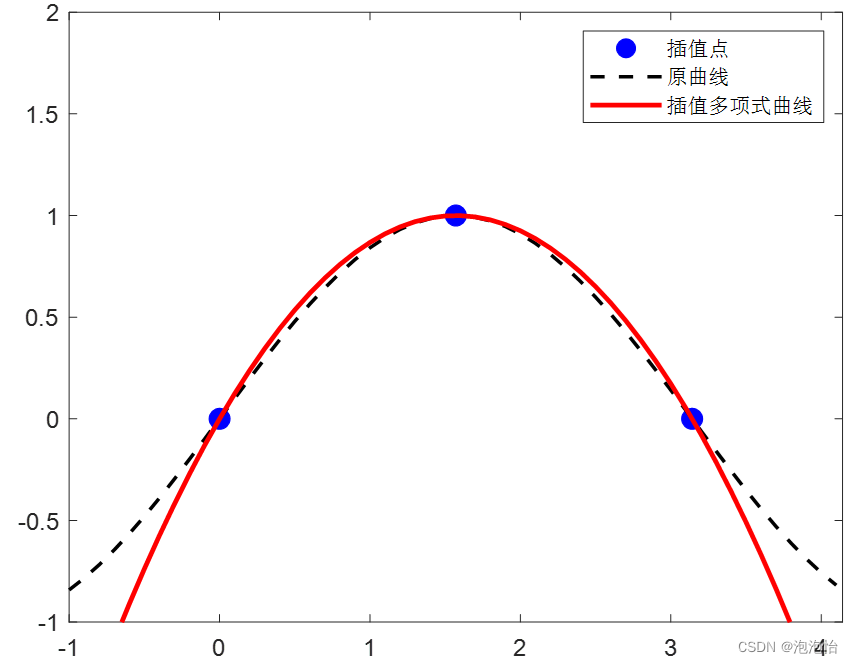
Lagrange 拉格朗日插值 | matlab实现

function y_p = Lagrange(x, y, x_p)% x为插值节点的横坐标% y为插值节点的纵坐标% x_p 为需计算的插值函数值的横坐标% y_p 为插值函数值num_poly = length(x); % 多项式的项数y_p = []num = length(x_p); % 要计算的插值函数值的个数for j = 1:nump = 0;for i = 1:num

插值余项 + 高次插值的Runge现象 | Lagrange拉格朗日插值（二）

1. 插值余项用Lagrange插值公式计算除插值节点以外的某一插值点x处的值，其插值误差为： R n ( x ) = f ( x ) − p n ( x ) R_n(x)=f(x)-p_n(x) Rn(x)=f(x)−pn(x) 该误差实际上就是截断误差，称 R n ( x ) R_n(x) Rn(x)为Lagrange插值的插值余项。定理2：设 x 0 , x 1 , ⋯ ,

任意一点X0到超平面S的距离以及拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

转自： http://blog.csdn.net/xinzaichenmo/article/details/70161728 http://blog.csdn.net/xianlingmao/article/details/7919597 在求取有约束条件的优化问题时，拉格朗日乘子法（Lagrange Multiplier) 和KKT条

$Lagrange插值函数及其Matlab代码$