一、引言
考虑这样一个实际例子,当我们按下计算器的正弦按钮时,会发生什么?我们都知道计算器有可以处理加法和乘法的硬件,但是,它是如何计算一个数的正弦值呢?多项式插值法就可以解决这样的问题。我们将在未来重新审视这个问题。目前,我们先来学什么是插值以及如何插值。
二、什么是插值
如下图所示,假定我们收集了一组数据点$(x, y)$,譬如$(0, 1), (2, 2), (3, 4)$。有一条经过这三点的抛物线,我们把这条抛物线称为经过这3点的二次插值多项式。
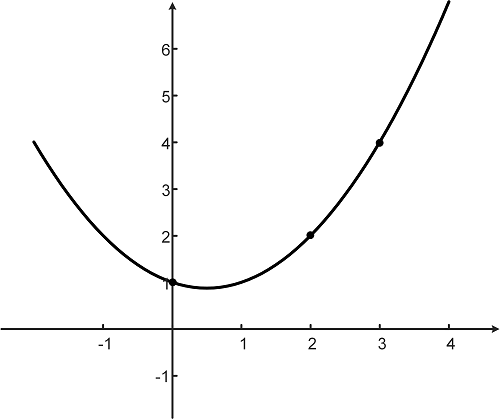
这样就引出了插值的数学定义,如下:
【插值的定义】 如果$P(x_i) = y_i (1 \leqslant i \leqslant n)$,那么函数$y = P(x)$插值了数据点
$(x_1, y_1), \cdot \cdot \cdot , (x_n, y_n)$
简单来讲就是,如果一个函数通过了一组数据点,那么就称这个函数插值了这组数据点。
二、Lagrange插值
2.1 讨论
现在我们知道了什么是插值,请大家考虑一个问题,如果我只知道一组n个数据点$(x_1, y_1), \cdot \cdot \cdot , (x_n, y_n)$,我们想要求出一个多项式,能够插值这一组所有的数据点。并且这个多项式的次数是$d = n - 1$次的,该怎么做?
Lagrange插值公式给出了这个问题的解答方案。例如,假设给定点$(x_1, y_1), (x_2, y_2), (x_3, y_3)$,那么其2次插值多项式可以由Lagrange插值多项式给出,如下:
$P_2(x) = y_1 \frac{(x - x_2)(x - x_3)}{(x_1 - x_2)(x_1 - x_3)} + y_2 \frac{(x - x_1)(x - x_3)}{(x_2 - x_1)(x_2 - x_3)} + y_3 \frac{(x - x_1)(x - x_2)}{(x_3 - x_1)(x_3 - x_2)}$
那么有人可能会问,这样的多项式一定是正确的吗,答案是:是的。我们可以验证一下:
1. 当$x = x1$时,$P_2(x1) = y1$;
2. 当$x = x2$时,$P_2(x2) = y2$;
3. 当$x = x3$时,$P_2(x3) = y3$;
我们只考虑这三个点,因为我们只有这三个点,在这3个点上,这个多项式都成功的插值了,因此,这个多项式一定是正确的。(注意这个多项式关于变量$x$是2次的)
2.2 数学定义
一般地,假设给出$n$个点$(x_1, y_1), \cdot \cdot \cdot , (x_n, y_n)$,则对于1和n之间的每一个$k$可定义
$L_k(x) = \frac{(x - x_1) \cdot \cdot \cdot (x - x_{k -1})(x - x_{k + 1}) \cdot \cdot (x - x_n)}{(x_k - x_1) \cdot \cdot \cdot (x_k - x_{k -1})(x_k - x_{k + 1}) \cdot \cdot (x_k - x_n)}$
$L_k$的一个有趣性质是:
1. $L_k(x_k) = 1$
2. $L_k(x_j) = 0 \qquad (j \neq k)$
因此,定义$n - 1$次Lagrange多项式
$P_{n - 1}(x) = y_1 L_1(x) + \cdot \cdot \cdot + y_n L_n(x)$
2.3 存在性和及唯一性
有人会问,对于给定的n个数据点,其插值多项式是唯一的吗?即只能是由一个多项式才能插值这n个点吗?答案是:不是。
大家想想就知道,对于二维平面的$n$个坐标点,我们肯定能画出无穷条线来穿过这些点,每一条线都对应这一个多项式。那么这个问题的意义何在?
多项式是无穷的,但是,对于插值$n$个数据点的多项式,其最高次数是小于等于$n - 1$的,这样的多项式,只能是只有一个。用数学来描述这个问题如下:
【定理】
设$(x_1, y_1), \cdot \cdot \cdot, (x_n, y_n)$是平面上$x_i$互不相同的$n$个点,那么存在一个而且仅存在一个次数小于等于$n - 1$次的多项式,满足
$P(x_i) = y_i, \qquad i = 1, \cdot \cdot \cdot, n$
【证明】
(1) 存在性:存在性已由Lagrange插值的显式公式得出。
(2) 唯一性:假定有存在两个这样公式,譬如$P(x)$及$Q(x)$,它们最多是$n - 1$次,而且都插值所有$n$个点,即有:
$P(x_1) = Q(x_1) = y_1, P(x_2) = Q(x_2) = y_2, \cdot \cdot \cdot, P(x_n) = Q(x_n) = y_n$。
则有$H(x) = P(x) - Q(x)$,显然,$H$的次数最多也是$n - 1$,而且注意到
$H(x_1) = H(x_2) = \cdot \cdot \cdot = H(x_n)$
即$H$有$n$个不同的零点。按照代数学基本定理,一个$d$次多项式,除了它恒等于零多项式,最多可能有$d$个零点。因此有
$H \equiv 0$
于是,
$P(x) \equiv Q(x)$
因此,存在唯一的次数小于等于$n - 1$的多项式$P(x)$插值与$n$个点$(x_i, y_i)$。
2.4 范例
【题目】求插值于点$(0, 2), (1, 1), (2, 0), (3, -1)$的次数小于等于3的多项式。
【解】Lagrange形式如下:
$P(x) = 2 \frac{(x - 1)(x - 2)(x - 3)}{(0 - 1)(0 - 2)(0 - 3)} + 1 \frac{(x - 0)(x - 2)(x - 3)}{(1 - 0)(1 - 2)(1 - 3)} + 0 \frac{(x - 0)(x - 1)(x - 3)}{(2 - 0)(2 - 1)(2 - 3)} + (-1) \frac{(x - 0)(x - 1)(x - 2)}{(3 - 0)(3 - 1)(3 - 2)} = -x + 2$





