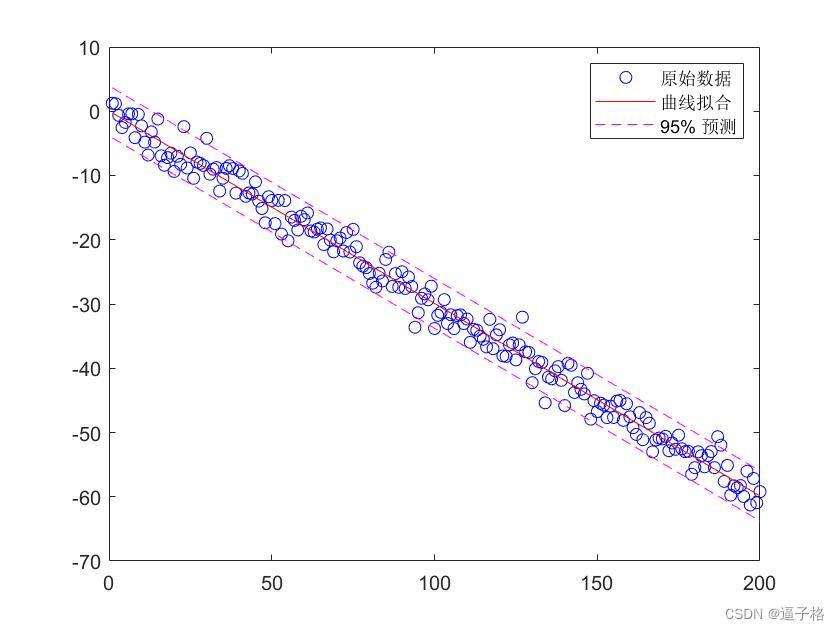
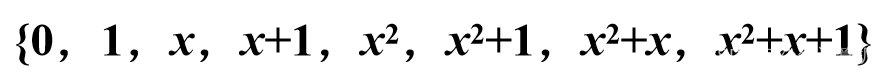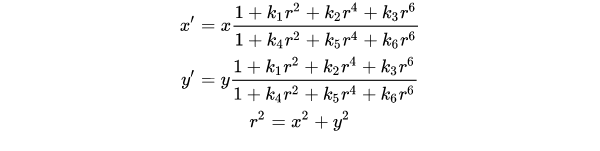多项式专题
算法笔记02--归纳法之多项式求值(Horner规则)
多项式求值 假设有n+2个实数a0,a1,...,an和x的序列,求多项式 p_nx = a_nx^n + a_n-1x^n-1 + ...+ a_1x + a_0; 则需要乘法:n+n-1 + ...+2+1 = n(n+1)/2 需要加法:n 可见算法效率为O(n^2) 而p_nx = ((...((((a_n)x + a_n-1)x + a_n-2)x + a_n-3)....)
链表(篇5)用链表实现多项式相加
使用链接实现两个多项式相加 例: 输入:第一数= 5x ^ 2 + 4x ^ 1 + 2x ^ 0第二数= 5x ^ 1 + 5x ^ 0输出:5x ^ 2 + 9x ^ 1 + 7x ^ 0输入:第一数= 5x ^ 3 + 4x ^ 2 + 2x ^ 0第二数= 5x ^ 1 + 5x ^ 0输出:5x ^ 3 + 4x ^ 2 + 5x ^ 1 + 7x ^ 0 代码
【机器学习】基扩展的基本概念以及其中的多项式回归、样条方法和广义可加模型的简单介绍(含python代码实例)
引言 基扩展是提升模型性能的重要工具,正确选择和应用基扩展方法可以显著提高模型的预测能力和解释性 文章目录 引言一、基扩展1.1 基扩展定义1.2 基扩展方法1.2.1 多项式基扩展1.2.2 样条基扩展1.2.3 径向基函数(RBF)1.2.4 傅里叶基扩展1.2.5 wavelet基扩展1.2.6 单隐藏层神经网络 1.3 应用场景1.4 使用基扩展的注意点 二、多项式回归2.
约瑟夫环和一元多项式
约瑟夫环 一、问题描述 假设有 n 个人围成一圈,从第一个人开始报数,报数到 m 的人将被淘汰出圈,然后从下一个人开始继续从 1 报数,如此重复,直到最后只剩下一个人。求最后剩下的这个人的编号。 二、问题分析 可以使用循环链表来模拟这个过程。 1.创建一个包含 n 个节点的循环链表,每个节点代表一个人,节点中存储这个人的编号。 2.从第一个节点开始报数,每报到 m,就将对应
采用不高于3次的勒让德多项式拟合原函数
利用勒让德多项式进行拟合的区域是[-1,1],如果不是这个区域,比如是[a,b],利用转化到[-1,1]。 参考以下例题计算系数 C语言代码如下 //用三阶的勒让德多项式进行拟合#include<math.h>#include<stdio.h>#include "main.c"double f(double x);double fl1(double x);double f
回归分析系列19— 多项式回归进阶
24 多项式回归进阶 24.1 简介 多项式回归是一种扩展线性回归的方法,用来建模非线性关系。通过将输入变量升至多项式次幂,可以捕捉数据中的非线性特征。虽然模型复杂度增加,但也带来了更高的拟合能力。然而,过高次幂的多项式可能会导致过拟合问题。 24.2 多项式特征的构建 在多项式回归中,我们首先需要生成多项式特征,即将原始特征升至不同次幂并组合。Python中的scikit-learn库提
03-1. 二分法求多项式单根(20) MOOC
二分法求函数根的原理为:如果连续函数f(x)在区间[a, b]的两个端点取值异号,即f(a)f(b)<0,则它在这个区间内至少存在1个根r,即f(r)=0。 二分法的步骤为: 检查区间长度,如果小于给定阈值,则停止,输出区间中点(a+b)/2;否则如果f(a)f(b)<0,则计算中点的值f((a+b)/2);如果f((a+b)/2)正好为0,则(a+b)/2就是要求的根;否则如果f((a+b)
基于Python的机器学习系列(10):朴素贝叶斯 - 多项式模型
在之前的文章中,我们已经探讨了朴素贝叶斯分类器在不同情况下的应用。本文将继续深入探讨,重点介绍朴素贝叶斯分类器中的多项式模型。 1. 背景介绍 朴素贝叶斯分类器是一种基于贝叶斯定理的简单却强大的分类算法。在之前的文章中,我们介绍了高斯朴素贝叶斯模型,它假设特征服从高斯分布。然而,对于一些特定类型的数据,例如词频或计数数据,高斯分布并不是最合适的选择。这时,我们可
机器学习算法(二):1 逻辑回归的从零实现(普通实现+多项式特征实现非线性分类+正则化实现三个版本)
文章目录 前言一、普通实现1 数据集准备2 逻辑回归模型3 损失函数4 计算损失函数的梯度5 梯度下降算法6 训练模型 二、多项式特征实现非线性分类1 数据准备与多项式特征构造2 逻辑回归模型 三、逻辑回归 --- 正则化实现1 数据准备2 逻辑回归模型3 正则化损失函数4 计算损失函数的梯度5 梯度下降6 训练模型 总结 前言 今天我们开始介绍逻辑回归的从零开始实现代码了,
【C++实验】多项式加减
题目:一元多项式运算 基本要求: (1) 输入并建立多项式; (2) 输出多项式; (3) 多项式加法 (4) 多项式减法。 测试数据: 代码展示: #include<iostream>using namespace std;class LinkedNode{public:LinkedNode(double COEF, doub
AI学习指南机器学习篇-多项式朴素贝叶斯算法简介
AI学习指南机器学习篇-多项式朴素贝叶斯算法简介 前言 随着人工智能技术的快速发展,机器学习作为其中的一个重要分支已经成为各个领域的热门话题。而在机器学习算法中,朴素贝叶斯算法因其简单易懂、效果不俗而备受青睐。本文将针对多项式朴素贝叶斯算法展开详细介绍,包括原理、应用、优缺点分析等内容,帮助读者更好地理解和运用这一经典的机器学习算法。 多项式朴素贝叶斯算法的原理 多项式朴素贝叶斯算法是一种
多元多项式的特征列与零点的关系定理
下面这个定理来自《计算机代数》6.1三角列与特征列(王东明、夏壁灿著) 【定理】 设 C = [ C 1 , … , C r ] \mathbb{C =}\left\lbrack C_{1},\ldots,C_{r} \right\rbrack C=[C1,…,Cr]为多项式组 P ⊂ K [ x ] \mathbb{P \subset}\mathcal{K\lbrack}\mathbf
1071: 数据结构作业01 -- 一元多项式的求积
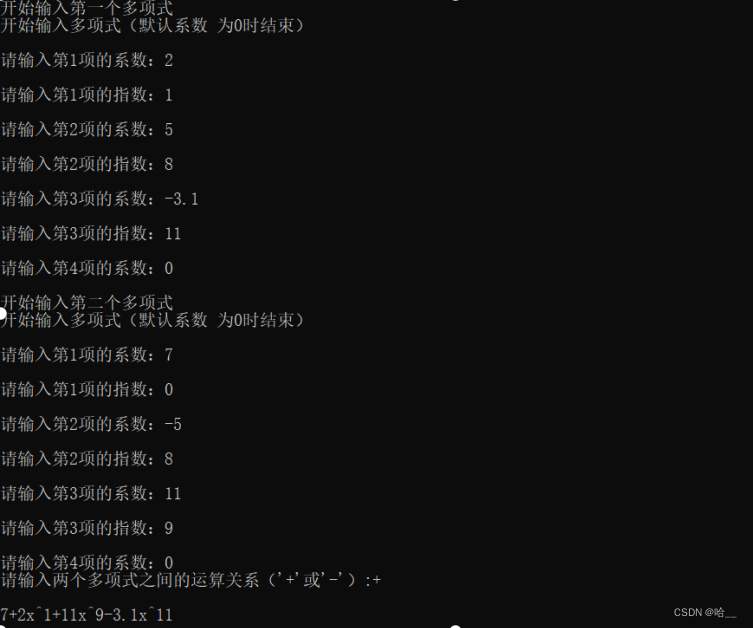
1071: 数据结构作业01 -- 一元多项式的求积 时间限制: 1 Sec 内存限制: 128 MB 提交: 48 解决: 8 [ 提交][ 状态][ 论坛] 题目描述 一个一元多项式可以看作由若干个一元单项式按降幂排列成的线性表。请编写程序对输入的两个一元多项式求积,并输出求积的结果。 输入 输入为两个一元多项式,每个一元多项式输入一行,按照降幂依次输入每个
Plonky3和Binius中的Brakedown多项式承诺协议解析及优化(2)
3. Breakdown Commitment 3.1 Linear Codes Polynomial Commitments Breakown的基础就是使用线性码构建多项式承诺,优点在于证明大小和验证时间复杂度都是长度的平方根。 下面给出一个简单的线性码多项式承诺过程。假设多项式 g g g的系数向量的长度为 n n n,并且可以使用填充0的方式扩充到 d = k 2 d=k^2 d=k2
算法金 | 一个强大的算法模型,多项式回归!!
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 吴恩达:机器学习的六个核心算法!–> 线性回归 在许多实际场景中,简单的线性回归无法捕捉复杂的模式,这时候就该祭出我们多项式回归大法了,一种在数据分析和预测中常用的机器学习方法。 本文的目的在于为大侠们提供多项式回归的基础理解,并通过代码示范和数据可视化,展示如何在实
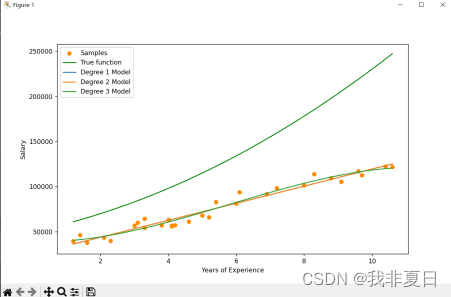
分别利用线性回归、多项式回归分析工资与年限的关系
一、线性回归: 实验思路: 先分析线性回归的代码,然后结合Salary_dataset.csv内容分析,编写代码。 实验代码: import pandas as pdimport numpy as npfrom sklearn.linear_model import LinearRegressionfrom sklearn.metrics import mean_squar
网络空间安全数学基础·多项式环与有限域
5.1 多项式环(掌握) 5.2 多项式剩余类环(理解) 5.3 有限域(熟练) 5.1 多项式环 定义:设F是一个域,称是F上的一元多项式. 首项:如果an≠0,则称 anx^n 为f(x)的首项 次数:n是多项式f(x)的次数,记为deg(f(x)) = n 首一多项式:如果an = 1,则称f(x)为首一多项式 零次多项式:若f(x) = a0≠0,则约定deg(f(x)) = 0 F上
MOOC 数据结构 | 2. 线性结构(4):应用实例:多项式加法运算
4. 多项式加法运算 主要思路:相同指数的项系数相加,其余部分进行拷贝。 4.1 多项式相加在计算机中的实现 上述多项式用单向链表表示: (每个结点包含系数,指数和指向下一个结点的指针) 4.2 数据结构定义 struct PolyNode{int coef; //系数int expon;//指数struct PolyNode *link; //指向下一个结点的指针};t
FZU - 2115 多项式积分
题意: Description 给定一个关于x(小写字母)的多项式,求其关于x的一阶积分,结果按降幂输出,要求结果为最简多项式。输出的多项式符合一般书写规则,即有如下特性: 多项式由单项式相加或相减组成,单项式可以表示成ax^b的形式,其中a、b均为整数,b为大于等于0的整数,a不能为0,特别的,当b等于1时,省略”^1”,写做ax,当b等于0时,写作a,而当a的值为±1时,1必须省略。多项
26、matlab多项式曲线拟合:polyfit ()函数
1、polyfit 多项式曲线拟合 语法 语法:p = polyfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数,该阶数是 y 中数据的最佳拟合(基于最小二乘指标)。 语法:[p,S] = polyfit(x,y,n) 还返回一个结构体 S 语法:[p,S,mu] = polyfit(x,y,n) 执行中心化和缩放以同时改善多项式和拟合算法的数值属性。 参数 x:查询点 y
rqn 516 多项式输出(字符串输出处理)
题目连接:http://www.rqnoj.cn/Problem_516.html 解题思路:分类考虑一下。 1、第一个'+'不用输出; 2、系数为1不输出; 3、幂为1不输出; 4、系数为0整项不输出。 #include <stdio.h>#include <string.h>#include <stdlib.h>const int N = 105;int main() {i
一元多项式的相加、相乘
#define null 0 #include "stdio.h" #include "stdlib.h" #include "math.h" typedef struct { float coef;//系数 int expn;//指数 }term;//代表一元多项式的一项 typedef struct Lnode { term data;//链表的一个结点存放一项 Lnode * ne
【鱼眼镜头11】Kannala-Brandt模型和Scaramuzza多项式模型区别,哪个更好?
Kannala-Brandt模型和Scaramuzza多项式模型在描述鱼眼相机畸变时都有其特定的数学表示和应用,但它们之间存在一些区别。以下是对两者区别的分点表示和归纳: 数学表示: Kannala-Brandt模型:它假设图像光心到投影点的距离和角度的多项式存在比例关系。具体地,它涉及到相机坐标系、图像坐标系、物点坐标、入射角、畸变像点和非畸变像点等参数,并通过这些参数之间的关系来描述径向畸
洛谷 P3803 【模板】多项式乘法(FFT)
【模板】多项式乘法(FFT) 题目背景 这是一道多项式乘法模板题。 注意:本题并不属于中国计算机学会划定的提高组知识点考察范围。 题目描述 给定一个 n n n 次多项式 F ( x ) F(x) F(x),和一个 m m m 次多项式 G ( x ) G(x) G(x)。 请求出 F ( x ) F(x) F(x) 和 G ( x ) G(x) G(x) 的卷积。 输入