分别利用线性回归、多项式回归分析工资与年限的关系

本文主要是介绍分别利用线性回归、多项式回归分析工资与年限的关系，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、线性回归：

实验思路：

先分析线性回归的代码，然后结合Salary_dataset.csv内容分析，编写代码。

实验代码：

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt# 1. 读取数据
data = pd.read_csv('Salary_dataset.csv')# 假设数据是干净的，没有缺失值或异常值
X = data['YearsExperience'].values.reshape(-1, 1)  # 特征列
y = data['Salary'].values  # 目标变量列# 2. 选取五个数据点作为训练集
# 这里我们随机选取五个数据点，你可以根据需要更改选取数据点的方式
train_indices = np.random.choice(len(data), 5, replace=False)
X_train = X[train_indices]
y_train = y[train_indices]# 剩余的数据作为测试集
X_test = np.delete(X, train_indices, axis=0)
y_test = np.delete(y, train_indices, axis=0)# 3. 训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)# 4. 评估模型
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_pred)print(f'Mean Squared Error: {mse}')
print(f'Root Mean Squared Error: {rmse}')
print(f'R² score: {r2}')# 5. 可视化结果
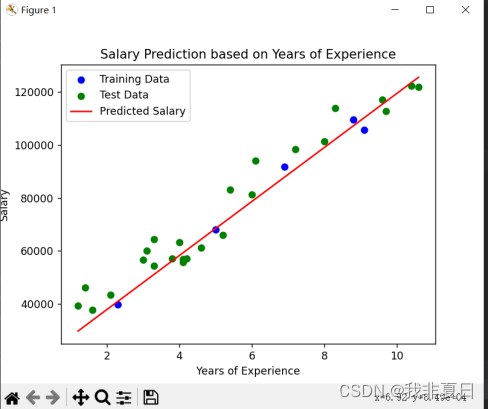
plt.scatter(X_train, y_train, color='blue', label='Training Data')
plt.scatter(X_test, y_test, color='green', label='Test Data')
plt.plot(X_test, y_pred, color='red', label='Predicted Salary')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.title('Salary Prediction based on Years of Experience')
plt.legend()
plt.show()

实验结果：

二、多项式回归：

实验思路：

先分析多项式回归的代码，然后结合Salary_dataset.csv内容分析，编写代码。

实验代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression# 读取CSV文件
data = pd.read_csv('Salary_dataset.csv')
X = data['YearsExperience'].values.reshape(-1, 1)  # 特征
y = data['Salary'].values  # 目标变量# 假设的真实函数（这里只是一个例子，实际上我们不知道真实函数）
def true_function(x):return 50000 + 8000 * x + 1000 * x ** 2  # 假设的真实工资与年限关系# 创建X值的范围用于绘制真实函数和模型预测
X_plot = np.linspace(X.min(), X.max(), 100).reshape(-1, 1)
y_true = true_function(X_plot)# 定义多项式次数
degrees = [1, 2, 3]# 初始化图表和子图
plt.figure(figsize=(10, 6))
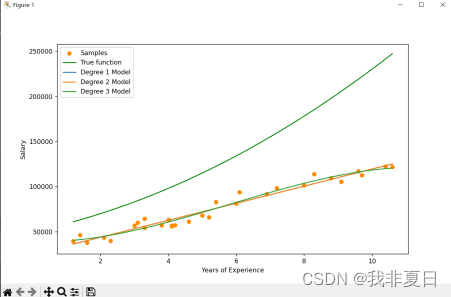
plt.scatter(X, y, color='darkorange', label='Samples')  # 绘制样本点
plt.plot(X_plot, y_true, color='green', label='True function')  # 绘制真实函数
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.legend(loc='upper left')# 对每个多项式次数进行训练和可视化
for i, degree in enumerate(degrees):polynomial_features = PolynomialFeatures(degree=degree, include_bias=False)linear_regression = LinearRegression()pipeline = Pipeline([("polynomial_features", polynomial_features),("linear_regression", linear_regression)])pipeline.fit(X, y)# 使用管道进行预测y_plot = pipeline.predict(X_plot)# 绘制模型拟合曲线plt.plot(X_plot, y_plot, label=f'Degree {degree} Model')# 显示图例
plt.legend(loc='best')
plt.show()