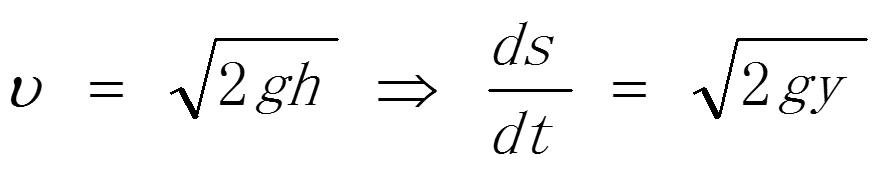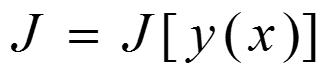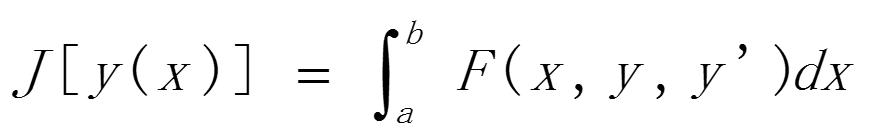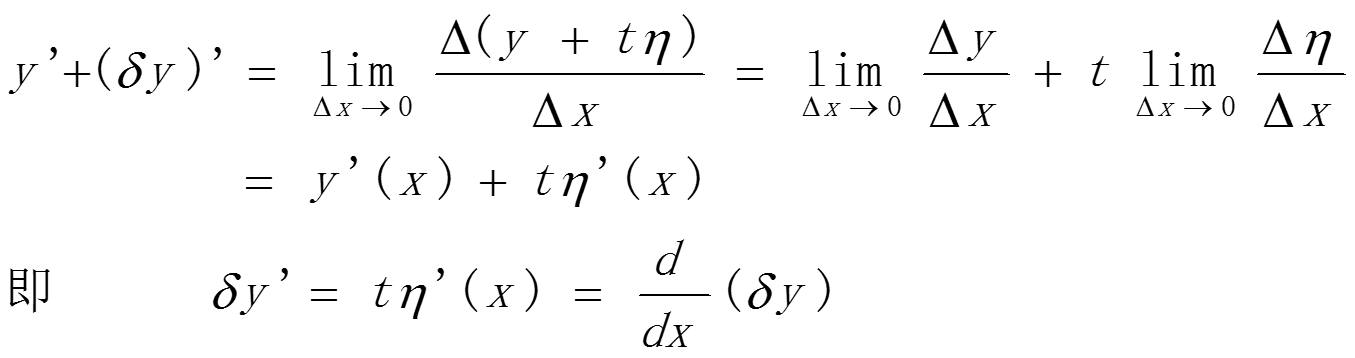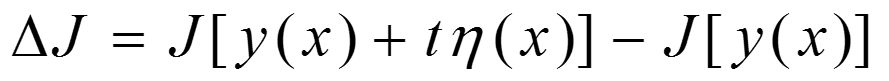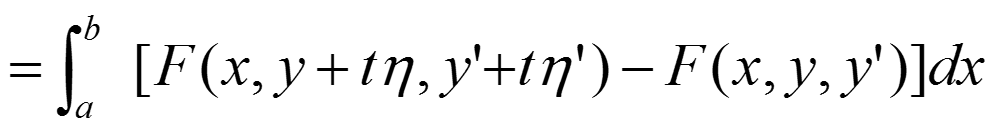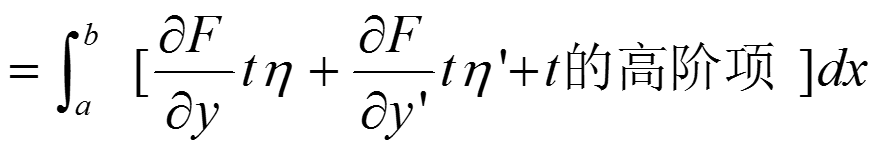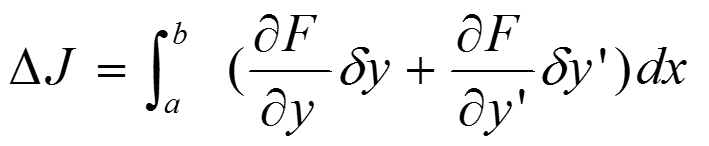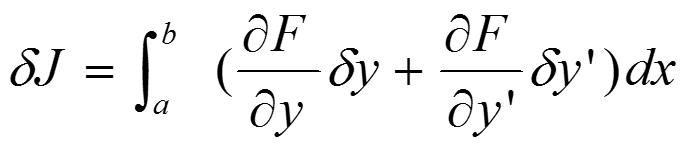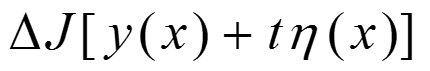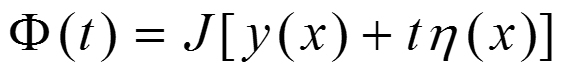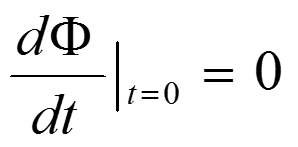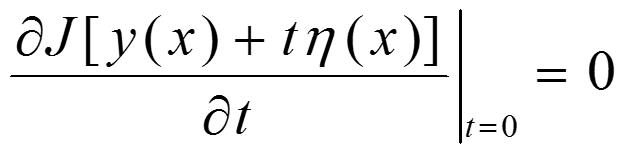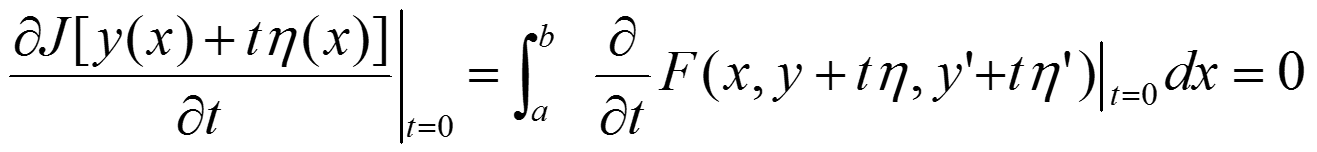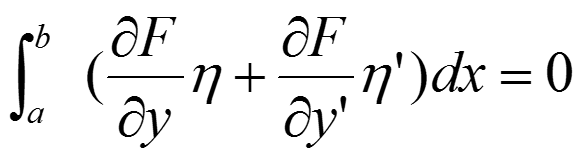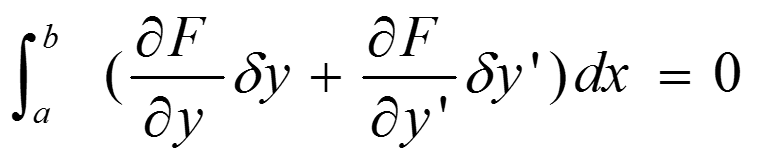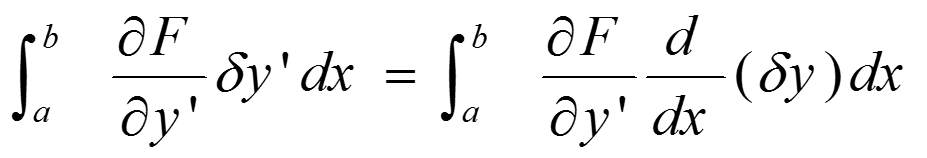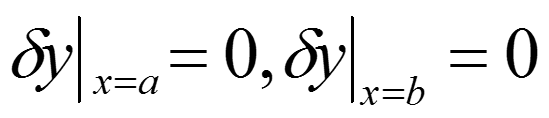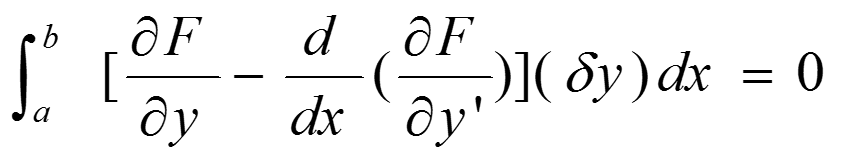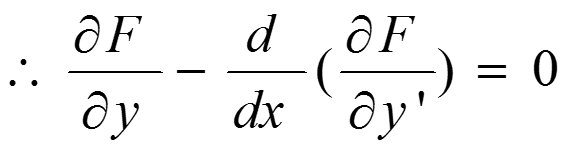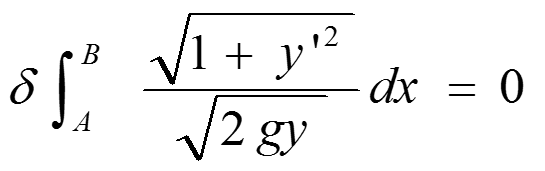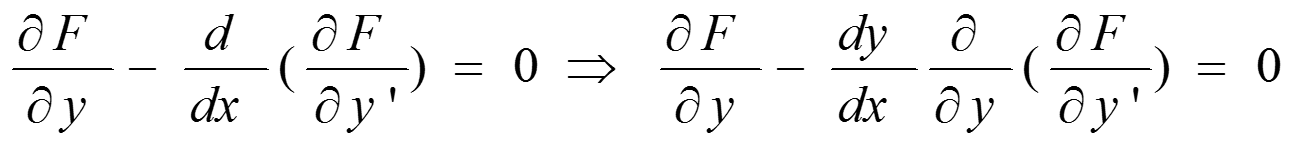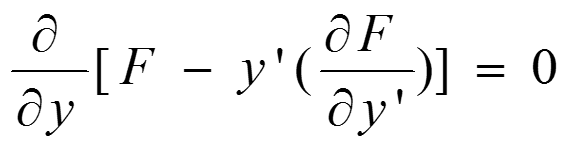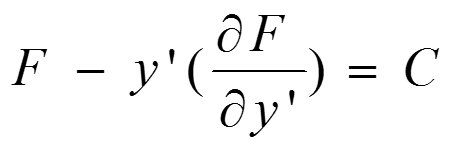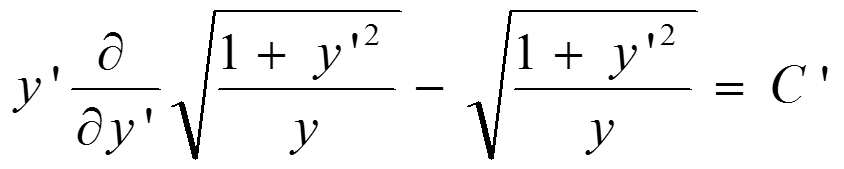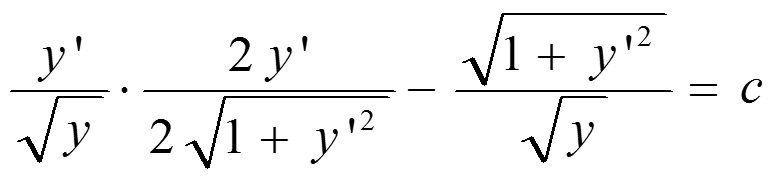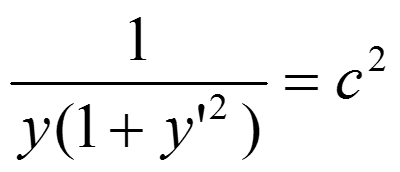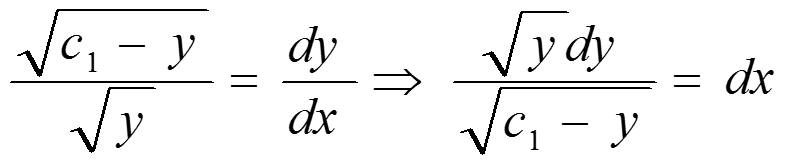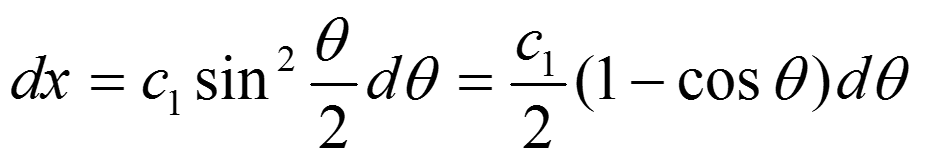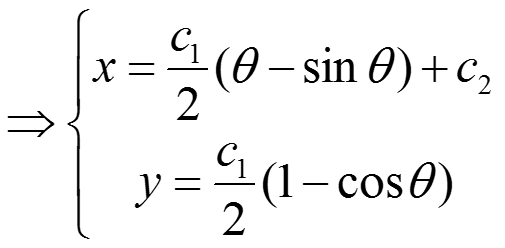泛函与变分初步（Euler-lagrange条件）

若偏微分方程复杂或边界条件不规则时，则方程难以求得解析解，不得不求满足近似程度要求的近似解。变分法是常用的近似方法之一，而且，变分法的原理和应用遍及物理学的各个领域。所谓变分法即为泛函的极值问题。

2.泛函与泛函的极值

2.1 泛函的概念

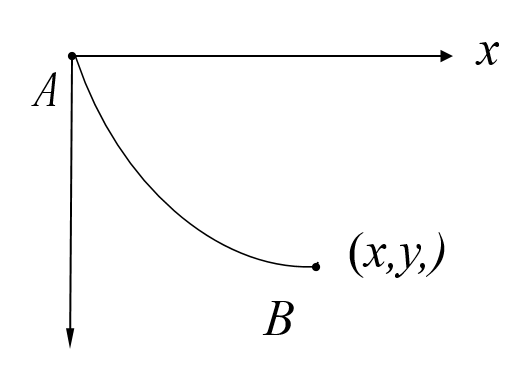
最速落径问题,如图所示。A、B两点不在同一铅垂线，也不在同一高度。一质点在重力作用下无磨擦沿某曲线从A滑到B，求下滑的最短时间。或沿哪条曲线用时最短。

我们知道，质点下落速率与下落高度间的关系为：

所以

即T称为y(x)的泛函。

y(x)可取的函数种类，称泛函的定义域,泛函是函数的函数（不指复合函数）。

一般地， C是函数的集合， B是实数（或复数）的集合，若对于C中的任一称元素y(x) ，在B中均有一元素J与之对应，则称J为y(x) 的泛函是函数。

记为：

与通常函数的定义不同，泛函的值决定于函数的取形。如上例中，T的变化决定于y(x)的变化，而非某一个自变量x的值进而某一个函数y的值。而是决定于函数集合C中的函数关系，即决定于函数的取形。

通常，泛函多以积分形式出现，如：

其中，F(x,y,y`)称为泛函的核。

2.2泛函的极值与变分

在泛函的概念下，最速落径问题归结为泛函T[y(x)]的极值问题，所谓变分法,就是求泛函的极值问题。研究泛函极值问题的方法归为两类：直接法与间接法。要讨论间接法，先讨论泛函的变分问题。

设有连续函数y(x)，将其微小变形为y(x)+tn(x)。

其中t是一个小参数，tn(x)称为y(x)的变分，记为δy。

此时，函数y`(x)相应变形为：

导数的变分等于变分的导数,变分微分运算可交换次序。

设中F(x,y,y`)二阶可导，y``连续！如果函数y(x)存在变分δy时，泛函J的变化为：

相对于y、y’作Tayler展开，抵消t的0次项，保留t的1次项，略去t的高阶项。

可得：

上式称泛函 J [y（x）]第一次变分！！！简称变分，记为：

3.泛函极值的必要条件——欧拉方程

设泛函 J [y（x）]的极值问题有解，记为y = y(x)；现在来推导此解y（x）满足的常微分方程。

设y=y（x）有变分δy=tn(x)， 则

可视为t的函数。

表示为：

这样，就把原来的泛函的极值问题转变成这种普通函数的极值问题。 

令：

即：

将代入上式，得：

即：

同乘t 得：

泛函取极值的必要条件是其变分为0，或者说，泛函J的极值函数y(x)必须是满足泛函的变分dJ=0的函数类。所以泛函的极值问题称为变分问题。

又因为：

根据分部积分公式可以知道：

在简单变分问题中，端点是固定的：

所以可以得到：

这就是变分学中大名鼎鼎的“欧拉-朗格朗日条件”！！！

欧拉(Euler)方程是泛函有极值的必要条件。

4.经典最速落径问题求解

根据引言一节，最速路径问题用泛函描述为：

解：由于 欧拉方程变形为 ：

提取公共部分，可得：

简化为：

代入原方程，得：

求出偏导数得：

通分，并取平方可得

取.y(1+y`*y`)=c1,得：

令代入上式可得：

因此，我们就可以得到摆线得参数方程：

常数c1 、c2由A、B位置决定。

5.参考资料

1.钱伟长. 变分法及有限元[M]. 科学出版社, 1980.

2.郭大钧. 非线性泛函分析-第2版[M]. 山东科学技术出版社, 2001.