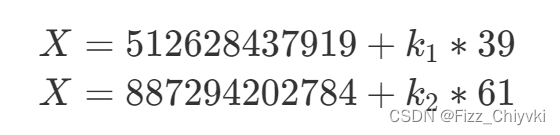euler专题
【UVa】 10735 Euler Circuit 混合图的欧拉回路 最大流
题目链接:http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1676 题目要求:求混合图的欧拉回路+输出路径。 题目分析: 先看一段比较流行的说法吧~: -----------------------------------------
BCLinux Euler 21.10 安装mysql 8.0.37 (二进制安装)
下载mysql安装包 #根据ldd --version的信息, 下载的是glic 2.28的包。下载地址:https://downloads.mysql.com/archives/community/包名:mysql-8.0.37-linux-glibc2.28-x86_64.tar.xz #root用户操作#系统环境:BigCloud Enterprise Linux For E
车辆姿态角(Euler角)Pitch、Yaw、Roll 的设定
首先申明:此坐标系是针对车辆而设定的,对于无人机来说是不同的。 pitch():俯仰角,pitchAngleC2W (orientation radian Y) yaw():航向角,yawAngleC2W (orientation radian Z) roll():横滚角,rollAngleC2W (orientation radian X)
Project Euler 92
Square digit chains Problem 92 A number chain is created by continuously adding the square of the digits in a number to form a new number until it has been seen before. For example, 44 → 32
project euler problem 35求一个数的所有循环数都是素数的总共有多少个
这题刚开始想到的是怎么求出这些循环数,然后求出来以后判断就容易多了。但是刚开始想的是用取模和相除的求出的循环数,但是有点麻烦,而且程序总有点问题,所以我就想了另外的一个思路。以前记得做题的时候有道题也是关于循环数的,而循环数可以先把它变成字符串,然后这个字符串再连接自己的字符串,如:15234,连接后为:1523415234,然后就可以知道这些循环数了,即第二个数为从第二位取5个数为:52341,
求解常微分方程初值问题之多步Euler预报-校正法
//实现多步Euler法 #include <iostream> #include <math.h> #include <iomanip> using namespace std; class multi_euler { private: int i, n; double f, h, x, x_last, yc, yc_old, yp; public: double func(doub
UVA 1342 - That Nice Euler Circuit(计算几何+欧拉定理)
大白上的例题 思路:首先要知道欧拉定理, 顶点数V,边数E,面数F,那么有V + F - E = 2 那么剩下就是根据已有的图形,计算出有多少个顶点和多少条边,就能计算出面数了 于是暴力计算几何搞搞即可 代码: #include <cstdio>#include <cstring>#include <cmath>#include <algorithm>using namesp
VMware虚拟机安装Open Euler
1、请先安装vmware,如不会可站内搜索 2、openeula安装 step1 镜像下载 openEuler | 开源社区 | openEuler社区官网https://www.openeuler.org/zh/ 选择合适的版本,最后那个是网络安装 step2 在vmware安装 打开vmwar
Euler 筛法(欧拉筛法)
筛法 - OI Wiki 埃氏筛法很好理解,素数的倍数都是合数,做标记不筛即可。 但是2和3都能筛到6,12,18,等,会重复标记。 欧拉筛理解: 筛选 n 以内的素数,存入vector<int>pri 中。 not_prime标记合数。 # 埃氏筛是给 质数 乘以 每个 i,得出所有倍数。 # 这里给 每个 i 乘以 质数 如果自己是这个质数的倍数,就结束,就避免了重复。
Euler's Totient Function(欧拉函数)
定义 欧拉函数 ϕ(n)=count(p),p∈[1,n] AND gcd(p,n)=1 \phi(n)=count(p),p\in[1,n]\ \mathrm{AND} \ gcd(p,n)=1,其中 count(p) count(p)表示满足上述条件 p p的数目。公式ϕ(n)=n∏p|n(1−1p)\phi(n)=n\prod_{p|n}(1-\dfrac{1}{p}) 其中, p p
Project Euler_Problem 160_Factorial Trailing Digits_费马小定理,威尔逊定理,左右互搏
原题目: 题目大意:1e12的阶乘,不算末尾的0,后5位数字为多少 解题思路: 暴力运算也能算,就是有点慢,优化过后可能也得算个几十分钟 这里考虑使用威尔逊定理+费马小定理 用这个方法我们就可以得到对于任何一个小于p的数n,p为素数,n!在模p下的结果, 对于本题: 则我们要找的答案应该是512628437919+k*39的最后几位有效数字,当k>100000时,显然末尾数字就
Project Euler_Problem 172_Few Repeated Digits_动态规划
原题目: 题目大意:18位数里头,有多少个数,对于每个数字0-9,在这18位里面出现均不超过3次 111222333444555666 布星~~ 112233445566778899 可以~~ 解题思路: 动态规划 代码: ll F[19][3000000];void solve() {ll i, j,k,x,y,z,p,q,u,v;ll N = 18,NN=4;double
Project Euler 题解 #45 Triangular, pentagonal, and hexagonal
题目:Triangular, pentagonal, and hexagonal Triangle, pentagonal, and hexagonal numbers are generated by the following formulae: Triangle Tn=n(n+1)/2 1, 3, 6, 10, 15, ...Pentagonal Pn=n(3n1)/2 1, 5, 12
Project Euler 题解 #20 Factorial digit sum
题目:Factorial digit sum n! means n (n 1) ... 3 2 1 For example, 10! = 10 9 ... 3 2 1 = 3628800, and the sum of the digits in the number 10! is 3 + 6 + 2 + 8 + 8 + 0 + 0 = 27. Find the sum of the di
Project Euler 题解 #40 Champernowne's constant
题目:Champernowne's constant An irrational decimal fraction is created by concatenating the positive integers: 0.123456789101112131415161718192021... It can be seen that the 12th digit of the fraction
Project Euler 题解 #19 Counting Sundays
题目:Counting Sundays You are given the following information, but you may prefer to do some research for yourself. 1 Jan 1900 was a Monday.Thirty days has September, April, June and November. All the
Project Euler 题解 #11 Largest product in a grid
题目:Largest product in a grid In the 2020 grid below, four numbers along a diagonal line have been marked in red. 08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08 49 49 99 40 17 81 18 57 6
Project Euler 题解 #18 #67 Maximum path sum
题目:Maximum path sum I Maximum path sum II By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23. 3 7 4 2 4 6 8 5
Project Euler 题解 #16 Power digit sum
题目:Power digit sum 215 = 32768 and the sum of its digits is 3 + 2 + 7 + 6 + 8 = 26. What is the sum of the digits of the number 21000? 这个题目在于大数乘法以及减枝。 数学描述 首先有个结论,如下: 那么,N = 21000时,C(N)=30
2017 多校7 1005 Euler theorem
http://acm.hdu.edu.cn/showproblem.php?pid=6124 找出一个数对所有的正整数取余的不同结果的数量, 是有规律的,把前10个写出来就可以看出来了 偶数:n/2+1 奇数:(n+1)/2+1; #include<iostream>using namespace std;int main(){int t;
数学分析复习:圆周率和 Euler 常数的构造
文章目录 圆周率 π \pi π 和 Euler 常数 e e e 的构造圆周率 π \pi π 的构造Euler常数e的构造 本篇文章适合个人复习翻阅,不建议新手入门使用 圆周率 π \pi π 和 Euler 常数 e e e 的构造 圆周率 π \pi π 的构造 我们将以下数列的极限定义为 π \pi π L n = n ⋅ sin 18 0
矩阵Matrix到欧拉角Euler转换
参考文献: http://www.geometrictools.com/Documentation/EulerAngles.pdf 但是这里的公式不能直接用,原因是左右手系空间不同,我这边采用Direct3D默认的右手系,参考: https://docs.microsoft.com/en-us/windows/win32/direct3d9/d3dxmatrixrotationyawpitc
13、弗罗莱(Fleury)算法,求欧拉(Euler)通路/回路
1、基本概念: (1)定义 欧拉通路 (欧拉迹)—通过图中每条边一次且仅一次,并且过每一顶点的通路。 欧拉回路 (欧拉闭迹)—通过图中每条边一次且仅一次,并且过每一顶点的回路。 欧拉图—存在欧拉回路的图。欧拉图就是从一顶出发每条边恰通过一次又能回到出发顶点的那种图,即不重复的行遍所有的边再回到出发点。 通路和回路-称vie1e2…envj为一条从 vi到 vj且长度为n的通路,其中长度
Project_Euler-42 题解
Project_Euler-42 题解 题目 思路 开辟一个二维数组,一维存放单词,二维存放每个单词的字符串。然后去遍历每一个一维数组,求价值,判断,记录。 代码 #include <stdio.h>#include <stdlib.h>#include <math.h>#include <string.h>#include <time.h>#include "./E
Project_Euler-42 题解
Project_Euler-42 题解 题目 思路 开辟一个二维数组,一维存放单词,二维存放每个单词的字符串。然后去遍历每一个一维数组,求价值,判断,记录。 代码 #include <stdio.h>#include <stdlib.h>#include <math.h>#include <string.h>#include <time.h>#include "./E
Project_Euler-13 题解
Project_Euler-13 题解 题目 371072875339021027987979982208375902465101357402504637693767749000971264812489697007805041701826053874324986199524741059474233309513058123726617309629919422133635741615